Схема и описание установки

Диэлектрическую проницаемость твердых диэлектриков можно определить, измеряя сопротивление плоского конденсатора переменному току. Принципиальная схема установки представлена на рис. 1.2.

Переменное напряжение от генератора поступает на плоский конденсатор С, между пластинами которого помещается образец из диэлектрика. Сила переменного тока, текущего через конденсатор, измеряется амперметром, напряжение на обкладках конденсатора – вольтметром. Ёмкостное сопротивление конденсатора можно найти по закону Ома:

. (1.8)

Далее, зная ёмкостное сопротивление конденсатора, из (1.9)

(1.9)

можно определить ёмкость:

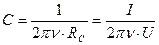. (1.10)

Учитывая, что и (D – диаметр обкладок конденсатора, d – расстояние между ними) для относительной диэлектрической проницаемости из (1.10) получим:

,

или

. (1.11)

Порядок выполнения работы

1. Ознакомьтесь с приборами и принципом действия измерительной установки.

2. Измерьте линейкой диаметр D обкладки конденсатора.

3. Измерьте микрометром толщину d исследуемых образцов. Запишите результаты в табл.1.1.

4. Приподняв верхнюю обкладку конденсатора, вставьте исследуемый образец между обкладками.

5. На генераторе ГЗ-118 установите произвольную частоту из диапазона от 50^.10² Гц до 80^.10³ Гц.

6. На миллиамперметре нажмите кнопку «2». При этом предел измерения тока будет равен 2 миллиамперам, а результат индицируется в микроамперах. Включите приборы в сеть.

7. Рассчитайте цену деления вольтметра. Предел измерения вольтметра составляет 12 В. Измерения следует снимать по шкале вольтметра, помеченной «VA~» (вторая снизу шкала). Установите напряжение, даваемое генератором, в пределах 6÷10 В.

8. Запишите в таблицу 1.1 частоту ν генератора, напряжение U и силу тока I. При необходимости измените предел измерения амперметра до 200 микроампер, нажав кнопку «200»; при этом результат даётся в микроамперах.

9. Изменяя частоту и/или напряжение, сделайте ещё 2÷4 измерения с данным образцом.

Таблица 1.1

D =……м
№	Материал образца	d, м	n, Гц	Dn, Гц	U, В	Δ U, В	I, А	Δ I, А	e	e СР.	D e
	Стекло
	Оргстекло
	Текстолит
	Пенопласт

10. Вычислите по формуле (1.11) значение e для исследуемого образца.

11. Рассчитайте среднее значение для данного материала, оцените погрешность.

12. Все результаты запишите в табл.1.11.

13. Замените образец. Повторите измерения по пунктам 5÷12. Проделайте измерения не менее чем для трех образцов.

14. Сравните полученные результаты с табличными, сделайте выводы.

 

Кон­троль­ные во­про­сы

1. Чем обу­слов­ле­на и как про­ис­хо­дит по­ля­ри­за­ция ди­элек­три­ков в элек­три­че­ском по­ле?

2. Дай­те оп­ре­де­ле­ние век­то­ра по­ля­ри­за­ции.

3. Ка­кую ве­ли­чи­ну на­зы­ва­ют ди­элек­три­че­ской вос­при­им­чи­во­стью?

4. Дайте определение диэлектрической проницаемости среды.

5. Как связаны диэлектрическая проницаемость и диэлектрическая восприимчивость?

6. В чем заключается метод измерения диэлектрической проницаемости, используемый в работе?

7. Выведите формулу для вычисления e.

 

Используемая литература

[1] §§ 15.1, 15.2, 15.3;

[2] §§ 12.1-12.3;

[3] §§ 2.19, 5.66, 5.67, 5.68;

[4] т.2, §§ 15-19;

[5] §§ 87, 88.

Лабораторная работа 2-02

Изучение электрических свойств сегнетоэлектриков (ФПЭ-02)

Цель работы: изучение поляризации сегнетоэлектриков в зависимости от напряженности электрического поля Е, получение кривой , изучение диэлектрического гистерезиса, определение диэлектрических потерь в сегнетоэлектриках.

 

Теоретическое введение

Как известно, молекулы диэлектриков по своим электрическим свойствам эквивалентны электрическим диполям и могут обладать электрическим моментом.

(2.1)

где q – абсолютная величина суммарного заряда одного знака в молекуле (т.е. заряда всех ядер или всех электронов); - вектор, проведенный из “центра тяжести” отрицательных зарядов электронов в “центр тяжести” положительных зарядов ядер (плечо диполя).

Поляризация диэлектриков обычно описывается на основе представлений о жестких и индуцированных диполях. Внешнее электрическое поле либо упорядочивает ориентацию жестких диполей (ориентационная поляризация в диэлектриках с полярными молекулами), либо приводит к появлению полностью упорядоченных индуцированных диполей (поляризация электронного и ионного смещения в диэлектриках с полярными молекулами). Во всех этих случаях диэлектрики поляризуются.

Поляризация диэлектрика заключается в том, что под действием внешнего электрического поля суммарный электрический момент молекул диэлектрика становится отличным от нуля.

Количественной характеристикой поляризации диэлектрика служит вектор поляризованности (или вектор поляризации), который равен электрическому моменту единицы объема диэлектрика:

, (2.2)

где - векторная сумма дипольных электрических моментов всех молекул диэлектрика в малом объеме Δ V.

У изотропных диэлектриков поляризованность связана с напряженностью электрического поля в той же точке соотношением

(2.3)

где - коэффициент, не зависящий в первом приближении от Е и называемый диэлектрической восприимчивостью вещества; ε₀ = 8,85∙10^-12 Ф/м – электрическая постоянная.

Для описания электрического поля в диэлектриках, кроме напряженности и поляризованности , используют вектор электрического смещения , определяемый равенством:

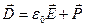(2.4)

С учетом (2.3) вектор смещения можно представить в виде:

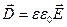, (2.5)

где – безразмерная величина, называемая диэлектрической проницаемостью среды. Для всех диэлектриков > 0, а ε > 1.

Сегнетоэлектрики представляют собой особую группу кристаллических диэлектриков, обладающих в отсутствие внешнего электрического поля в определенном интервале температур и давлений спонтанной (самопроизвольной) поляризацией, направление которой может быть изменено электрическим полем и в ряде случаев механическими напряжениями.

В отличие от обычных диэлектриков сегнетоэлектрики обладают рядом характерных свойств:

1. Сегнетоэлектрики характеризуются очень высокими значениями диэлектрической проницаемости . Она может достигать величин порядка 10³¸10⁶. Например, диэлектрическая проницаемость сегнетовой соли NaKC₄H₄O₆∙4H₂О при комнатной температуре (~20⁰ С) близка к 10000.

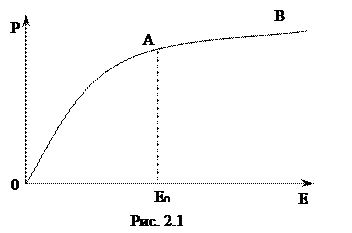2. Особенностью сегнетоэлектриков является нелинейный характер зависимости поляризованности Р, а значит, и электрического смещения D от напряженности поля Е (рис. 2.1). При этом диэлектрическая проницаемость сегнетоэлектриков ε оказывается зависящей от Е. На рис. 2.2 показана зависимость ε от Е для сегнетовой соли при температуре 20⁰ С.

3. Всем сегнетоэлектрикам свойственно явление диэлектрического гистерезиса, заключающееся в запаздывании изменения поляризованности Р (или смещения D) при изменении напряженности поля Е. Это запаздывание связано с тем, что величина Р (или D) не только определяется значением поля Е, но и зависит еще от предшествовавшего состояния поляризации образца. При циклических изменениях напряженности поля Е зависимость поляризованности Р и смещения D от Е выражается кривой, называемой петлей гистерезиса.

На рис. 2.3 представлена петля гистерезиса в координатах D, E.

С увеличением напряженности поля E смещение D в образце, который первоначально не был поляризован, изменяется по кривой ОАВ. Эта кривая называется начальной или основной кривой поляризации.

С уменьшением напряженности поля сегнетоэлектрик ведет себя сначала как обычный диэлектрик (на участке ВА гистерезис отсутствует), а затем (от точки А) изменение смещения отстает от изменения напряженности. Когда напряженность поля Е =0, сегнетоэлектрик остается поляризованным и величина электрического смещения, равная D _r, называется остаточным смещением.

Для снятия остаточного смещения к сегнетоэлектрику необходимо приложить электрическое поле противоположного направления с напряженностью – Е _с. Величину Е _с принято называть коэрцитивным полем.

Если максимальное значение напряженности поля таково, что спонтанная поляризация достигает насыщения, то получается петля гистерезиса, называемая петлей предельного цикла (сплошная кривая на рис. 2.3).

Если же при максимальной напряженности поля насыщение не достигается, то получается так называемая петля частного цикла, лежащая внутри предельного цикла (пунктирная кривая на рис. 2.3). Частных циклов переполяризации может существовать бесконечное множество, но при этом максимальные значения смещения D частных циклов всегда лежат на основной кривой поляризации OА.

4. Сегнетоэлектрические свойства сильно зависят от температуры. Для каждого сегнетоэлектрика существует такая температура Т _с, выше которой его сегнетоэлектрические свойства исчезают, и он превращается в обычный диэлектрик. Температура Т _с называется точкой Кюри. Для титаната бария BaTiO₃ точка Кюри равна 120⁰С. Некоторые сегнетоэлектрики имеют две точки Кюри (верхнюю и нижнюю) и ведут себя как сегнетоэлектрики лишь в температурном интервале между этими точками Кюри. К числу таковых относится сегнетова соль, для которой точки Кюри равны –18⁰С и +24⁰С.

На рис. 2.4 приведен график температурной зависимости диэлектрической проницаемости монокристалла BaTiO₃. Кристалл BaTiO₃ в сегнетоэлектрическом состоянии анизотропен. На рис. 2.4 левая ветвь графика относится к направлению в кристалле, перпендикулярному к оси спонтанной поляризации. В достаточно большом интервале температур значения ε BaTiO₃ существенно превышают значения ε обычных диэлектриков (для которых ε=1¸10). Вблизи точки Кюри наблюдается значительное возрастание ε (аномалия).

Все характерные свойства сегнетоэлектриков связаны с существованием у них спонтанной (самопроизвольной) поляризации. Спонтанная поляризация есть следствие собственной асимметрии элементарной ячейки кристалла, приводящей к появлению у нее дипольного электрического момента. В результате взаимодействия между отдельными поляризованными ячейками они располагаются так, что их электрические моменты ориентированы параллельно друг другу. Ориентация электрических моментов многих ячеек в одном направлении приводит к образованию областей спонтанной поляризации, называемых доменами. Очевидно, что каждый домен поляризован до насыщения. Линейные размеры доменов не превышают 10^{-6 м.}

В отсутствие внешнего электрического поля поляризованность всех доменов различна по направлению, поэтому в целом кристалл оказывается неполяризованным. Это показано на рис. 2.5, где схематически изображены домены образца, стрелками показаны направления спонтанной поляризации различных доменов. Под влиянием внешнего электрического поля в многодоменном кристалле происходит переориентация спонтанной поляризации. Этот процесс осуществляется:

а) смещением доменных стенок (домены, поляризованность которых составляет острый угол с внешним полем, растут за счет доменов, у которых ;

б) поворотом электрических моментов доменов в направлении поля;

в) образованием и прорастанием зародышей новых доменов, электрические моменты которых направлены по полю.

Перестройка доменной структуры, происходящая при наложении и увеличении внешнего электрического поля, приводит к появлению и росту суммарной поляризованности Р кристалла (нелинейный участок ОА на рис. 2.1 и 2.3). При этом вклад в суммарную поляризованность Р, помимо спонтанной поляризации, вносит также и индуцированная поляризация электронного и ионного смещения, т.е. Р = Р _s+ P _i.

При некоторой напряженности поля (в точке А, рис.2.1) во всем кристалле устанавливается единое направление спонтанной поляризации, совпадающее с направлением поля (рис. 2.5, б). Говорят, что кристалл становится однодоменным с направлением спонтанной поляризации, параллельным полю. Это состояние называется насыщением. Увеличение напряженности поля Е после достижения насыщения сопровождается дальнейшим ростом общей поляризованности Р кристалла, но теперь уже только за счет индуцированной поляризации (участок АВ на рис. 2.1 и 2.3). При этом поляризованность Р и смещение D практически линейно зависят от Е. Экстраполируя линейный участок АВ на ось ординат, можно оценить спонтанную поляризацию насыщения Р _s,max, которая приблизительно равна значению D _s, отсекаемому экстраполированным участком на оси ординат: P _{s max}≈ D _s. Это приблизительное равенство вытекает из того, что для большинства сегнетоэлектриков ε₀ Е << Р и D =ε₀ E + Р ≈ Р.

Как отмечалось выше, в точке Кюри при нагревании сегнетоэлектрика исчезают его особые свойства, и он превращается в обычный диэлектрик. Это объясняется тем, что при температуре Кюри происходит фазовый переход сегнетоэлектрика из полярной фазы, характеризуемой наличием спонтанной поляризации, в неполярную, в которой спонтанная поляризация отсутствует. При этом изменяется симметрия кристаллической решетки. Полярная фаза часто называется сегнетоэлектрической, а неполярная – параэлектрической.

Потери энергии в диэлектриках, находящихся в переменном электрическом поле, называемые диэлектрическими, могут быть связаны со следующими явлениями:

а) отставанием во времени поляризованности Р от напряженности поля Е из-за молекулярно-теплового движения;

б) наличием небольших токов проводимости;

в) явлением диэлектрического гистерезиса.

Во всех случаях происходит необратимое преобразование электрической энергии в теплоту.

Диэлектрические потери приводят к тому, что на участке цепи переменного тока, содержащем конденсатор, сдвиг по фазе между колебаниями тока и напряжения никогда не бывает точно равным , а всегда оказывается меньше, чем , на угол δ, называемый углом потерь. Диэлектрические потери в конденсаторах оцениваются тангенсом угла потерь:

, (2.6)

где Х – реактивное сопротивление конденсатора; R – сопротивление потерь в конденсаторе, определяемое из условия: мощность, выделяемая на этом сопротивлении при прохождении по нему переменного тока, равна мощности потерь в конденсаторе.

Тангенс угла потерь есть величина, обратная добротности Q:

,

и для его определения, наряду с (2.6), может быть использовано выражение

, (2.7)

где ∆ W – потери энергии за период колебаний (в элементе цепи или во всей цепи); W – энергия колебаний (максимальная для элемента цепи или полная для всей цепи).

Воспользуемся формулой (2.7) для оценки потерь энергии, вызванных диэлектрическим гистерезисом. Эти потери, как и сам гистерезис, есть следствие необратимого характера процессов, ответственных за переориентацию спонтанной поляризации.