| Прибыль, млн. руб. | Число органи-заций
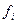
| Середина интервала, млн. руб.
|
|
| 
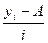
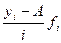
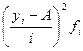
| Накопленная сумма частот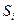 
|
| Итого | - | - | - |
4. Вычислить эмпирическое корреляционное отношение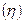 
:
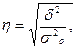
где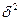 
– межгрупповая дисперсия прибыли; 
– общая дисперсия прибыли (см. расчетное значение 
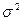, пункт 3).
Межгрупповая дисперсия прибыли вычисляется по формуле:
где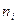 
– число организаций в группах по размеру уставного капитала; 
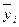– групповые средние значения прибыли; 
–общая средняя величина прибыли (см. расчетное значение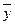 
, пункт 1).
Исходные данные для расчета межгрупповой дисперсии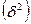 
содержатся в табл. 1.4 (графы 1, 2, 4). Расчетную часть оформить в табл. 2.3.:
Таблица 2.3
Расчет межгрупповой дисперсии прибыли
| Уставный капитал, млн. руб. | Число органи-заций
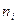
| Средняя прибыль
на одну организацию,
млн. руб.
| 
|
|
|
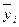
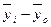
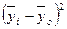
| Итого |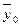 
| - | - |
Тесноту связи между уставным капиталом и прибылью можно оценить по шкале Чеддока:
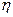
| 0.1 – 0.3 | 0.3 – 0.5 | 0.5 – 0.7 | 0.7 – 0.9 | 0.9 – 0.99 |
| Сила связи | Слабая | Умеренная | Заметная | Высокая | Весьма высокая |
Рекомендуемая литература
Гусаров В.М., Кузнецова Е.И. Статистика: учеб. пособие для студентов вузов, обучающихся по экономическим специальностям. – 2-е изд., перераб и доп. – М.: ЮНИТИ-ДАНА, 2007, – С. 61, 77-78.
Практикум по теории статистики: учеб. пособие / под ред. Р.А. Шмойловой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005, – С. 108-112, 124-128, 134-137.
Статистика: учебник / под ред. И.И. Елисеевой. – М.: КНОРУС, 2009, – С. 51-63, 67, 76-79.
Задание 3. АНАЛИЗ ФАКТОРНЫХ СВЯЗЕЙ МЕТОДОМ РЕГРЕССИИ И КОРРЕЛЯЦИИ
Проанализируйте взаимосвязь между стоимостью основных фондов и среднесуточной переработкой твердых коммунальных бытовых отходов по совокупности мусороперерабатывающих предприятий региона методами регрессии и корреляции. Сформулируйте выводы.
Исходные данные приведены в табл. 3.1.
Таблица 3.1
Распределение предприятий по стоимости основных фондов и объему переработки отходов
| № предприятия | Среднегодовая стоимость основных фондов, млн. руб. * | Среднесуточная переработка отходов, т * |
| 52.9 | ||
| 57.0 | ||
| 60.6 | ||
| 64.3 | ||
| 68.7 | ||
| 72.2 | ||
| 78.0 | ||
| 86.2 | ||
| 89.1 | ||
| 91.5 |
Методические рекомендации
1. С целью уточнения формы связи между признаками представить график зависимости среднесуточной переработки отходов от стоимости основных фондов. Точки, соответствующие стоимости основных фондов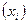 
и среднесуточной переработке отходов 
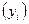, соединить отрезками прямой линии. Ломаную линию обозначить символом 
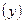. Используя графический метод, обосновать наличие прямолинейной зависимости между стоимостью основных фондов и объемом переработки отходов.
2. Записать уравнение регрессии, адекватное линейной зависимости:
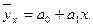
Рассчитать параметры уравнения регрессии, методом наименьших квадратов, используя систему нормальных уравнений:
где: 
– теоретические значения результативного признака;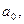 
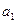– параметры уравнения регрессии; 
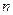– число единиц наблюдения (предприятий).
Приведенная система уравнений дает следующие формулы для нахождения параметров 
и 
:
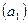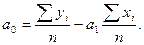
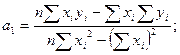
Представить конкретную регрессионную модель распределения предприятий по стоимости основных фондов и среднесуточной переработке отходов, подставив числовые значения параметров в исходное уравнение, как в следующем примере:
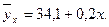
3. Рассчитать коэффициент эластичности 
:
Интерпретировать значения коэффициентов регрессии 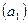и эластичности .
4. Определить теоретические значения прибыли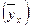 
по каждому предприятию, последовательно подставляя исходные данные о стоимости основных фондов 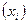в уравнение регрессии. Равенство сумм теоретических значений среднесуточной переработки отходов 
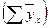и ее фактических значений 
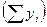свидетельствует о правильности расчетов.
Провести прямую линию через точки, соответствующие стоимости основных фондов 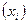и теоретическим значениям среднесуточной переработки отходов, обозначив ее символом .
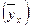5. Рассчитать коэффициент корреляции 
:
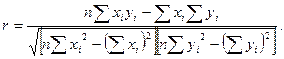
Сделать вывод о направлении и силе связи между стоимостью основных фондов и объемом переработки отходов. Для оценки тесноты связи использовать шкалу Чеддока.
6. Вычислить теоретическое корреляционное отношение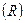 
на основе расчета факторной 
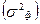и общей 
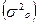дисперсии прибыли:
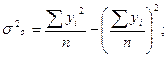
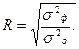
Совпадение значений коэффициента корреляции и теоретического корреляционного отношения 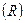подтверждает наличие линейной зависимости между признаками и правильность выполненных расчетов.
Расчетную часть задания оформить в табл. 3.2:
Рекомендуемая литература
Гусаров В.М., Кузнецова Е.И. Статистика: учеб. пособие для студентов вузов, обучающихся по экономическим специальностям. – 2-е изд., перераб и доп. – М.: ЮНИТИ-ДАНА, 2007, – С. 189-192, 195-197.
Практикум по теории статистики: учеб. пособие / под ред. Р.А. Шмойловой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005, – С. 191-195, 204-207.
Статистика: учебник / под ред. И.И. Елисеевой. – М.: КНОРУС, 2009, – С. 101-108.
Таблица 3.2
