| Уставный капитал, млн. руб. | Число организаций | Суммарная прибыль, млн. руб. | Средняя прибыль на одну организацию, млн. руб. (гр. 3: гр. 2) |
| 1 | 2 | 3 | 4 |
| 2 – 6 | 26.4 | 5.2 | |
| 6 - 10 | 69.9 | 11.7 | |
| … | … | … | … |
| Итого |
Для подсчета суммарной прибыли по каждой группе в графе 3 табл. 1.4 следует использовать данные графы 3 табл. 1.2. В итоговой строке итоговой графы табл. 1.4 приводится средний размер прибыли по совокупности организаций, полученный в результате деления итога графы 3 на итог графы 2.
Прослеживая изменение средней прибыли при переходе от одной группы к другой по мере возрастания уставного капитала, нужно сделать вывод о наличии и направлении связи (прямая, обратная) между исследуемыми признаками (уставным капиталом и прибылью).
4. Сгруппировать исследуемую совокупность организаций по величине прибыли. Для этого рекомендуется сформировать равные интервалы по использованной ранее методике, предварительно расположив значения прибыли в порядке их возрастания. Результаты группировки оформить в таблице 1.5., например:
Ранжированный ряд организаций
По величине прибыли, млн. руб.
3.1; 4.5; 4.7; 5.2; 5.6; 7.8; 8.2; …; 32.7.
Таблица 1.5
Группировка организаций по величине прибыли
| Прибыль, млн. руб. | Число организаций |
| 3 – 8 | |
| 8 – 13 | |
| 13 – 18 | |
| … | … |
| Итого |
5. Построить корреляционную таблицу в виде двухмерной группировки организаций по размеру уставного капитала и величине прибыли как в примере, приведенном в табл. 1.6.
На пересечении строк и граф обеих группировок, указать частоты, соответствующие численности организаций по двум признакам одновременно. При подсчете частот рекомендуется опираться на данные графы 3 табл. 1.2.
С помощью корреляционной таблицы визуально можно определить направление и силу связи между исследуемыми признаками. Расположение частот по диагонали из левого верхнего угла в нижний правый угол свидетельствует наличии прямой зависимости между признаками, распределение частот в противоположном направлении указывает на обратную связь. Беспорядочное размещение частот в таблице говорит об очень слабой связи или ее отсутствии. Учитывая направление расположения частот, сделать вывод о направлении и силе связи между уставным капиталом и прибылью.
Таблица 1.6
Группировка организаций по размеру уставного капитала и
Величине прибыли
 Прибыль,
млн. руб.
Уставный
капитал, млн. руб.
| 3 – 8 | 8 – 13 | 13 – 18 | … | Итого |
| 2 – 6 | - | - | … | ||
| 6 – 10 | … | ||||
| 10 – 14 | - | … | |||
| 14 – 18 | - | … | |||
| 18 – 22 | - | - | … | ||
| 22 – 26 | - | - | - | … | |
| Итого | … |
Рекомендуемая литература
Гусаров В.М., Кузнецова Е.И. Статистика: учеб. пособие для студентов вузов, обучающихся по экономическим специальностям. – 2-е изд., перераб и доп. – М.: ЮНИТИ-ДАНА, 2007, – С. 37-38.
Практикум по теории статистики: учеб. пособие / под ред. Р.А. Шмойловой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2005, – С. 35-42.
Статистика: учебник / под ред. И.И. Елисеевой. – М.: КНОРУС, 2009, – С. 29-30.
Задание 2. РАСЧЕТ СРЕДНИХ ВЕЛИЧИН И ВАРИАЦИОННЫЙ АНАЛИЗ
Вычислите среднюю арифметическую величину, моду, медиану, дисперсию, среднее квадратическое отклонение и коэффициент вариации прибыли организаций по сгруппированным данным. Рассчитайте эмпирическое корреляционное отношение и оцените тесноту связи между уставным капиталом и прибылью. Сформулируйте выводы.
В качестве исходного материала используйте данные табл. 1.5.
Методические рекомендации
1. Рассчитать среднюю арифметическую величину прибыли 
способом моментов:
где 
– середина (среднее значение) каждого интервала;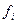 
– частота (число организаций в каждой группе); 
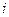– величина интервала; 
– середина интервала с наибольшей частотой.
Объяснить целесообразность использования в расчетах способа моментов.
2. Вычислить моду и медиану. Охарактеризовать результаты вычислений.
Мода находится в интервале с наибольшей частотой и определяется по формуле
где 
– мода; 
– нижняя граница модального интервала;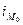 
– величина модального интервала; 
– частота модального интервала; 
– частота интервала, предшествующего модальному; 
– частота интервала, следующего за модальным.
В медианном интервале накопленная сумма частот должна быть не менее половины суммы частот:
Медиана исчисляется по формуле
где 
– медиана;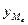 
– нижняя граница медианного интервала; 
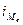– величина медианного интервала; 
– накопленная сумма частот в интервале, расположенном перед медианным; 
– частота медианного интервала.
3. Определить дисперсию, среднее квадратическое отклонение и коэффициент вариации прибыли по формулам, представленным в табл. 2.1:
Таблица 2.1
Показатели вариации
| Наименование показателей | Расчетная формула |
1. Дисперсия
| 
|
2. Среднее квадратическое
отклонение 
| 
|
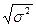
3. Коэффициент вариации 
| 
|
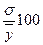
Оценить однородность совокупности организаций по величине прибыли. Есликоэффициент вариации не превышает 33%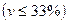 
, совокупность считается однородной, а средняя величина является надежной ее характеристикой.
Расчетную часть задания оформить в табл. 2.2.
Таблица 2.2
