(для каждого коэффициента регрессии вычислить коэффициент эластичности, β-коэффициент)
Учитывая, что коэффициент регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, расчитаем коэффициенты эластичности (Э) и бета-коэффициенты, по следующим формулам:
 ;
;
Используя математические и статистические функции, найдем средние значения переменных и средние квадратические отклонения.

Рассчитаем коэффициенты эластичности. Коэффициент эластичности показывает, на сколько процентов в среднем изменится зависимая переменная, если фактор изменится на 1%

Таким образом, при увеличении только расходов домохозяйств на 1% индекс человеческого развития уменьшится в среднем на 0,053%, а при увеличении только ожидаемой продолжительности жизни при рождении 1997 года на 1% индекс человеческого развития увеличится в среднем на 1,682%.
Рассчитаем бета-коэффициенты.Бета-коэффициент с математической точки зрения показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднеквадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных.

Таким образом, бета-коэффициенты показывают, что, так как коэфффициент β2>β1, то второй фактор оказывает на индекс человеческого развития большее влияние, чем первый.
Варианты индивидуальных заданий.
Задача 1.
По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн.руб.) от объема капиталовложений (X, млн.руб.)
Требуется:
1) Построить поле корреляции и сформулировать гипотезу о форме связи.
2) Найти параметры уравнения линейной регрессии и дать ему экономическую интерпретацию.
3) Оценить тесноту связи с помощью показателей корреляции и детерминации.
4) Проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05) и с помощью средней относительной ошибки аппроксимации. Сделать вывод о качестве модели.
5) Проверить выполнимость предпосылок МНК.
6) Рассчитать параметры уравнений степенной и гиперболической регрессий. Дать интерпретацию уравнению степенной регрессии
7) Рассчитать индексы корреляции и детерминации.
8) Оценить значимость построенных моделей регрессий с помощью F-критерия Фишера и средней относительной ошибки аппроксимации. Сделать выводы.
9) С помощью сравнения основных характеристик выбрать лучшее уравнение регрессии и сделать вывод.
10) Осуществите прогнозирование среднего показателя Y при уровне значимости α=0,05, если прогнозное значение фактора Х составит 80% от его максимального значения. Определите доверительный интервал прогноза.
Вариант 1.
| x | ||||||||||
| y |
Вариант 2.
| x | ||||||||||
| y |
Вариант 3.
| x | ||||||||||
| y |
Вариант 4.
| x | ||||||||||
| y |
Вариант 5.
| x | ||||||||||
| y |
Вариант 6.
| x | ||||||||||
| y |
Вариант 7.
| x | ||||||||||
| y |
Вариант 8.
| x | ||||||||||
| y |
Вариант 9.
| x | ||||||||||
| y |
Вариант 10.
| x | ||||||||||
| y |
Задача 2.
Вариант 1:  Вариант 5:
Вариант 5:  Вариант 9:
Вариант 9: 
Вариант 2:  Вариант 6:
Вариант 6: 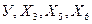 Вариант 10:
Вариант 10: 
Вариант 3: 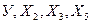 Вариант 7:
Вариант 7: 
Вариант 4:  Вариант 8:
Вариант 8: 
По данным, представленным в таблице, изучается зависимость индекса человеческого развития y от переменных:
х1 – ВВП на душу населения, тыс. $, по итогам 2009г;
х2 – фактическое конечное потребление домашних хозяйств по паритету покупательной способности на душу населения (Россия = 100);
х3 –индекс потребительских цен в %;
х4 – ожидаемая продолжительность жизни при рождении 2009г., число лет;
х5 - суточная колорийность питания населения, ккал на душу населения;
х6 – расходы на здравоохранение, % к ВВП.
| Страны | y | x1 | x2 | x3 | x4 | x5 | x6 |
| Австралия | 0,97 | 39,9 | 8,5 | ||||
| Австрия | 0,955 | 39,2 | |||||
| Белоруссия | 0,826 | 12,5 | 5,8 | ||||
| Бельгия | 0,953 | 36,8 | 11,8 | ||||
| Великобритания | 0,947 | 34,2 | 9,3 | ||||
| Германия | 0,947 | 34,2 | 8,1 | ||||
| Дания | 0,955 | 35,9 | |||||
| Индия | 0,612 | 3,2 | 4,1 | ||||
| Испания | 0,955 | 29,3 | 9,7 | ||||
| Италия | 0,951 | 29,9 | 9,7 | ||||
| Канада | 0,966 | 38,1 | 10,9 | ||||
| Казахстан | 0,804 | 11,8 | 4,3 | ||||
| Китай | 0,772 | 6,7 | 5,1 | ||||
| Латвия | 0,866 | 14,5 | 8,1 | ||||
| Нидерланды | 0,964 | 39,4 | 10,8 | ||||
| Норвегия | 0,971 | 57,6 | 9,7 | ||||
| Польша | 0,88 | 17,9 | 7,1 | ||||
| Россия | 0,817 | 15,1 | 5,1 | ||||
| США | 0,956 | 16,2 | |||||
| Украина | 0,796 | 6,3 | |||||
| Финляндия | 0,959 | 34,1 | 11,7 | ||||
| Франция | 0,961 | 32,5 | |||||
| Чехия | 0,903 | 24,8 | 7,6 | ||||
| Швейцария | 0,96 | 41,2 | 11,3 | ||||
| Швеция | 0,963 | 9,9 |
Требуется:
1. Осуществить выбор факторных признаков для построения двухфакторной регрессионной модели.
2. Рассчитать параметры модели.
3. Для оценки качества всего уравнения регрессии определить:
- линейный коэффициент множественной корреляции;
- коэффициент детерминации.
4. Осуществить оценку значимости уравнения регрессии.
5. Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии.
6. Оценить влияние факторов на зависимую переменную по модели. Для этого рассчитайте:
- β-коэффициенты;
- коэффициенты эластичности.
Тестовые задания по теме «Корреляционно-регрессионный анализ»
Задание 1. Дополните определение:
1.1. Односторонняя статистическая связь между переменными называется _____________________.
1.2. Регрессией называется ___________________________________________________________.
Задание 2. Простая линейная регрессия задается уравнением ________________________________.
Задание 3. Уравнение показательной функции имеет вид ___________________________________
Задание 4. Уравнение вида  задает _____________________________________________
задает _____________________________________________
Задание 5. Зависимость между переменными называется корреляционной, если:
а) каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного признака,
б) каждому значению факторного признака соответствует множество значений результативного признака, т.е. определенное статистическое распределение,
в) каждому значению факторного признака соответствует целое распределение значений результативного признака,
г) каждому значению факторного признака соответствует строго определенное значение факторного признака.
Задание 6. Параметр в0 в уравнении парной линейной регрессии:
а) показывает среднее изменение результата при изменении фактора на 1 единицу,
б) не имеет экономического смысла,
в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.
г) показывает среднее изменение фактора при изменении результата на 1 единицу.
Задание 7. Параметр в1 в уравнении парной линейной регрессии:
а) показывает среднее изменение результата при изменении фактора на 1 единицу,
б) оценивает статистическую значимость уравнения регрессии,
в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.
г) показывает среднее изменение фактора при изменении результата на 1 единицу.
Задание 8. Параметр в1 в степенной модели является коэффициентом:
а) регрессии, б) эластичности, в) детерминации, г) корреляции.
Задание 9. Среднее изменение результата при изменении фактора на 1 единицу в уравнении парной линейной регрессии  показывает:
показывает:
а) параметр в0, б) переменная  , в) переменная х, г) параметр в1.
, в) переменная х, г) параметр в1.
Задание 10. Установите, какой из коэффициентов определяет среднее изменение результативного признака при изменении факторного признака на 1%:
а) коэффициент регрессии, в) коэффициент детерминации,
б) коэффициент эластичности, г) коэффициент корреляции.
Задание 11. Средняя ошибка аппроксимации  показывает:
показывает:
а) На сколько процентов в среднем расчетные значения у для модели отличаются от фактических значений
б) На сколько процентов увеличивается точность оценок
в) На сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1% от своего среднего значения.
Задание 12. Определите, какие из уравнений задают простую линейную регрессию У на Х:
а)  , б)
, б)  , в)
, в)  , г)
, г) 
Задание 13. Уравнение степенной функции имеет вид:
а)  б)
б)  в)
в)  г)
г) 
Задание 14. Формула для расчета коэффициента эластичности имеет вид:
а)  б)
б)  в)
в)  г)
г) 
Задание 15. Функция вида  является:
является:
а) полиномом, б) степенной, в) показательной, г) гиперболой.
Задание 16. Определите, какие из указанных моделей нельзя свести к линейному виду:
а)  б)
б) 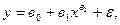 в)
в) 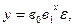 г)
г) 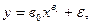
Задание 17. Верно ли, что полином второй степени является регрессией, нелинейной по переменным, но линейной по оцениваемым параметрам:
а) да, б) нет.
Задание 18. Индекс корреляции определяется по формуле:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
Задание 19. Формула для расчета коэффициента нелинейной корреляции имеет вид:
а)  б)
б)  в)
в)  г)
г) 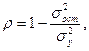
Задание 20. Верно ли, что индекс нелинейной корреляции принимает значения от -1 до 1:
а) да, б) нет.
Задание 21. Определите, какое из значений не может принимать парный коэффициент корреляции:
а) -0,973; б) 0,005; в) 1,111; г) 0,721.
Задание 22. Коэффициент b1 регрессии:
а) всегда находится в пределах от -1 до 1; б) никогда не бывает отрицательным;
в) равен коэффициенту корреляции; г) не может быть равен нулю;
д) может принимать любые значения.
Задание 23. Если парный линейный коэффициент корреляции характеризует наличие слабой связи, значит он принимает следующее значение:
а) 1,2; б)-0,82; в) 0,23; г) 0,92; д)-0,24.
Задание 24. Зависимость спроса от цен описали уравнением регрессии  . Уравнение показывает, что:
. Уравнение показывает, что:
а) с увеличением цен на 1% спрос снижается на 2,7%.
б) с уменьшением цен на 1% спрос увеличивается на 2,7%.
в) с увеличением цен на 1% спрос увеличивается на 2,7%.
г) с увеличением цен на 2,7% спрос уменьшается на 1%.
Задание 25. Коэффициент регрессии в линейной регрессии совокупного спроса на мобильные телефоны (в тысячах рублей) по цене (в рублях) оказался равным -1. Это означает:
а) увеличение цены на 1% снижает спрос на мобильные телефоны на 1%;
б) увеличение цена на 1 рубль снижает спрос на мобильные телефоны на 1%;
в) увеличение цены на 1% снижает спрос на мобильные телефоны на 1 тысячу рублей;
г) увеличение цены на 1 рубль снижает спрос на мобильные телефоны на 1 тысячу рублей;
д) полученное число никак не интерпретируется.
Задание 26. Линейный коэффициент корреляции меньше нуля, это означает, что
а) связь между переменными тесная; б) связь между переменными прямая;
в) связь между переменными обратная; г) связь между переменными отсутствует;
д) нет правильного ответа.
Задание 27. Для характеристики зависимости расходов на питание от личного располагаемого дохода рассчитали регрессию 
 . Эластичность спроса по доходу составляет:
. Эластичность спроса по доходу составляет:
а) 3,34% б) 0,45% в) 3,79% г)14,36
Задание 28. Оценка параметров в уравнении простой линейной регрессии может быть найдена с помощью:
а) метода частных средних. в) диаграммы рассеяния,
б) метода наименьших модулей г) метода наименьших квадратов,
д) метода математической индукции.
Задание 29. Суть метода наименьших квадратов заключается в:
а) минимизации суммы квадратов коэффициентов регрессии,
б) минимизации квадратов отклонений значений зависимой переменной,
в) минимизации суммы остаточных членов,
г) минимизации квадратов отклонений эмпирических значений зависимой переменной от значений, найденных по уравнению регрессии.
Задание 30. Согласно методу наименьших квадратов минимизируется выражение:
а)  , б)
, б)  , в)
, в)  , г)
, г) 
Задание 31. Среди предложенных выберите истинные утверждения:
а) Метод наименьших квадратов позволяет оценить параметры в уравнении простой линейной регрессии.
б) В регрессионной модели зависимая переменная является фактором изменения объясняющей переменной.
в) Метод частных средних применяется для отыскания параметров в уравнении простой линейной регрессии.
г) В регрессионной модели объясняющая переменная является фактором изменения зависимой переменной.
Задание 32. Среди предложенных выберите ложные утверждения:
а) В регрессионной модели зависимая переменная является фактором изменения объясняющей переменной.
б) Метод частных средних применяется для предварительного анализа зависимости между переменными.
в) В регрессионной модели объясняющая переменная является фактором изменения зависимой переменной.
г) Метод наименьших квадратов позволяет оценить параметры в уравнении простой линейной регрессии.
Задание 33. Установите соответствие между утверждениями 1)- 4) из первого столбца таблицы и утверждениями а)-е) из второго столбца таблицы. Ответ запишите в третий столбец таблицы.
1) Модель вида  ( ( ) )
| а) определяет коэффициент эластичности 1,78 | 1) - |
2) Модель вида  ( ( ) )
| б) задает нелинейную регрессию у на х | 2) - |
3) Модель вида  ( ( ) )
| в) определяет множественную регрессию | 3) - |
4) Модель вида  ( (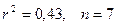 ) )
| г) задает линейную регрессию у на х | 4) - |
| д) является значимым на уровне 0,05 | ||
| е) характеризуется достаточно сильной связью между переменными |
Задание 34. Установите соответствие между названием модели и видом ее уравнения:
1.гипербола
2.парабола третьего порядка
3многофакторная
4. линейная
Варианты ответа:
| A) | 
| B) | 
| |
| C) | 
| D) | 
|
Задание 35. Графическая модель гиперболы имеет вид:

Задание 36. Мультиколлинеарность нежелательна при проведении регрессионного анализа
потому, что:
а) вызывает автокорреляцию в остатках; б) искажает смысл коэффициентов регрессии;
в) нарушает предпосылки МНК; г) нарушает гомоскедастичность остатков.
Задание 37. Табличное значение F-критерия Фишера меньше расчетного F-критерия Фишера. Это значит:
а) уравнение регрессии значимо,
б) все коэффициенты уравнения регрессии равны нулю;
в) не все коэффициенты уравнения регрессии равны нулю,
г) уравнение регрессии незначимо.
Задание 38. Имеются следующие данные: коэффициент регрессии  , стандартная ошибка коэффициента регрессии
, стандартная ошибка коэффициента регрессии  . Определите t-критерий Стьюдента и оцените значимость коэффициента регрессии
. Определите t-критерий Стьюдента и оцените значимость коэффициента регрессии  , если
, если 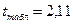 при уровне значимости
при уровне значимости  .
.
а) 0,207, коэффициент незначим; б) 4,841, коэффициент значим;
в) 4,841 коэффициент незначим; г) 0,207, коэффициент значим.
Задание 39. Если парный коэффициент корреляции между признаками Y и X принимает значение 0,675, то коэффициент детерминации равен:
а) 0,822; б) - 0,675; в) 0,576; г) 0,456.
Задание 40. Результаты исследования по 16 городам региона показали, что теснота связи между среднедушевым денежным доходом и среднедушевым оборотом розничной торговли равна 0, 706. Фактическое значение F- критерия Фишера для проверки значимости уравнения парной линейной регрессии в целом равно:
а) 0,498; б) 33,619; в) 13,888; г) 15,873.
Задание 41. По совокупности 25 предприятий торговли изучается зависимость между признаками: х – цена на товар А, тыс. руб.; у - прибыль торгового предприятия, млн. руб. При оценке регрессионной модели были получены следующие промежуточные результаты:  и
и 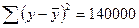 . Показатели корреляции равен _______________________. Показатель детерминации равен ____________________________.
. Показатели корреляции равен _______________________. Показатель детерминации равен ____________________________.
Задание 42. Изучалась зависимость вида  . Получены следующие данные:
. Получены следующие данные:  ;
;  . Коэффициент парной линейной корреляции, если объем совокупности n=7, равен ______________________________________________________
. Коэффициент парной линейной корреляции, если объем совокупности n=7, равен ______________________________________________________
Задание 43. Уравнение регрессии имеет вид 
 Тогда коэффициент эластичности равен:
Тогда коэффициент эластичности равен:
а) 0,94, б) 1,68, в) 0,65, г) 2,42
Задание 44. Множественная линейная регрессия задается уравнением:
а)  , б)
, б)  ,
,
в)  г)
г) 
Задание 45. Частные коэффициенты корреляции:
а) характеризуют тесноту связи рассматриваемого набора факторов с исследуемым признаком;
б) содержат поправку на число степеней свободы и не допускают преувеличения тесноты связи;
в) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.
Задание 46. Определите, в каких пределах изменяется множественный коэффициент корреляции:
а)  ; б)
; б)  ; в)
; в)  г) другой ответ _________________
г) другой ответ _________________
Задание 47. Множественный коэффициент корреляции  Определите, какой процент дисперсии зависимой переменной у объясняется влиянием факторов х1 и х2:
Определите, какой процент дисперсии зависимой переменной у объясняется влиянием факторов х1 и х2:
а) 75%; 6) 81%; в) 25%; г) 56%.
Задание 48. Уравнение множественной регрессии имеет вид:  . Параметр
. Параметр  означает, что:
означает, что:
а) при увеличении  на одну единицу своего измерения переменная y увеличится на 1,37 единиц своего измерения;
на одну единицу своего измерения переменная y увеличится на 1,37 единиц своего измерения;
б) при увеличении  на одну единицу своего измерения и при фиксированном значении фактора
на одну единицу своего измерения и при фиксированном значении фактора  , переменная y увеличится на 1,37 единиц своего измерения;
, переменная y увеличится на 1,37 единиц своего измерения;
в) при увеличении  на 1,37 единиц своего измерения и при фиксированном значении фактора
на 1,37 единиц своего измерения и при фиксированном значении фактора  , переменная y увеличится на одну единицу своего измерения.
, переменная y увеличится на одну единицу своего измерения.
Задание 49. Уравнение множественной регрессии имеет вид:  . Параметр
. Параметр  означает, что:
означает, что:
а) при увеличении  на одну единицу своего измерения переменная y увеличится на 0,367 единиц своего измерения;
на одну единицу своего измерения переменная y увеличится на 0,367 единиц своего измерения;
б) при увеличении  на одну единицу своего измерения и при фиксированном значении фактора
на одну единицу своего измерения и при фиксированном значении фактора  , переменная y увеличится на 0,367 единиц своего измерения;
, переменная y увеличится на 0,367 единиц своего измерения;
в) при увеличении  на 0,367 единиц своего измерения и при фиксированном значении фактора
на 0,367 единиц своего измерения и при фиксированном значении фактора  , переменная y увеличится на одну единицу своего измерения.
, переменная y увеличится на одну единицу своего измерения.
г) при увеличении  на одну единицу своего измерения и при фиксированном значении фактора
на одну единицу своего измерения и при фиксированном значении фактора  , переменная y увеличится в 0,367 раз.
, переменная y увеличится в 0,367 раз.
Задание 50. По 25 предприятиям отрасли было получено следующее уравнение регрессии  зависимости объема выпуска продукции у (млн.руб.) от численности занятых на предприятии
зависимости объема выпуска продукции у (млн.руб.) от численности занятых на предприятии  (чел.) и среднегодовой стоимости основных фондов
(чел.) и среднегодовой стоимости основных фондов  (млн.руб.). Дайте интерпретацию полученному уравнению _____________________________________________________.
(млн.руб.). Дайте интерпретацию полученному уравнению _____________________________________________________.
Задание 51. Коэффициент множественной детерминации показывает:
а) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на1%;
б) долю вариации зависимой переменной, обусловленную вариацией независимых переменных;
в) на какую часть своего стандартного отклонения изменится зависимая переменная, если независимая переменная изменится на величину своего стандартного отклонения;
г) насколько изменится зависимая переменная, если независимая переменная изменится на единицу;
д) нет правильного ответа.
Тестовые задания по теме «Временные ряды»
Задание 1. Дополните определение:
Ошибки первого рода – это ______________
Задание 2. Среди предложенных вариантов выберите виды временных рядов:
а) случайные, б) моментные, в) периодические, г) сезонные, д) интервальные.
Задание 3. Метод простой скользящей средней относится к числу методов:
а) определения существования тренда во временном ряду,
б) сглаживания временных рядов,
в) определения аномальных значений уровней временного ряда,
г) выявления составляющих временного ряда.
Задание 4. Среди предложенных утверждений выберите истинные:
а) Недостатком прогнозирования с использованием среднего прироста и среднего темпа роста является то, что они учитывают только промежуточные уровни, исключая влияние начального и конечного уровней временного ряда.
б) Для выявления аномальных уровней временного ряда используется метод «восходящих» и «нисходящих» серий.
в) Если расчетное значение  для уровня t меньше табличного значения, то соответствующее значение уровня
для уровня t меньше табличного значения, то соответствующее значение уровня  ряда считается аномальным.
ряда считается аномальным.
г) Ряд, полученный из средних или относительных величин какого-либо показателя, является производным рядом.
Задание 5. Определите вид данного временного ряда
| квартал, t | 1-й кв. 2002 г | 2-й кв. 2002 г | 3-й кв. 2002 г | 4-й кв. 2002 г | 1-й кв. 2003 г | 2-й кв. 2003 г |
| yt | 21,19 | 22,24 | 23,27 | 24,32 | 25,35 | 26,38 |
а) периодический, б) моментный, в) случайный, г) интервальный.
Задание 6. Дополните определение:
Построение аналитической функции для моделирования тенденции временного ряда называется …
Задание 7. Среди предложенных вариантов выберите компоненты временных рядов:
а) циклическая компонента, б) бренд, в) периодическая компонента,
г) сезонная компонента, д) детерминированная компонента, е) случайная компонента.
Задание 8. Для определения аномальных значений уровней временного ряда используется:
а) метод взвешенной скользящей средней,
б) критерий Ирвина,
в) критерий «восходящих» и «нисходящих» серий,
г) метод наименьших квадратов.
Задание 9. Среди предложенных утверждений выберите ложные:
а) Для выравнивания рядов с нелинейной тенденцией развития используется метод простой скользящей средней.
б) Временные ряды бывают моментные, периодические и случайные.
в) Сезонная компонента отражает повторяемость экономических процессов в течение не очень длительного времени.
г) Если временной ряд представлен в виде суммы составляющих компонент, то модель ряда называется аддитивной.
Задание 10. Дополните определение:
Под прогнозом понимается _____________
Задание 11. Критерий Дарбина-Уотсона применяется для:
а) определения наличия сезонных колебаний, б) оценки значимости построенной модели,
в) определения автокорреляции в остатках, г) устранения тенденции во временном ряде.
Задание 12. К первому классу кривых роста относятся:
а) полиномы второй степени, б) кривая Гомперца, в) показательная кривая, г) линейная функция.
Задание 13. Абсолютная ошибка прогноза определяется по формуле:
а)  , б)
, б) 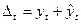 в)
в)  , г)
, г)  .
.
Задание 14. Для прогнозирования временного ряда длиной 17 выбрана линейная модель. Значение d-критерия равно 1,41. Тогда с доверительной вероятностью 0,95:
а) нет достаточных оснований для принятия решения об адекватности модели реальному процессу,
б) модель адекватна реальному процессу,
в) модель неадекватна реальному процессу.
Задание 15. Имеются данные об урожайности озимой пшеницы yt за 10 лет:
| t | ||||||||||
| yt | 16,2 | 20,1 | 17,2 | 7,8 | 15,2 | 16,2 | 19,7 | 14,5 | 18,6 | 20,4 |
Проверьте на аномальность уровень t = 4. σу =3,76. Сделайте вывод.
Задание 16. Динамика потребления овощей на одного члена домохозяйства в области за 1993-2001 гг. характеризуется следующими данными:
| Годы | |||||||||
| Потребление овощей, кг. | 30,0 | 32,1 | 36,0 | 30,9 | 38,7 | 48,9 | 46,8 | 53,4 | 54,0 |
Произведите сглаживание временного ряда уt методом скользящих средних, используя простую среднюю арифметическую с интервалом сглаживания m = 3.
16.1. Выберите нужную формулу
a)  б)
б)  в)
в) 
16.2. Запишите полученные результаты___________________________________
Задание 17.
В таблице представлены квартальные данные об объеме производства в денежном выражении (ден.ед.)
| Квартал | 1-й квартал 2006 | 2-й квартал 2006 | 3-й квартал 2006 | 4-й квартал 2006 | 1-й квартал 2007 | 2-й квартал 2007 |
| Уt | 21,18 | 22,23 | 23,26 | 24,31 | 25,34 | 26,37 |
Определите прогноз производства в 3-м квартале 2007 года с помощью среднего прироста.
Вопросы к экзамену по курсу «Эконометрика»
- Причинная связь. Основные типы причинных связей.
- Функциональные и стохастические зависимости.
- Понятие регрессии. Регрессия как односторонняя стохастическая зависимость. Различные виды регрессии: простая, множественная, линейная, нелинейная, положительная, отрицательная, непосредственная, косвенная, нонсенс-регрессия.
4. Приемы предварительного анализа зависимости между двумя переменными.
5. Простая линейная регрессия.
6. Построение регрессионной прямой с помощью метода наименьших квадратов (по несгруппированным данным).
7. Сопряженные регрессионные прямые.
8. Линейная множественная регрессия.
9. Нелинейная регрессия. Квазилинейные функции.
10. Нелинейная регрессия. Нелинейные функции второго класса.
11. Понятие корреляции. Различные виды корреляции: положительная или прямая, отрицательная или обратная, множественная, частная, линейная, нелинейная, непосредственная, косвенная, нонсенс-корреляция.
12. Линейная корреляция. Простая линейная корреляция при несгруппированных данных.
13. Линейная множественная корреляция. Частная корреляция. Соотношение между коэффициентами множественной и частной корреляции, регрессии и детерминации.
14. Корреляция для нелинейной регрессии.
15. Оценка качества построенной модели. F – критерий Фишера. Средняя ошибка аппроксимации.
- Определение интервалов прогноза по линейному уравнению регрессии.
17. Эконометрическое моделирование. Типы эконометрических моделей.
18. Этапы эконометрического моделирования.
19. Предмет эконометрики. Задачи, решаемые с помощью эконометрики.
20. Понятие и классификация временных рядов.
21. Аномальные значения уровней временного ряда. Метод Ирвина.
22. Общие составляющие (компоненты) уровней временного ряда.
23. Проверка гипотезы существования тенденции (тренда).
24. Автокорреляция уровней временного ряда и выявление его структуры.
25. Моделирование тенденции временного ряда.






