Парная регресия и корреляция
Изучается зависимость стоимости квартиры (Y, тыс.$) от ее полезной площади (Х, м2)
| x | ||||||||||
| Y |
Требуется:
1) Построить поле корреляции и сформулировать гипотезу о форме связи.
2) Найти параметры уравнения линейной регрессии МНК и дать ему экономическую интерпретацию.
3) Оценить тесноту связи с помощью показателей корреляции и детерминации.
4) Проверить значимость уравнения регрессии с помощью F-критерия Фишера (α=0,05) и с помощью средней относительной ошибки аппроксимации. Сделать вывод о качестве модели.
5) Проверить выполнимость предпосылок МНК.
6) Рассчитать параметры уравнения степенной и гиперболической регрессии. Дать интерпретацию уравнению степенной регрессии
7) Рассчитать индексы корреляции и детерминации.
8) Оценить значимость построенных регрессий с помощью F-критерия Фишера и средней относительной ошибки аппроксимации. Сделать выводы.
9) С помощью сравнения основных характеристик выбрать лучшее уравнение регрессии и сделать вывод.
10) Осуществить прогнозирование среднего показателя Y при уровне значимости α=0,05, если прогнозное значение фактора Х составит 80% от его максимального значения. Определить доверительный интервал прогноза.
Решение.
1) Построим поле корреляции.
По виду поля корреляции можно предположить наличие линейной корреляционной зависимости Y по х между двумя рассматриваемыми переменными. Но возможно и построение степенной модели, показательной или гиперболической регрессий.
2) Построим линейную модель парной регрессии 
.
Рабочая таблица. (При составлении этой таблицы можно воспользоваться математическими функциями ППП Excel)
| N | х | Y | x2 | Xy | y2 |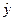 
| 
| 
| 
|
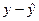
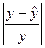
| 35,03 | 2,97 | 8,82 | 0,08 | ||||||
| 29,27 | -3,27 | 10,70 | 0,12 | ||||||
| 40,07 | -0,07 | 0,0049 | 0,0017 | ||||||
| 46,55 | -1,55 | 2,40 | 0,03 | ||||||
| 45,83 | 5,17 | 26,73 | 0,10 | ||||||
| 47,99 | 1,01 | 1,02 | 0,02 | ||||||
| 27,11 | 6,89 | 47,47 | 0,20 | ||||||
| 35,75 | -0,75 | 0,56 | 0,02 | ||||||
| 45,83 | -3,83 | 14,67 | 0,09 | ||||||
| 29,99 | -5,99 | 35,88 | 0,25 | ||||||
| Сумма | 0,58 | 148,25 | 0,91 |
Значения параметров а и b линейной модели определим, используя данные таблицы
Уравнение линейной регрессии имеет вид:
С увеличением полезной площади квартиры на 1м2 стоимость увеличивается в среднем на 0,72 тыс.$.
3) Рассчитаем линейный коэффициент парной корреляции по следующей формуле:
 |
Можно сказать, что связь между полезной площадью квартиры Х и ее стоимостью У прямая, достаточно сильная.
Рассчитаем коэффициент детерминации: Ryx=r2yx=0,794
Вариация результата У (стоимость квартиры) на 79,4% объясняется вариацией фактора Х (полезной площадью). На остальные факторы, неучтенные в модели, приходится 20,6%.
4) Оценку значимости уравнения регрессии проведем с помощью F-критерий Фишера:
для α=0,05; k1=m=1, k2=n-m-1=8, где m-число объясняющих факторов в модели.
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, так как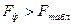 
Определим среднюю относительную ошибку аппроксимации:
В среднем расчетные значения 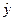для линейной модели отличаются от фактических значений на 9,1%, что находится в пределах нормы, то есть качество модели хорошее.
Проверим предпосылки МНК.
а) Проверка равенства математического ожидания остаточной последовательности нулю.
Вычислим среднее значение ряда остатков.
.
Так как 
, то модель не содержит постоянной систематической ошибки и адекватна по критерию нулевого среднего.
б) Проверка свойства гомоскедастичности
Расположим значения факторного признака 
в порядке возрастания.
Разделим совокупность наблюдений на две группы и для каждой группы с помощью программы Анализ данных в EXCEL, инструмент Регрессия определим параметры уравнений регрессий и остаточные суммы квадратов.
Таблица 2.4
Расчётные значения
| Уравнение регрессии | Остаток | |
| 1 группа | 
| 
|
| 2 группа | 
| 
|
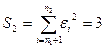
Расчетный критерий равен: 
.
Табличное значение F -критерия с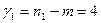 
и 
степенями свободы и при доверительной вероятности 0,95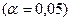 
равно 6,39.
Величина 
не превышает табличное значение F -критерия, следовательно, свойство гомоскедастичности выполняется.
в) Проверку независимости последовательности остатков (отсутствие автокорреляции) осуществим с помощью d -критерия Дарбина-Уотсона.
.
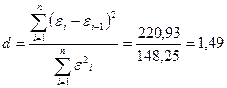Расчетное значение критерия сравнивается с нижним 
и верхним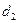 
критическими значениями статистики Дарбина-Уотсона. При n =10 и уровне значимости 5%, 
, 
.
Поскольку 
, то гипотеза о независимости остатков принимается и модель признается адекватной по данному критерию.
г) Случайные отклонения далжны быть независимы от объясняющих переменных.
Так как 
, то 
д) Проверку соответствия распределения остаточной последовательности нормальному закону распределения осуществим с помощью R/S -критерия. формуле:
.
Расчетное значение R/S -критерия сравнивается с табличными значениями (нижней и верхней границами данного отношения).
Нижняя и верхняя границы отношения при уровне значимости 
равны соответственно 2,67 и 3,57.
Расчетное значение отношения попадает в интервал между критическими границами, следовательно, с заданным уровнем значимости гипотеза о нормальности распределения принимается.
