Задача. Згідно з вибіркою статистичних даних за 8 років, які характеризують обсяг виробленої продукції (Y), тис. т в залежності від вартості основних засобів (Х1), тис. грн. та чисельності працюючих (Х2), чол. побудувати лінійну регресійну модель виду:
Y = b0 + b1 X1 + b2 X2.
Знайти векторну оцінку b* за методом найменших квадратів, для цього треба виконати обчислення за формулою (6.1)
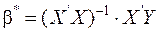
Оцінити тісноту та значимість зв’язку між змінними моделі; проаналізувати достовірність моделі та її параметрів. Відобразити модель на графіку. Застосувати модель для прогнозування розвитку економічних процесів. Виконати економічний аналіз отриманих результатів.
Вихідні дані для розрахунку в табл. 6.1.
Таблиця 6.1
| Спостереження | обсяг виробленої продукції, тис. т | вартість основних засобів, тис. грн. | чисельність працюючих, чол. |
| Y | Х1 | Х2 | |
| 4,2 | |||
| 5,3 | |||
| 6,5 | |||
| 38,2 | 5,8 | ||
| 38,5 | 6,9 | ||
| 40,2 | 5,9 | ||
| 41,1 | 7,2 | ||
| 48,5 | 14,2 | ||
| Середні значення | 39,06 | 7,0 |
Знайти векторну оцінку b* за методом найменших квадратів.
Складемо матрицю X. Перший її стовпчик містить лише одиниці (він відповідає незалежній змінній Х0 – вільному членові); інші стовпчики є відповідно векторами Х1, Х2.
| Матриця Х | |||
| 4,2 | |||
| 5,3 | |||
| 6,5 | |||
| Х = | 5,8 | ||
| 6,9 | |||
| 5,9 | |||
| 7,2 | |||
| 14,2 |
| Матриця Y | |
| Y = | 38,2 |
| 38,5 | |
| 40,2 | |
| 41,1 | |
| 48,5 |
Далі виконуємо операції над матрицями відповідно формули (6.1).
| =ТРАНСП(C29:E36) | ||||||||
| Х′ = | 4,2 | 5,3 | 6,5 | 5,8 | 6,9 | 5,9 | 7,2 | 14,2 |
Транспонування матриці просто реалізувати за допомогою “майстра функцій f ” (операція ТРАНСП(.) у категорії “Ссылки и массивы“). Звернення до математичних та статистичних функцій Excel.
=МУМНОЖ(B41:I43;C29:E36)
| 8,0 | 56,00 | ||
| Х′ × Х = | 56,00 | 457,52 | 1304,60 |
| 1304,60 | 4022,00 |
Функція Microsoft Excel МУМНОЖ(. , .) – знаходить добуток матриць.
Для цього треба:
1) відмітити поле, де буде знаходитись результат добутку матриць;
2) ввійти у "майстер функцій f ". У категоріях вибираємо "математичні", а в функціях – МУМНОЖ. Вводимо адреси матриць, добуток яких знаходимо;
3) для того, щоб отримати на екрані значення добутку матриць, натискаємо спершу клавішу F2, а потім Ctrl+Shift+Еnter.
Функція Microsoft Excel МОБР(D46:F48) – знаходить обернену матрицю.
Матриця похибок
| 3,78969 | 0,12007 | –0,20478 | |
| (Х' × Х)–1 = | 0,12007 | 0,03291 | –0,01593 |
| –0,20478 | –0,01593 | 0,01438 |
Функція Microsoft Excel МОБР(.) – знаходить матрицю, обернену до квадратної матриці. Процедура знаходження оберненої матриці аналогічна процедурі мумнож.
=МУМНОЖ(B41:I43;H29:H36)
| 312,5 | |
| Х' × Y = | 2278,91 |
| 7002,7 |
=МУМНОЖ(D51:F53;D56: D58)
| 23,89 | |
| b*= | 0,97 |
| 0,38 |
Отже, наша регресійна модель має вигляд:

|
Далі знаходяться відповідні значення Yрозр за формулою Y=Х×b*(за допомогою "майстра функцій f " МУМНОЖ(.;.) і заносяться до стовпчика "1" табл. 6.2.
Таблиця 6.2
| Yрозр | Yфакт – Yрозр | Yфакт – Yсер | Yрозр – Yсер | |
| 32,92 | 0,08 | –6,06 | –6,146 | |
| 35,89 | 0,11 | –3,06 | –3,175 | |
| 39,33 | –2,33 | –2,06 | 0,272 | |
| 37,89 | 0,31 | –0,86 | –1,169 | |
| 38,97 | –0,47 | –0,56 | –0,097 | |
| 38,75 | 1,45 | 1,14 | –0,312 | |
| 40,40 | 0,70 | 2,04 | 1,334 | |
| 48,36 | 0,14 | 9,44 | 9,294 | |
| 8,399 | 145,96 | =СУММКВ(.) |
=МУМНОЖ(C29:E36;D61:D63)
Останній рядок таблиці 6.2 – значення сум квадратів відхилень стовпчиків 2, 3 та 4, які розраховуються за допомогою процедури "майстра функцій f " СУММКВ(.).
2. Проаналізуємо достовірність моделі та її параметрів:
Коефіцієнт детермінації моделі обчислюється за формулою:

В економічних розрахунках вважається прийнятним такий зв’язок між факторами, при якому r2 > 0,7.
Скоригований коефіцієнт детермінації:
 |
Скоригований коефіцієнт детермінації не перевищує одиниці 
Справедлива нерівність: 
0,9194 < 0,94246
Множинний коефіцієнт кореляції R розраховується за формулою:
 ,
,
що свідчить про вельми високий кореляційний зв’язок між вхідними показниками Y та X1 і X2.
Парні коефіцієнти кореляції розраховують за формулою матриці коефіцієнтів парної регресії між змінними:

Елементи нормалізованих векторів розраховують за формулами:



Дисперсії змінних мають такі значення:


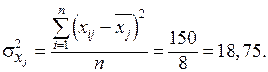
Тоді знаменники для нормалізації кожної змінної будуть такими:
y*: 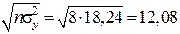 ;
;
xk*:  ;
;
xj*:  .
.
Таблиця 6.3

| 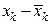
| 
| 
| 
| 
| 
| 
| 
|
| -6,06 | -2,80 | -9,00 | 36,75 | 7,84 | -0,5018 | -0,3459 | -0,7348 | |
| -3,06 | -1,70 | -4,00 | 9,38 | 2,89 | -0,2535 | -0,2100 | -0,3266 | |
| -2,06 | -0,50 | 2,00 | 4,25 | 0,25 | -0,1707 | -0,0618 | 0,1633 | |
| -0,86 | -1,20 | 0,00 | 0,74 | 1,44 | -0,0714 | -0,1482 | 0,0000 | |
| -0,56 | -0,10 | 0,00 | 0,32 | 0,01 | 0,0 | -0,0466 | -0,0124 | 0,0000 |
| 1,14 | -1,10 | 2,00 | 1,29 | 1,21 | 4,0 | 0,0942 | -0,1359 | 0,1633 |
| 2,04 | 0,20 | 3,00 | 4,15 | 0,04 | 0,1686 | 0,0247 | 0,2449 | |
| 9,44 | 7,20 | 6,00 | 89,07 | 51,84 | 0,7812 | 0,8895 | 0,4899 | |
| Усього | 145,96 | 65,52 |
Матриця нормалізованих змінних:
| -0,5018 | -0,3459 | -0,7348 | |
| -0,2535 | -0,2100 | -0,3266 | |
| -0,1707 | -0,0618 | 0,1633 | |
| X* = | -0,0714 | -0,1482 | 0,0000 |
| -0,0466 | -0,0124 | 0,0000 | |
| 0,0942 | -0,1359 | 0,1633 | |
| 0,1686 | 0,0247 | 0,2449 | |
| 0,7812 | 0,8895 | 0,4899 |
Матриця, транспонована до X*:
| -0,5018 | -0,2535 | -0,1707 | -0,0714 | -0,0466 | 0,0942 | 0,1686 | 0,7812 | |
| X*' = | -0,3459 | -0,2100 | -0,0618 | -0,1482 | -0,0124 | -0,1359 | 0,0247 | 0,8895 |
| -0,7348 | -0,3266 | 0,1633 | 0,0000 | 0,0000 | 0,1633 | 0,2449 | 0,4899 |
Запишемо шукану кореляційну матрицю:
| 0,9347 | 0,8630 | ||
| rxx = | 0,9347 | 0,7323 | |
| 0,8630 | 0,7323 |
Кожний елемент цієї матриці характеризує тісноту зв’язку однієї змінної з іншою.
Оскільки діагональні елементи характеризують тісноту зв’язку кожної змінної з цією самою змінною, то вони дорівнюють одиниці. Решта елементів матриці rххтакі:
 ;
;
 ;
;
 .
.
Вони є парними коефіцієнтами кореляції між змінними.
Користуючись цими коефіцієнтами, можна зробити висновок, що між змінними y та xj – високий зв’язок; між змінними y та xk існує досить високий кореляційний зв’язок
Частинні коефіцієнти кореляції, як і парні, характеризують тісноту зв’язку між двома змінними, але за умови, що решта змінних сталі.
Розрахунок частинних коефіцієнтів кореляції базується на оберненій матриці до матриці rxx (матриця С):
 ,
,
де сkj – елемент матриці С, що міститься в k-му рядку i j-му стовпці;
сkk і сjj – діагональні елементи матриці С.
Розрахуємо матрицю, обернену до матриці rxx:
| 17,379 | –11,35 | –6,69 | |
| C = | –11,345 | 9,56 | 2,79 |
| –6,69 | 2,79 | 4,73 |
Матриця C – симетрична, і її діагональні елементи завжди мають бути додатними.
Визначимо частинні коефіцієнти кореляції:
| r yxk = | 0,8801 |
| r yxj = | 0,7377 |
| r xk xj = | –0,4145 |
Частинні коефіцієнти кореляції характеризують рівень тісноти зв’язку між двома змінними за умови, що решта змінних на цей зв’язок не впливає. Частинні коефіцієнти кореляції за модулем нижчі, ніж коефіцієнти парної кореляції, бо на їхній рівень не впливає решта змінних, які мають зв’язок із цими двома.
Коефіцієнт парної кореляції ryxk = 0,88, тому можна зробити висновок, що рівень тісноти зв’язку між двома змінними (y та xk;) високий за умови, що решта змінних на цей зв’язок не впливає.
Коефіцієнт парної кореляції ryxj = 0,7377 – можна зробити висновок, що рівень тісноти зв’язку між двома змінними (y та xj) високий за умови, що решта змінних на цей зв’язок не впливає.
Перевіримо значимість зв’язку між змінними моделі:

| F0,05табл = | 3,97 |
| F0,05табл < | Fрозр |
Модель приймаємо – припускаємо присутність лінійного зв’язку для рівня надійності р =(1– a) = 0,95.
Стандартні похибки оцінок параметрів з урахуванням дисперсії залишків:


| З матриці похибок: | |
| С00= | 3,78969 |
| С11= | 0,03291 |
| С22= | 0,01438 |



Стандартні помилки параметрів не перевищують абсолютні значення цих параметрів, то це означає, що оцінки параметрів є незміщеними відносно їх істотних значень.
Стійкість оцінок параметрів визначається порівнянням стандартних похибок з абсолютними значеннями оцінок параметрів моделі.
Порівняємо стандартні похибки оцінки з величиною оцінки параметра:

 ,
,








