Силы инерции и моменты пар сил инерции определяются для тех звеньев, массы которых заданы. Инерционные нагрузки определяются в зависимости от характера движения звеньев.
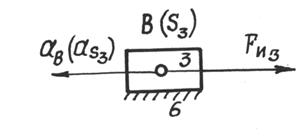 3.1.1. Звено движется поступательно (ползун). В этом случае момент инерции звена МИ3 = 0. Сила инерции
3.1.1. Звено движется поступательно (ползун). В этом случае момент инерции звена МИ3 = 0. Сила инерции  направлена против ускорения центра масс
направлена против ускорения центра масс  (рис. 3.1)
(рис. 3.1)
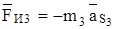 ;
;  ,
,
где mS5 – масса ползуна, кг;
F3 – вес ползуна, Н.
Рис. 3.1
3.1.2. Звено совершает неравномерное вращательное движение (коромысло) вокруг оси, не проходящей через центр тяжести (рис. 3.2 ). В этом слу -
чае на звено действует момент пар сил 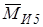 , направленный в сторону, противоположную направлению углового ускорения e5, и сила инерции
, направленный в сторону, противоположную направлению углового ускорения e5, и сила инерции  , направленная в сторону, противоположную вектору абсолютного ускорения центра масс аS5, и приложенная в центре масс звена S5:
, направленная в сторону, противоположную вектору абсолютного ускорения центра масс аS5, и приложенная в центре масс звена S5:
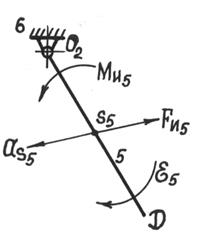
Рис. 3.2
 ;
;  , (3.2)
, (3.2)
где JS5 – момент инерции звена относительно оси, проходящей через центр тяжести, кг×м2;
l5 – длина звена, м.
 3.1.3. Звено совершает плоскопараллельное движение (шатун) В этом случае на звено действует момент пары сил инерции
3.1.3. Звено совершает плоскопараллельное движение (шатун) В этом случае на звено действует момент пары сил инерции 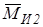 , направленной в сторону, противоположную угловому ускорению e2, и сила инерции
, направленной в сторону, противоположную угловому ускорению e2, и сила инерции 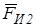 , направленная противоположно вектору абсолютного ускорения центра масс звена
, направленная противоположно вектору абсолютного ускорения центра масс звена  и приложенная в центре звена (рис. 3.3).
и приложенная в центре звена (рис. 3.3).
Для удобства силового расчета механизма момент пары сил инерции 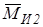 представляем эквивалентной парой сил, направление вращения корой совпадает с направлением момента. Плечо пары сил принимаем равным длине звена АВ. В точке А перпендикулярно оси звена прикладываем силу
представляем эквивалентной парой сил, направление вращения корой совпадает с направлением момента. Плечо пары сил принимаем равным длине звена АВ. В точке А перпендикулярно оси звена прикладываем силу 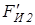 вверх, а в точке в – силу
вверх, а в точке в – силу  вниз. Сила, Н,
вниз. Сила, Н,
Рис. 3.3
 , (3.3)
, (3.3)
Полученная пара сил заменяет действие момента пар, сил инерции 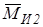 , поэтому момент
, поэтому момент 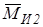 на рис. 3.3 зачеркнут.
на рис. 3.3 зачеркнут.
Определение реакций в кинематических парах
Структурных групп
Рассмотрим механизм, изображенный на рис. 2.3, а.
П р и м е р 5. Произвести кинетостатическое исследование механизма по условию примера 2. Дополнительные данные для расчета: Fп.с = 1000 Н;
q = 0,10 Н/мм,
где Fп.с - сила полезного сопротивления, приложенная к коромыслу, направлена против скорости vD;
q – вес одного миллиметра длины звена, Н/мм.
Р е ш е н и е. Для того чтобы определить значения и направления сил инерции, надо знать ускорения и массы звеньев. Ускорения известны из плана ускорений механизма. Определим вес каждого звена, Н:
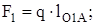
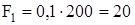 ;
;
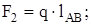
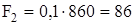 ; (3.4)
; (3.4)
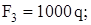
 .
.
(если в условии не задана величина веса или масса ползуна);
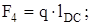
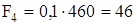 ;
;
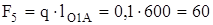 .
.
Определяем массу каждого звена, кг:

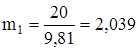 ;
;
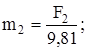
 ;
;

 ; (3.5)
; (3.5)
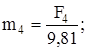
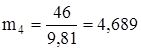 ;
;
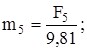
 .
.
Определяем силу инерции каждого звена, Н:
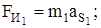
 ;
;
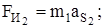
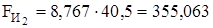 ;
;
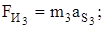
 ; (3.6)
; (3.6)
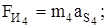
 ;
;

 .
.
Определяем момент пары сил инерции для звеньев АВ, CD и O2D, совершающих сложные движения:
звено АВ – 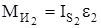 ;
;

 кг×м2;
кг×м2;
 с-2;
с-2;
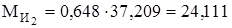 Н×м;
Н×м;
звено CD – 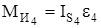 ;
;
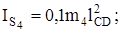
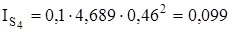 кг×м2;
кг×м2;
 с-2.
с-2.
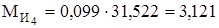 Н×м;
Н×м;
звено О2D –  ;
;
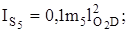
 кг×м2;
кг×м2;
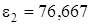 с-2.
с-2.
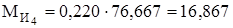 Н×м.
Н×м.
Силовой расчет механизма начинаем с наиболее удаленной от ведущего звена группы Ассура 4 – 5 (CDO2), состоящей из звеньев 4 и 5, трех вращательных кинематических пар – С1D1O2.
Группу CDO2 вычерчиваем отдельно в масштабе схемы механизма и в том же положении (рис. 3.4, а). Прикладываем к ней вместо связей две реакции:
одну F65 – во вращательной паре O2, другую F24 представляем в виде двух составляющих: тангенциальной 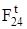 , направленной перпендикулярно к оси звена CD, и нормальной
, направленной перпендикулярно к оси звена CD, и нормальной 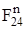 - вдоль звена CD. Реакцию F65 представляем также в вив в виде двух составляющих:
- вдоль звена CD. Реакцию F65 представляем также в вив в виде двух составляющих: 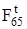 - направлена перпендикулярно к звену DО2,
- направлена перпендикулярно к звену DО2,  - вдоль звена.
- вдоль звена.
Кроме этого прикладываем силы веса F4 и F5 в центрах тяжести и силы инерции:  - против ускорения тяжести S4;
- против ускорения тяжести S4;  - против ускорения
- против ускорения  . Момент инерции
. Момент инерции 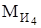 заменяем парой сил:
заменяем парой сил:  , приложенной в точке С против направления углового ускорения звена 4 (e4), и
, приложенной в точке С против направления углового ускорения звена 4 (e4), и  - в точке D. Аналогично поступаем со звеном DO2: момент инерции
- в точке D. Аналогично поступаем со звеном DO2: момент инерции 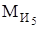 заменяем парой сил
заменяем парой сил 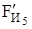 и
и 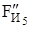 , приложенной против направления углового ускорения звена 5 (e5) в точках O2 и D.
, приложенной против направления углового ускорения звена 5 (e5) в точках O2 и D.
П р и м е ч а н и е. На звене O2D, совершающем вращательное движение относительно оси, не проходящей через центр тяжести, допускается силу инерции  прикладывать не в центре тяжести S5, а в центре качения звена (точка К), расположенном на расстоянии
прикладывать не в центре тяжести S5, а в центре качения звена (точка К), расположенном на расстоянии 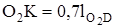 . В этом случае
. В этом случае 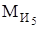 определять не надо и заменяющую пару сил
определять не надо и заменяющую пару сил 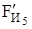 и
и 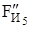 не прикладывать.
не прикладывать.
Для определения реакций в кинематических парах составляем векторное уравнение равновесия сил, действующих на группу 4 – 5 по порядку звеньев:
 . (3.7)
. (3.7)
Силы  ,
,  ,
, 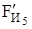 и
и 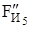 в уравнение не вписаны, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга, но для определения
в уравнение не вписаны, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга, но для определения 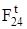 эти силы надо знать, Н:
эти силы надо знать, Н:
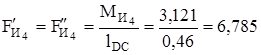 ;
;
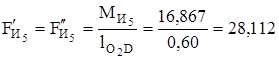 .
.
Определяем 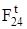 , входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено CD, относительно точки D:
, входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено CD, относительно точки D:
 ; (3.8)
; (3.8)
 Н.
Н.
Поскольку составляющую 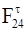 получилась со знаком «минус», то это значит, что ее действительное направление противоположно выбранному
получилась со знаком «минус», то это значит, что ее действительное направление противоположно выбранному
(см. рис. 3.4, а). На схеме группы Асура первоначальное направление зачеркнуто.
Определяем 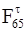 , входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено DO2, относительно точки D:
, входящую в уравнение равновесия, составив уравнение моментов всех сил, действующих на звено DO2, относительно точки D:
 (3.9)
(3.9)
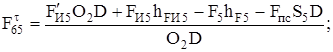
 Н.
Н.
В этом случае знак составляющей 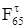 не изменяется, значит, на схеме группы Ассура направление
не изменяется, значит, на схеме группы Ассура направление 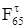 сохраняется.
сохраняется.
Исходя из значений сил, входящих в уравнение равновесия:
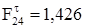 Н;
Н; 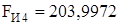 Н;
Н;  Н;
Н; 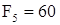 Н;
Н;
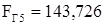 Н;
Н;  Н;
Н;  Н,
Н,
задаемся масштабом плана сил:  , Н/мм.
, Н/мм.
Максимальной силой является сила полезного сопротивления, которую в примере изобразим вектором длиной 100 мм (р е к о м е н д а ц и я: максимальную силу изображать вектором в пределах 150 – 200 мм).
Получаем масштаб плана сил, Н × мм-1:
 .
.
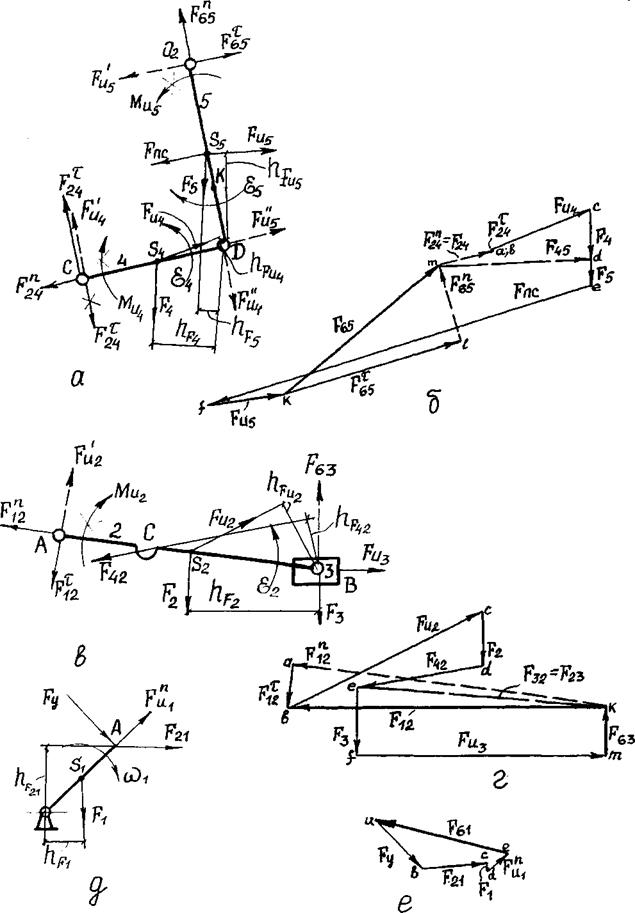
Рис.3.4
Вычисляем длины векторов, мм, изображающих эти силы, поделив их численные значения на масштаб:
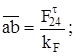
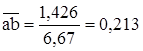 ;
; 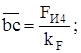
 ;
;
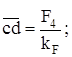
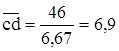 ;
; 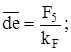
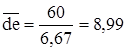 ;
;
 (задались)
(задались) 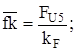
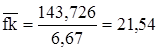 ;
;
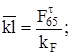
 ;
;
От произвольной точки а – начала плана сил (см. рис. 3.4, е) – параллельно силе 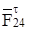 откладываем вектор
откладываем вектор 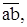 изображающий эту силу (в примере
изображающий эту силу (в примере 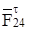 мала, выражена точкой); от конца вектора
мала, выражена точкой); от конца вектора 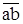 параллельно силе
параллельно силе 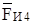 откладываем в том же направлении вектор
откладываем в том же направлении вектор 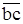 и далее векторы всех сил. Через точку а параллельно звену CD проводим линию действия
и далее векторы всех сил. Через точку а параллельно звену CD проводим линию действия 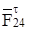 , а через точку l параллельно звену O2D – линию действия силы
, а через точку l параллельно звену O2D – линию действия силы 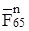 . Точка пересечения m этих линий определяет силы
. Точка пересечения m этих линий определяет силы 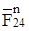 ,
, 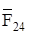 ,
, 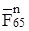 ,
,  , Н:
, Н:
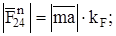
 ;
;
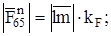
 ; (3.10)
; (3.10)
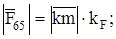
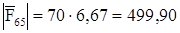 .
.
Для определения реакции в шарнире D составляем уравнение равновесия сил, действующих на звено 4:
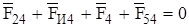 . (3.11)
. (3.11)
Векторы сил 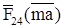 ,
, 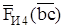
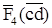 уже есть на плане сил, поэтому реакция
уже есть на плане сил, поэтому реакция 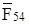 со стороны звена 5 на звено 4) будет замыкающим вектором
со стороны звена 5 на звено 4) будет замыкающим вектором 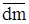 :
:
 Н.
Н.
Реакция со стороны звена 4 на звено 5 равна по значению и противоположна по направлению  :
:
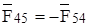 . (3.12)
. (3.12)
Далее следует отсоединить группу Ассура АВ, состоящую из звеньев 2 и 3, двух вращательных кинематических пар – А и В и одной поступательной (при движении ползуна по направляющей), вычертить ее в масштабе схемы на рис. 2.3. В соответствующих точках приложить действующие силы: 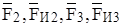 . Реакцию в шарнире А представить в виде двух составляющих –
. Реакцию в шарнире А представить в виде двух составляющих –  и
и 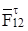 , а в поступательной паре – в виде F65, перпендикулярной линии хода ползуна. Реакцию со стороны звена 4 на звено 2, полученную из плана сил группы Ассура CDO2,
, а в поступательной паре – в виде F65, перпендикулярной линии хода ползуна. Реакцию со стороны звена 4 на звено 2, полученную из плана сил группы Ассура CDO2, 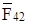 приложить в обратном направлении в точке С звена 2
приложить в обратном направлении в точке С звена 2 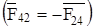 .
.
Составляем векторное уравнение равновесия сил, действующих на группу Ассура 2 – 3 (АВ), по порядку звеньев:
 . (3.13)
. (3.13)
Силы  и
и  в уравнение не вписываем, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга. Но для определения
в уравнение не вписываем, так как это уравнение решается построением плана сил и они взаимно уравновешивают друг друга. Но для определения  эти силы надо знать, определяем их:
эти силы надо знать, определяем их:

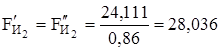 Н.
Н.
Из уравнения моментов относительно точки В для звена 2 определяем составляющую  , Н:
, Н:
 , (3.14)
, (3.14)
отсюда
 ; (3.15)
; (3.15)
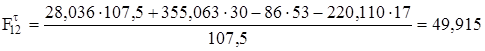 .
.
Размеры плеч  снимаем с чертежа в миллиметрах. Поскольку знак составляющей
снимаем с чертежа в миллиметрах. Поскольку знак составляющей  не изменился, ее действительное направление соответствует выбранному (см. рис. 3.4, е).
не изменился, ее действительное направление соответствует выбранному (см. рис. 3.4, е).
Выписав значения всех сил, действующих на группу Ассура, по максимальной из них задаемся масштабом:
 = 49,915 Н;
= 49,915 Н;  Н; F2 = 86 Н; F42 = 220,11 Н;
Н; F2 = 86 Н; F42 = 220,11 Н;
F3 = 100 Н; 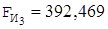 Н.
Н.
Максимальную силу 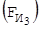 изобразим вектором, длина которого 78,49 мм (произвольно), тогда
изобразим вектором, длина которого 78,49 мм (произвольно), тогда
 Н/мм.
Н/мм.
Вычисляем длины векторов, изображающих эти силы, мм:

 ;
; 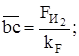
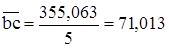 ;
;
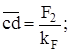
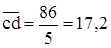 ;
; 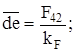
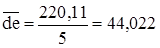 ;
;
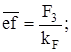
 ;
; 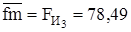 (задались).
(задались).
Строим план сил (рис. 3.4, г) из которого определяем нормальную составляющую и результирующую давления в шарнире А и реакцию со стороны стойки на ползун 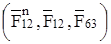 , Н:
, Н:
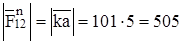 ;
;
 ; (3.16)
; (3.16)
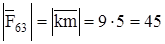 ;
;
Для определения реакции в шарнире В ползуна составим уравнение равновесия сил, действующих на звено 2:
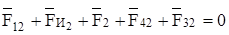 .
.
Векторы сил 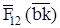 ,
, 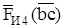
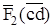
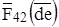 уже есть на плане сил; соединив точки e и k, получаем реакцию
уже есть на плане сил; соединив точки e и k, получаем реакцию  , действующую со стороны звена 3 на звено 2, Н:
, действующую со стороны звена 3 на звено 2, Н:

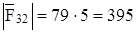 .
.
Реакция со стороны звена 2 на звено 3 равна по значению и противоположна по направлению  :
:
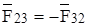 .
.
Расчет ведущего звена производим с учетом всех действующих на него сил: веса 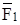 , инерции
, инерции  , со стороны стойки – реакция
, со стороны стойки – реакция 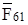 . Кроме этих сил в точку А кривошипа перпендикулярно к оси звена приложим уравновешивающую силу
. Кроме этих сил в точку А кривошипа перпендикулярно к оси звена приложим уравновешивающую силу  . Силы
. Силы 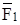 ,
,  и
и 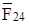 известны по значению и направлению, а силы
известны по значению и направлению, а силы 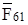 и
и  не известны (см. рис. 3.4, б).
не известны (см. рис. 3.4, б).
Для определения значения  составляем уравнение моментов всех сил, действующих на звено 1, относительно точки О1:
составляем уравнение моментов всех сил, действующих на звено 1, относительно точки О1:
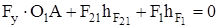 ; (3.17)
; (3.17)
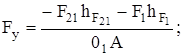
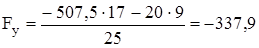 Н.
Н.
Определяем реакцию 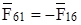 по значению и направлению путем построения плана сил согласно векторному уравнению:
по значению и направлению путем построения плана сил согласно векторному уравнению:
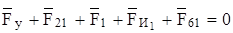 . (3.18)
. (3.18)
Выписав значения всех сил, Н, по максимальной из них задаемся масштабом:
Fу = 337,9; F21 = 507,5; F1 =20; 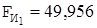 .
.
Изобразим F21 = 507,5 Н вектором длиной 50,75 мм, тогда
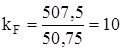 Н/мм.
Н/мм.
Вычисляем длины векторов всех сил для плана, мм:

 ;
; 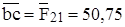 (задались);
(задались);
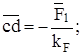
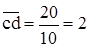 ;
; 
 .
.
Соединив точки f и a получаем реакцию в шарнире О1 (со стороны звена 6 на звено 1):
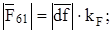
 Н.
Н.
П р и м е ч а н и е. Полученные значения всех сил, действующих на звенья механизма и реакций во всех кинематических парах рекомендуется, свести в таблицу.
4. Расчет кривошипно-шатунного механизма (кшм)
на эвм
Задачей расчета являются определение кинематических и силовых параметров механизма, построение планов скоростей, ускорений, сил и построение крайних положений звеньев механизма по заданным параметрам.
Схема алгоритма расчета КШМ приведена на рис. 4.1
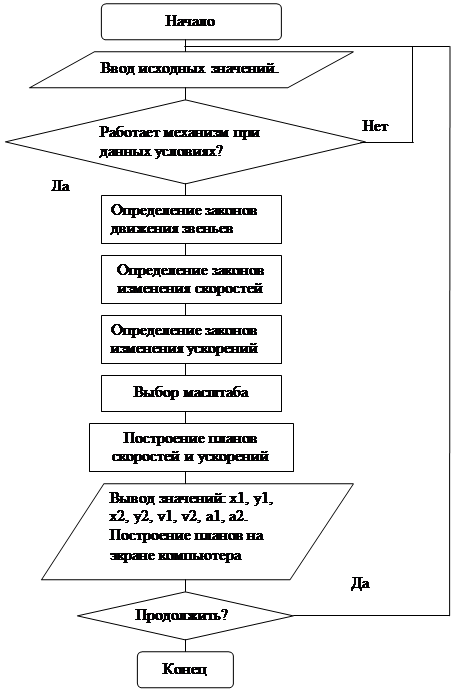 |
Рис. 4.1
Для удобства написания программы в ней были применены идентификаторы, приведенные в таблице.
Таблица
Идентификаторы и соответствующие им величины
| Идентифи-катор | Обозначение величины. | Единица величины | Наименование величины |
| а | j | градус | Угол, задающий начальное положение кривошипа |
| x1, x2, y1, y2 | x, y | м | Координаты соответствующих звеньев |
| v1,v2 | v | м/с | Скорости точек соответствующего звена |
| a1,a2 | a | м/с2 | Ускорения соответствующих точек звена |
На основе результатов, полученных с помощью ЭВМ, сделать сравнение аналитического и графического метода решения задач. Сравнить полученные результаты с результатами расчета, сделанного в ручном режиме для исходных данных, соответствующего варианта.






