Кинематическое исследование состоит в изучении движения отдельных точек (звеньев) механизма независимо от сил, вызывающих это движение. Основной задачей кинематического исследования является определение:
1) положения всех звеньев при любом мгновенном положении ведущего звена;
2) траектории движения точек звеньев;
3) линейных скоростей и ускорений точек звеньев;
4) угловых скоростей и ускорений точек звеньев.
Существует три основных метода кинематического исследования механизмов:
графиков (наименее точный и наименее трудоемкий);
планов (более точный и более трудоемкий);
аналитический (самый точный и самый трудоемкий).
Графический метод, основанный на построении графиков законов движений с применением графического дифференцирования, обладает простотой и наглядностью, но имеет недостаточную точность, поэтому в инженерных расчетах применяют графоаналитический метод. Он дает удовлетворительную точность, но требует аккуратное выполнение графических работ и соблюдение масштаба.
Под масштабом подразумевается отношение действительной величины, выраженной в соответствующих единицах, к длине отрезка, изображающего эту величину, выраженной в миллиметрах. При построении кинематических схем и планов положений механизмов (рис. 2.1) определяется масштаб длин, показывающий число метров натуральной величины, соответствующей одному миллиметру чертежа, м/мм:
, (2.1)
где lO1A – действительная длина кривошипа, м;
О1А – длина отрезка, изображающего кривошип на чертеже, мм.
|
Рис. 2.1
При построении планов скоростей и ускорений на чертеже приходится откладывать значения скорости и ускорения в некотором масштабе. Например, если вектор вычисленной скорости точки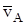 
, м/с, на плане скоростей изображен в виде отрезка 
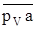произвольной длинны, мм, то, поделив значение скорости 
на длину этого отрезка, найдем масштаб плана скоростей, м/с × мм-1:
Аналогично найдем масштаб плана ускорений, м/с × мм-1:
где аА – вычисленная величина ускорения точки А, м/с2;
– масштабное значение ускорения точки А, мм.
Истинные значения скорости и ускорения любой точки механизма получают из их масштабных значений путем умножения последних на соответствующий масштаб.
Построение планов положений механизмов
Планом положения механизма называется чертеж, изображающий расположение его звеньев в какой-то определенный момент движения. Отсюда следует, что план положения представляет собой кинематическую схему механизма, вычерченную для заданного положения механизма.
Планы положений механизмов, включающих в себя двухповодковые группы, строятся методом засечек.
Рассмотрим это на примере.
П р и м е р 2. Построить положения механизма (см. рис. 2.1) для заданного угла поворота j1 ведущего звена при lO1A = 0,200 м; lAB = 0,860 м;
lAC = 0,360 м; lCD = 0,460 м; lDoe = 0,600 м; а = 0,770 м; b = 0,760 м; j1 = 135°.
Р е ш е н и е. Для построения плана принимаем, что длину кривошипа lO1A на схеме будет изображать отрезок О1А, длина которого равна 25 мм. Тогда масштаб плана 
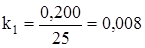м/мм. Затем вычисляем длины других отрезков, изображающих звенья механизма, которые будем откладывать на чертеже, мм:
; 
;
|
|
;
; 
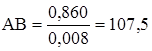Построение плана начинаем с нанесения элементов неподвижного звена (точек опор О1 и О2 и линии хода ползуна y – y). Под углом j1 = 135° к x – x из точки О1 проводим ось ведущего звена и от точки О1 откладываем на ней отрезок О1А, равный длине кривошипа.
Затем определяем положение точки В. Для этого из точки А радиусом АВ делаем засечку на линии хода ползуна y – y. На звене АВ находим положение точки С. Для того чтобы найти положение точки D, проводим дуги: из
точки С – радиусом CD, из точки О2 – радиусом O2D. Точка их пересечения будет точкой D.
