планов ускорений
При помощи планов ускорений можно найти ускорения любых точек механизма. Для построения планов ускорений по аналогии с планами скоростей следует пользоваться их свойствами. Свойства такие же, как и у планов скоростей (см. подразд. 2.5), кроме третьего, где фигура, подобная одноименной жесткой фигуре на плане положений механизма, повернута на угол (180° – j¢) в сторону мгновенного ускорения e данного звена:
. (2.14)
Поскольку полные относительные ускорения состоят из геометрической суммы тангенциальных и нормальных составляющих, то концы векторов абсолютных ускорений обозначают буквами, соответствующими названию точек.
Определение ускорений рассмотрим также на примере механизма, представленного на рис. 2.3, а.
П р и м е р 4. Методом планов ускорений определить абсолютные и относительные ускорения точек звеньев и угловые ускорения звеньев механизма. Данные взять из условия примера 2.
Р е ш е н и е. Считая известными ускорения шарнирных точек (аО1 = аО2 = 0), помещаем их на плане ускорений в полюсе рa. Звено О1А вращается равномерно, поэтому точка А имеет только нормальное ускорение 
, которое направлено по звену О1А к центру вращения О1 (рис. 2.3, в). Определяем его по формуле:
; 
м/с2. (2.15)
Принимаем (произвольно) длину отрезка 
, изображающего вектор ускорения 
точки А, равной 98,596 мм. Тогда масштаб плана ускорений, м/с2×мм-1,
; 
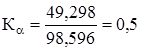. (2.16)
Из полюса плана ра откладываем параллельно звену О1А в направлении от А к О1.
Рассматривая движения точки В со звеном АВ, составляем векторное уравнение:
. (2.17)
В этом уравнении ускорение точки А известно по величине и по направлению. Определяем нормальное ускорение точки В относительно А:
м/с2. (2.18)
На плане ускорений 
можно выразить отрезком 
мм и отложить его параллельно звену АВ на плане из точки а в направлении от В к А (a1 n1), а затем из точки n1 перпендикулярно звену АВ провести линию действия тангенциального ускорения до пересечения с линией хода ползуна (это и будет точка b).
Определяем ускорения точки В, м/с2:
;
(2.19)
.
Положение точки С на плане ускорений находим по свойству подобия (из пропорции):
; 
. (2.20)
Соединив ее с полюсом, определяем ускорение точки С, м/с2:
. 
.
Для определения ускорения точки D рассматриваем движения точки D со звеньями СD и DO2. Составляем векторные уравнения:
;
.
Определяем нормальные ускорения (ускорение точки С известно по величине и по направлению, а ускорение аО2 = 0), м/с2:
;
;
От точки С плана ускорений параллельно звену DC в направлении от точки С к точке D откладываем вектор 
, изображающий ускорение 
, длина которого
мм. (2.21)
Из точки О2 плана ускорений (из полюса ра) параллельно звену DO2 в направлении от D к О2 откладываем вектор 
, изображающий ускорение 
, величина которого
мм.
Через точку n2 проводим перпендикулярно звену CD линию действия тангенциального ускорения 
до пересечения с линией действия 
, проведенной из точки n3 перпендикулярно звену O2D. На их пересечении получится точка d – конец вектора 
, изображающего ускорение 
точки D механизма:
м/с2.
Определяем тангенциальные ускорения и относительные во вращении вокруг точек С и О2, м/с2:
;
;
;
.
Из третьего свойства планов ускорений (свойства подобия) определяем места положений точек центров тяжести, а затем величины ускорений:
; 
;
;
;
;
.
Определяем угловые ускорения звеньев.
Угловое ускорение e1 ведущего звена О1А, совершающего равномерное движение, равно нулю.
Угловое ускорение звена 2
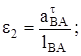
с-2.
Для определения направления углового ускорения e2 звена 2 надо мысленно перенести вектор 
тангенциального ускорения 
в точку В. В направлении этого вектора точка В вращается относительно точки А против часовой стрелки (см. рис. 2.3).
По аналогии определяем значения и направления угловых ускорений звеньев 4 и 5, с-2:
(против часовой стрелки);
(по часовой стрелке).
Примечание. Полученные значения линейных и угловых ускорений и скоростей всех точек механизма рекомендуется свести в таблицу.
3. СИЛОВОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМОВ
В задачу силового исследования входит определение:
1) сил, действующих на звенья механизма;
2) реакций в кинематических парах;
3) уравновешивающей силы (момента).
Силовой анализ основан на принципе Даламбера. Сущность его заключается в том, что каждое звено может рассматриваться в условном статическом равновесии, если к нему помимо всех действующих внешних сил приложить инерционную нагрузку в виде силы инерции и момента пары сил инерции. При этом условии для каждого звена справедливы равенства:
, (3.1)
поэтому неизвестные силы (реакции в кинематических парах) могут определяться методом статики.
Для проведения силового анализа кинематическая цепь должна быть статически определимой, т. е. число неизвестных параметров реакций должно быть равно количеству уравнений статики, которые можно составить для их определения.
Начинать силовой анализ необходимо с наиболее удаленной от ведущего звена структурной группы.
