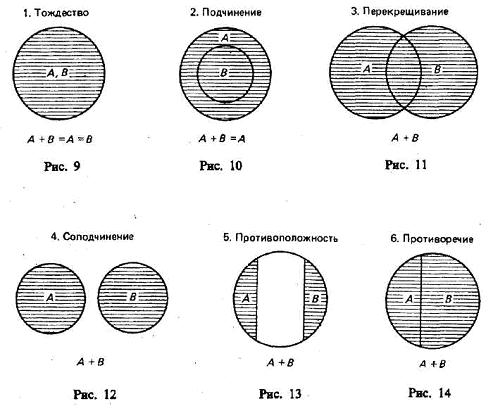
Предположим, мы знаем, что некто - ученый, и хотим уточнить наши знания о нем. Уточняем: это - русский ученый, выдающийся русский ученый, выдающийся русский ученый-химик, создатель Периодической системы элементов. Произведенная логическая операция есть операция ограничения понятия. Приведем еще пример. Дано понятие населенный пункт. Ограничив его, получим понятия: город, столица, столица Российской Федерации. Мы видим, что при ограничении происходит переход от понятия с большим объемом к понятию с меньшим объемом, т.е. от рода к его виду и от вида к подвиду. При этом добавляются новые признаки, позволяющие сузить объем понятия. Ограничение - это логическая операция перехода от родового понятия к видовому путем добавления к содержанию данного родового понятия видообразующих признаков. Пределом ограничения является единичное понятие: в приведенных выше примерах это были понятия: создатель Периодической системы элементов и столица Российской Федерации. Обратная ограничению операция обобщения понятия состоит в переходе от видового понятия к его родовому понятию, т.е. от понятия с меньшим объемом к понятию с большим объемом. Эта операция совершается путем отбрасывания видообразующего признака (признаков). Например, обобщая понятие сиамская домашняя кошка, получим следующие понятия: домашняя кошка, кошка, млекопитающее животное, позвоночное животное, животное, организм. Обобщение - это логическая операция перехода от видового понятия к родовому путем отбрасывания от содержания данного видового понятия его видообразующего признака (признаков). Пределом обобщения являются универсальные понятия. В основе операций обобщения и ограничения лежит закон обратного отношения между содержаниями и объемами понятий.
11.Операции с классами (объемами понятий): пересечение, объединение, вычитание и дополнение.
Операции с классами — это такие логические действия, которые приводят нас к образованию нового (в общем случае) класса.
Существуют следующие операции с классами: объединение, пересечение, вычитание, дополнение.
Объединение («сложение») классов
Объединение (или сумма) двух классов — это класс тех элементов, которые принадлежат хотя бы к одному из этих двух классов17: Объединение обозначается: или Объединение класса четных чисел с классом нечетных чисел дает класс целых чисел. Объединив класс поэтов и класс советских поэтов, получим класс поэтов.
При выражении операции объединения классов пользуются обычно союзом «или» в не исключающем смысле. Например, говоря, что некто — член волейбольной или гимнастической секции, мы не исключаем того, что этот человек может быть одновременно членом обеих секций.
В языке существует и такое употребление союза «или», при котором этот союз понимается в строго разделительном смысле,
например: «Данный глагол первого или второго спряжения». Соответствующая операция над классами называется симметрической разностью и в наиболее интересном случае иллюстрируется графически так, как это изображено на рис. 8.

Класс, составляющий симметрическую разность классов А и В, на чертеже выделен штриховкой. Симметрическая разность не содержит общих членов классов А и В.
При объединении могут встретиться следующие 6 случаев (рис. 9—14).
Пересечение («умножение») классов
Общей частью, или пересечением, двух классов называется класс тех элементов, которые содержатся в обоих данных множествах, т. е. это множество (класс) элементов, общих обоим множествам18. Пересечение обозначается или — пустое множество. При пересечении могут встретиться следующие 6 случаев (рис. 15—20, где результат пересечения заштрихован).

Например, операция пересечения классов «школьник» (А) и «футболист» (В) заключается в нахождении таких людей, которые одновременно являются и школьниками, и футболистами. Это изображено на рис. 17, где общая часть классов А и В заштрихована.

Операция вычитания классов дает класс, состоящий из элементов, исключающих элементы вычитаемых классов. Вычитая, например, элементы класса «следователь» (А) из класса «юрист» (В), получаем класс юристов не-следователей (рис. 16). Вычитая элементы класса «юрист» (А) из класса «депутат Государственной Думы» (В), получаем класс депутатов Государственной Думы, не являющихся юристами. Множество, полученное в результате вычитания классов, заштриховывается (рис. 17).
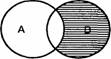
Рис 17
Образование дополнения (отрицание). Дополнением к классу А называется класс не-А (А'), который при сложении с А образует универсальную область. Эта область представляет собой универсальный класс и обозначается знаком 1. Чтобы образовать дополнение, нужно класс А исключить из универсального класса: 1 - А = А'. Образование дополнения состоит, таким образом, в образовании нового множества путем исключения данного множества из универсального класса, в который оно входит. Так, исключая множество адвокатов из универсального класса юристов, образуем дополнение: множество юристов-неадвокатов. В своей сумме оба понятия образуют весь универсальный класс, соответствующий понятию «юрист» (рис. 20).

Рис. 20






