Для отыскания корней на отрезке используются функция root(), для которой требуется задать начальное приближение или отрезок локализации корня. Повышение точности представления результатов решения задачи обеспечивается посредством меню Формат à Результат.
Задание 5. Определение корней полинома
Условие задания 5
Найти корни полинома с помощью функции polyroots(). Полученные действительные корни проверить графически, построив график функции y=f(t) в декартовой системе координат. Задачи приводятся в таблице 10.
Таблица 10.
Условия задач для задания 5
| № задачи | Выражение | № задачи | Выражение |

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
| ||
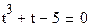
| 
| ||

| 
| ||
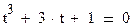
|
Рекомендации по выполнению задания 5
Для нахождения корней полинома применяется функция polyroots(V). гдеV – вектор коэффициентов при неизвестных. Функция позволяет найти как действительные, так и комплексные корни полинома. Для оценки результатов решения задачи, строиться график функции в декартовой системе координат и оценивается правильность нахождения действительных корней полинома.
Задание 6. Решение систем нелинейных уравнений
Условие задания 6
Решить систему нелинейных уравнений с помощью блока given…find. Отобразить результаты с точностью до 7 знаков после десятичной точки. Рассчитать невязку (погрешность вычислений) ERR.. Задачи приводятся в таблице 11.
Таблица 11
Условия задач для задания 6
| № задачи | Выражение | № задачи | Выражение |

| 
| ||
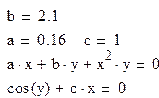
| 
| ||

| 
| ||

| 
| ||

|
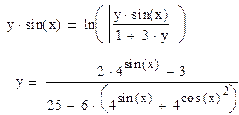
| ||

| 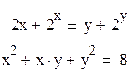
| ||

| 
| ||
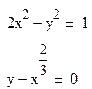
|
Рекомендации по выполнению задания 6
Для решения системы нелинейных уравнений используется блок given…find. При применении бока задаются начальные приближения искомых неизвестных. В данной задаче предлагается исследовать влияние начальных значений на точность результатов решения задачи. Для чего требуется произвести двойной расчет при различных начальных значениях и представить результаты вычислений с точностью до 7 знаков после десятичной точки.
Задание 7. Операции с векторами и матрицами
Условие задания 7
Создать матрицы А и В размерностью 4 х 4 и вектор – столбец d с четырьмя элементами. Заполнить матрицы и вектор значениями, каждое из которых вычисляется по формуле. Ввести значение константы n, которая равна номеру задачи для выбранного варианта задания 7 темы «Mathcad».
Для матрицы А

для матрицы В

для вектора d

для константы n
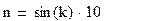
где
x - номер столбца; y – номер столбца, для вектора d значение у задается = 1;
k - номер варианта.
Выполнить указанные ниже операции над матрицами, вектором и константой.
а) А+В; б) А–B; в)А*В; г) В*А; д) А*d; е)n* B; ж)n* d; з) AT; и) В 2; к) А -1; л) B -3;
Для матрицы А определить минимальный и максимальный элемент матрицы. Вычислить среднее значение всех элементов матрицы В. Для каждого номера задачи вычислить матричное выражение (таблица 12) по частям и по единой формуле. Результаты сравнить.
Таблица 12.
Условия задач для задания 7
| № варианта | Выражение |
| 2*(А+В)*(2*В-А) | |
| 3*А – (А+2*В)*В | |
| 2*(А-В)*(А2 + В) | |
| (А2 –В2) * (А +В) | |
| (А – В2)* (2*А + В) | |
| (А – В)*А + 2* В2 | |
| 2*(А -3*В) + А* В | |
| (А-В)*А+ 3*В | |
| 2*А – (А2+В)*В | |
| 3*(А2 – В2) – 2*А*В | |
| (2*А-В)*(3*А+В) -2*А2 | |
| А*(А2-В)- 2*(В+А)*В | |
| (А +В)*А–В*(2*А +3*В) | |
| А*(2*А +В)-В*(А-В) | |
| 3*(А+В)*(А*В-2*А) |






