Ориентированное дерево представляет собой ориентированный граф без циклов, в котором полустепень захода каждой вершины, за исключением одной (например, вершины х1 ), равна единице, а полустепень захода вершины х1(называемой корнем этого дерева) равна нулю.
На рисунке 11 показан граф, который является ориентированным деревом с корнем в вершине х1. Из приведенного определения следует, что ориентированное дерево с п вершинами имеет n-1 дуг и связно. Также очевидно, что не всякий ориентированный граф содержит основное ориентированное дерево. Это подтверждает граф, изображенный на рисунке 12.
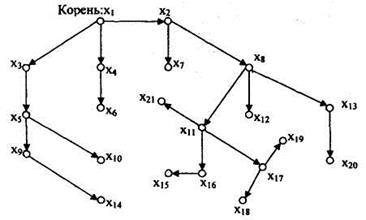
Рисунок 11 - Ориентированное дерево

Рисунок 12 - Граф без ориентированного остовного графа
Следует отметить, что неориентированное дерево можно преобразовать в ориентированное: надо взять его произвольную вершину в качестве корня и Ребрам приписать такую ориентацию, чтобы каждая вершина соединялась с корнем (только одной) простой цепью.
Обратно, если Т= (X, В) - ориентированное дерево, то Т = (X, В), где В — множество дуг дерева Т без учета их ориентации, является неориентированным деревом.
«Генеалогическое дерево», в котором вершины соответствуют лицам мужского пола, а дуги ориентированы от родителей к детям, представляет собой хорошо известный пример ориентированного дерева. Корень в этом дереве соответствует «основателю» рода (лицу, родившемуся раньше остальных).
В настоящей главе приводится алгоритм порождения всех остовных деревьев произвольного неориентированного графа и даются методы прямого построения кратчайших остовных деревьев во взвешенном графе (в котором веса приписаны дугам). Кратчайшее остовное дерево (SST) графа находит, очевидно, применение при прокладке дорог (газопроводов, линий электропередач и т. д.), когда необходимо связать и точек некоторой сетью так, чтобы общая длина «линий связи» была минимальной. Если точки лежат на евклидовой плоскости, то их можно считать вершинами полного графа G с весами дуг, равными соответствующим «прямолинейным» расстояниям между концевыми точками дуг. Тогда, поскольку «разветвление» дорог допускается только в заданных п точках, SST графа G будет как раз требуемой сетью дорог, имеющей наименьший вес.
Если же «разветвление» дорог можно производить и «вне» заданных n точек, то возможна и более «короткая» (с меньшей стоимостью) сеть. Нахождение такой сети дорог представляет собой хорошо известную задачу Штейнера. Краткому обсуждению этой задачи посвящен последний раздел данной главы.






