Рассмотрим 2-элементное множество В, элементы которого 0 и 1. Однако они не являются числами в обычном смысле. Наиболее распространенная интерпретация двоичных переменных - это логическая. Например, в языках программирования вводится специальный тип переменной - логическая переменная, значения которой обозначаются TRUE и FALSE.
Таким образом, элементы множества В={0,1} будем рассматривать как формальные символы, а не числа.
Алгебра, образованная множеством В вместе со всеми возможными операциями на нем, называется алгеброй логики или булевой алгеброй.
Элементарные булевы функции
Определение 2.1. Булевой функцией f(x1, x2,..., xn) называется функция, которая принимает два значения 0 или 1 в зависимости от переменных хj, каждая из которых может также принимать только два значения 0 или 1.
Одной из важнейших интерпретаций теории булевых функций является теория переключательных функций. Первоначально математический аппарат теории булевых функций был применен для анализа и синтеза релейно-контактных схем с операциями последовательного и параллельного соединения контактов.
Любая булева функция может быть представлена таблицей, в левой части которой перечислены все наборы переменных, а в правой части - значения функции. Пример такого задания для трех переменных представлен в таблице.
Представление булевой функции
| x1 | x2 | x3 | f(х1,х2,х3) |
Для формирования столбца значений переменных удобен лексикографический порядок, в соответствии с которым каждый последующий набор значений получается из предыдущего прибавлением 1 в двоичной системе счисления, например, 100 = 011+ 1.
Булева функция п переменных может иметь 2n наборов. Поскольку функция принимает только два значения, общее число булевых функций и переменных равно 22n. Таким образом, функция одной переменой может иметь четыре значения: у = х; у = -x (отрицание х); у = 0 (константа 0); у = 1 (константа 1).
Из них выделим функцию "отрицание x" (обозначается -x ). Эта функция представлена в таблице
Функция отрицания
| x | -x |
Булевых функций двух переменных - 16. Те из них, которые имеют специальные названия, представлены в таблице.
Булевы функции двух переменных


Остальные функции специальных названий не имеют и могут быть выражены через перечисленные выше функции.
Формулы логики булевых функций
Формула логики булевых функций определяется индуктивно следующим образом:

Пример 2.1.

Часть формулы, которая сама является формулой, называется подформулой.
Пример 2.2.
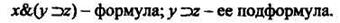
Функция/есть суперпозиция функций f1,f2,...,fn если f получается с помощью подстановок этих формул друг в друга и переименованием переменных.
Пример 2.3.
f1 = х1&х2 (конъюнкция); f2 -x (отрицание).
Возможны две суперпозиции:
1)f=f1(f2) = (—х1)&(—х2) - конъюнкция отрицаний;
2)f=f2(f1) = -(x1&х2) - отрицание конъюнкции.






