ЗАДАЧА
Дан неплоский четырехугольник. Доказать что два отрезка, каждый из которых соединяет середины противоположных сторон, и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся в ней пополам.
РЕШЕНИЕ
Пусть точки М, N, P, Q - середины сторон пространственного четырехугольника АВСД, а Е и F – середины его диагоналей. Обозначим О1, О2, О3 – середины отрезков М N, Р Q и Е F. Отрезки М N, Р Q и Е F пересекаются в одной точке и делятся в ней пополам тогда и только тогда, когда точки О1, О2, О3 совпадают.
Рассмотрим систему координат (А, АВ,АС,АД) и найдем координат вершин данного четырехугольника, середин его сторон и середин его диагоналей. А(0,0,0), В(1,0,0), С(0,1,0), Д(0,0,1), М(½, 0,0), Р(½,½,0),
N(0, ½,½), Q(0,0, ½), Е(0, ½,0), F(½,0, ½). Теперь найдем координаты точек О1, О2, О3. О1(¼, ¼, ¼), О2(¼, ¼, ¼), О3 (¼, ¼, ¼).
Так как точки О1, О2, О3 имеют одинаковые координаты в данной системе координат, то значит эти точки совпадают, т.е. середины отрезков М N, Р Q и Е F совпадают. ■
6.69. В неплоском шестиугольнике противоположные стороны попарно параллельны. Доказать, что а)противоположные стороны равны; б)диагонали, соединяющие противоположные вершины, пересекаются в одной точке и делятся в ней пополам.
6.70. Доказать, что в любом неплоском четырехугольнике середины всех сторон являются вершинами параллелограмма.
6.71.Точки М и Р являются серединами сторон АВ и СД пространственного четырехугольника АВСД. Доказать, что середины диагоналей двух четырехугольников АМРД и ВМРС являются вершинами параллелограмма или лежат на одной прямой.
6.72. В тетраэдре АВСД ребра АВ, АС, ДВ, ДС разделены точками M, N,
P, Q в одном и том же отношении λ. Доказать, что четырехугольник MNPQ является параллелограммом.
6.73. На сторонах АВ, ВС, СД, ДА пространственного четырехугольника АВСД выбраны точки А1, В1, С1, Д1 так, что А А1: А1В = ДС1: С1С = λ,
А Д1: Д1Д = ВВ1: В1С = μ. Доказать, что четырехугольник А1В1С1Д1 является плоским и точка, делящая диагональ А1С1 в отношении μ, совпадает с точкой, делящей диагональ В1 Д1 в отношении λ.
6.74. Дан тетраэдр АВСД и точка М на ребре АВ. Доказать, что середины отрезков АД, ВС, МД, МС лежит в одной плоскости.
6.75. Доказать, что в любом тетраэдре четыре отрезка, каждый из которых соединяет вершину тетраэдра с точкой пересечения медиан противоположной грани, пересекаются в одной точке и делятся в ней в отношении 3: 1, начиная от вершин.
ЗАДАЧА
Дан параллелепипед АВСД А1В1С1Д1. Точки М, Р, К являются серединами ребер СС1, АВ, С1Д1. Найти отношение объемов тетраэдров АВДА1 и Д1МРК.
РЕШЕНИЕ
Введем базис {А В, АД, АА1 }. Найдем координаты векторов Д1К, Д1М, Д1Р в этом базисе.
Д1К = Д1С1/ 2 = АВ / 2 
Д1К (½,0,0).
Д1М = Д1С1 + С1С / 2 = АВ – АА1 /2 Д1М (1, 0,- ½).
Д1Р = Д1Д + ДА + АВ / 2 = АВ /2 - АД - АА1 Д1Р (½, -1,-1)
Найдем объемы данных тетраэдров.
VАВДА1 = |А В АД АА1 |/ 6, VД1МРК = | Д1К Д1М Д1Р |/ 6,
Следовательно, VАВДА1: VД1МРК = |А В АД АА1 |: | Д1К Д1М Д1Р | (*)
Теперь выразим смешанное произведение векторов Д1К Д1М Д1Р, зная их координаты в базисе {А В, АД, АА1 }.
| ½ 0 0 |
Д1К Д1М Д1Р = | 1 0- ½ | (А В АД АА1) = - ¼ (А В АД АА1)
| ½ -1 -1 |
Из формул (*) и (**) получаем, что VАВДА1: VД1МРК = ¼.
ОТВЕТ. VАВДА1: VД1МРК = ¼.
6.76. Из вершины произвольного параллелепипеда проведены три диагонали прилежащих граней. Пользуясь свойствами смешанного произведения, выяснить, какую часть объема параллелепипеда составляет объем пирамиды, боковыми ребрами которой служат эти диагонали.
6.77. Точки А ', В', С ' делят ребра MА, МВ, МС тетраэдра МАВС в отношениях (МА, А') = λ1, (МВ, В') = λ2,(МС, С') = λ3. Найти отношение объемов тетраэдров МАВС и МА'В'С'.
6.78. Пирамида МАВСД, основанием которой является параллелограмм АВСД, пересечена плоскостью, проходящей через ребро АВ и середину ребра МС. Найти отношение объемов многогранников, на которые это плоскость делит данную пирамиду.
6.79. Объем правильной треугольной пирамиды с боковым ребром а равен а3/6. Найти плоский угол при вершине пирамиды.
6.80. Дан параллелепипед АВСД А1В1С1Д1. Найти отношение объемов этого параллелепипеда и тетраэдра АВ1СД1.
6.81. Дан параллелепипед АВСД А1В1С1Д1, Точки М, Р, К являются серединами ребер АА1, Д1С1, ВС. Найти отношение объемов тетраэдра
А1МРК и данного параллелепипеда.
6.82. Пользуясь векторным произведением, доказать, что площадь S треугольника АВС вычисляется по формуле S = ½ АВ АС sin А.
6.83. Все плоские углы при вершине О тетраэдра ОАВС прямые. Доказать, что квадрат площади грани АВС равен сумме квадратов площадей граней РАВ, ОВС, ОСА.
6.84. Найти площадь сечения прямоугольного параллелепипеда, длины ребер которого равны а, b, с, плоскостью, проходящей через середины трех ребер, выходящих из одной вершины.
ВОПРОСЫ К ГЛАВЕ 6
ОТВЕТЫ И УКАЗАНИЯ
6.4. а) А1(0,-3,4), А2(2,0,4), А3(2,-3,0); б) А1(0, 
,4), А2(-3,0,4), А3(-3, ,0).
6.5. АВ = ДС, ВС = АД, СД = ДЕ.
6.7. а) Д(6,5,7), Е(1,3,7); б) Д(-1,4,-3), Е(1, 3/2, -1).
6.8. В1(3,6,3), С1(7,7,3), Д1(8,3,0), С(5,4,4).
6.9. а) Да, б) нет, в) да, г) нет.
6.10. а) (2/3, 10/3, 7/3), б) (9/2, 0,0), в) (3, 5 + 2√2)/3, -3)
6.11. а) (-3, ½, 3), б) (17,6,-14), в) (-2,13,6).
6.12. С(4,-5,-2).
6.13. Пересекает ось Оz.
6.14. Да, (-3/2, 5/2, 11).
6.15. а) (7/4, ½, 11/12), б) (13/10, ½, 73/10).
6.17. Соs А = -89/91, Соs В = 23 
/ 77, Соs С = 36 / 143.
6.18. а) А1В1 = 5, В1В2 = 
, С1С2 = 
, б) ОМ = 5, ОN = 
,
ОР = 5, ОQ = 
.
6.19. 
.
6.22. 7, 
/2, 
/2.
6.23. (0,0,14/9).
6.24. (0,1,-2).
6.25. (1/2, 1, 3/2), r = 
/2.
6.28. 
, 
.
6.29. АМ =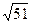 
/2, АН = 
.
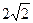6.30. Указание. По свойству биссектрисы АД Δ АВС ВД: ДС = АВ: АС.
6.31. а) Да, б) нет, в) да, г) нет.
6.32. а) Да, б) нет, в) нет, г) да.
6.34. а), б) и г) - левая, б) и д) – правая.
6.35. а), в) и г) – левая, б) и д) – правая.
6.36. базис правый.
6.37. а) х׳ = х – ½ у + 7z, у ׳ = ¼ у – ½ z, z ׳ = 2z;
б) х׳ = х + 2у - 5, у ׳ = х + у + 5, z ׳ = 1/5 z + 2/5;
в) х׳ = - х + 1, у ׳ = у – 1, z ׳ = - z + 2;
г) х׳ = х - 2, у ׳ = у – 5, z ׳ = z + 1;
д) х׳ = 5/8 х + 1/8 у + 3/8 z, у ׳ = ¾ х – ¼ у + ¼ z + 1,
z ׳ = 3/8 х – 1/8у – 3/8 z.
6.38. х = - ½ х׳ + ½ у׳ + ½ z׳ + ½, у = - ½ х׳ - ½ у׳ + ½ z׳ + ½,
z = - ½ х׳ - ½ у׳ - ½ z׳ + ½.
6.39. х׳ = - х – у – z + 1, у ׳ = у, z ׳ = z.
6.40. х = - ½ х׳ + ½, у = - ½ у׳ + ½, z = - ½ z׳ + ½.
6.41. а) х = х ׳ + 3, у = у ׳ – 4, z = z ׳ + 8
б) х = 4х ׳ – у ׳– z ׳, у = 3х ׳ + у ׳ – z ׳, z = - 6х ׳ - 5z ׳
6.42. а), б), в), д) - являются, г) – не являются.
6.43. М(а/2, а/2, а/2)
6.44. (11а, -9а, 5а/2)
6.45. а) -87, б) 204, в) 57, г) 0.
6.46. а) -29, б) 68, в) 19, г) 0,
6.47. а) 29, б) -3 .
6.48. р (-19, 0, -10), q (24, 54, 35).
6.49. α = 0, β = - 10, γ = - 20.
6.51. а) 50, б) 8, в) ½.
6.53. а) 2 [ а в ], б) 4[ в а ] + [ а с ] + 2[ с в ], в) 2[ а в ] + [ а с ], г) 0.
6.54. [ а в ] (-10,-8,19), | [ а в ] | = 
, [ в с ] (-1,2,-3), | [ в с ] | = ,
[ а с ] (-3, -1, 5), | [ а с ] | = 
.
6.55. а) (1,0,2), б) (10,5,-5), в) (-15,10,18), г) (-21, 13,14).
6.56. а) (-58, -20, 1), б) -80.
6.57. Указание. Найти координаты векторов, стоящих в правой и левой частях, в базисе { i, j, k }.
6.59. Указание. Умножив обе части данного равенства скалярно на вектор с, доказать, что a b с = 0.
6.60. Указание. Т.к.вектор р = [ АВ АС ] 
(АВС), то доказать, что данный вектор перпендикулярен вектору р.
6.61. Указание. а) выразисть с = - а – b и найти [ b с ] и [ с а ].
б) От любой точки О отложить векторы ОА = а, ОВ = b, ОС = с. Доказать, что векторы [а b ], [ b с ], [ с а ] перпендикулярны одной плоскости γ, содержищей точки О, А, В, С.
6.62. Указание. Если а 
0, то ввести такой базис { i, j, k }, у которого
