РЕШЕНИЕ
Обозначим [СВ СС1] = р. Тогда по определению векторного произведения имеем
1, Длина вектора р равна площади параллелограмма, построенного на векторах СВ и СС1,но этот параллелограмм является квадратом с единичной стороной, поэтому │р│= 1.
2. р 
СВ, р СС1, следовательно вектор р коллинеарен вектору СД.
3. Базис { СВ, СС1 р} правый. Но по условию базис
{АВ, АД, АА1 } – правый, этот базис соответствует левой руке, следовательно базис { СВ, СС1 р} также соответствует левой руке.
Из 2. и 3. следует, что вектор р = СР = - СД.
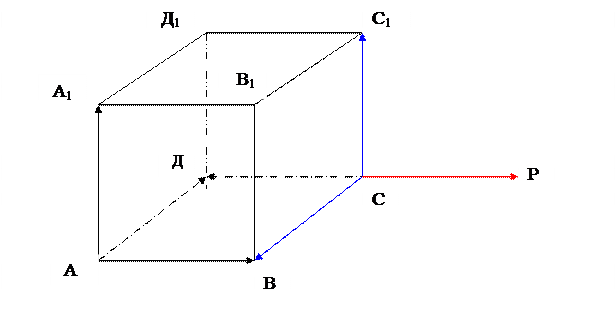
6.52. Дан прямоугольный параллелепипед АВСД А1В1С1Д1, │АВ│= 2, │АД│= 1, │АА1│= ½. Базис {ВА, ВС ВВ1 } – левый. Построить вектор, равный векторному произведению векторов
а) СД и СС1, б) Д1А1 и ДС, в) В1С1 и ВВ1.
ЗАДАЧА
Найти [( 3 а + 2 b) ( 5 а – 3 b)], если [а b] = с.
РЕШЕНИЕ
Используя свойства векторного произведения, упростим данное векторное произведение.
[( 3 а + 2 b) ( 5 а – 3 b)] = [ 3 а ( 5 а + 3 b)] + [ 2 b ( 5 а -3 b)] = [ 3 а 5 а] + [ 3 а 3 b] +
[ 2 b 5 а ] + [ 2 b(- 3 b)] = 0 + 9 [а b] + 10 [b а ] - 0 = 9 [а b] -10 [а b] =
- [а b] = -с
ОТВЕТ - с.
6.53. Упростить выражения: а) [(а – b) (а + b)], б) [(а + 2 b - с) (а -2 b)],
в) [а ( 2 b + с – 3 а)], г) [(а – р) (а - р)].
ЗАДАЧА
В ортонормированном правом базисе даны векторы а (5,1,0),
B(2,2,-1), с(1,-3,1), d(0,0,1). Найти координаты вектора [ [а b ] [с d ]].
РЕШЕНИЕ
1. Сначала найдем координаты векторных произведений [а b ] и [с d ].
| i j k|
[а b ] = | 5 1 0 | = - i + 5 j + 8 k 
[а b ] (- 1, 5, 8 ).
| 2 2 -1 |
| i j k|
[с d ] = | 1 -3 1 | = -3 i -1 j + 0 k [с d ] (- 3, -1, 0 ).
| 0 0 1 |
2. Теперь найдем координаты [ [а b ] [с d ]].
| i j k |
[[а b ] [с d ]] = | -1 5 8 | = 5 i -24 j + 16 k [[а b ] [с d ]] ( 5,-24,16).
|- 3 -1 0 |
ОТВЕТ. (5, -24, 16).
6.54. В ортонормированном правом базисе даны векторы а (3,1,2),
b (2,7,4), с (1,2,1). Найти координаты векторов [а b ], [ b с ], [а с ] иих длины.
6.55. В ортонормированном правом базисе даны векторы а (0,1,0),
b (2,-1,3), с (0,5,-2), d (1,2,-3). Найти координаты векторов:
а) [а (b + с) ]; б) [b (d - с) ]; в) [(с -2 d) (с + b) ]; г) [(а+ b)(с + d)].
6.56. В ортонормированном правом базисе даны векторы а (3,0,-1),
b (2,4,3), с (-1,3,2), d (2,0,1). Найти а) координаты вектора [ [а b ] с],
б) скалярное произведение [а с ] · [ b d ].
6.57. Дан ортонормированный базис { i, j, k }. Доказать, что для любых векторов а и b [а b ] = (а b i) i +(а b j) j + (а b k) k.
6.58. Доказать, что для любых векторов а, b и с верно, что:
а) [(а – b)(а + b)] = 2 [а b], б) [ (b – а)(с – b)] = [а b] + [ bс] + [с а].
6.59. Доказать, что если [а b] + [b с] + [с а] = 0, то векторы а, b, с
компланарны.
6.60. Векторы ОА = а, ОВ = b, ОС = с не компланарны. Доказать, что вектор [а b] + [b с] + [с а] перпендикулярен плоскости(АВС).
6.61. Доказать, что а) если а + b + с = 0, то [а b] = [b с] = [с а],
б) если векторы а и b не коллинеарны и [а b] = [b с] = [с а], то
а + b + с = 0.
6.62. Доказать тождества: а) [а b]2 + (а b)2 = а2 b2,
б) [ [а b] с] = b(ас) – а(bс).
ЗАМЕЧАНИЕ. В задачах 63) – 68) система координат прямоугольная декартовая.
ЗАДАЧА
Дана треугольная призма АВСА1В1С1 с основанием АВС. Найти длину ее высоты АН если А(1,0,1), В(5,0,0), С(0,1,2), А1(3,-1,1).
РЕШЕНИЕ
Объем призмы равен произведению площади основания на высоту, т.е
VАВСА1В1С1 = SАВС АН. (*)
Найдем координаты АВ, АС, АА1 . АВ (4,0,-1), АС (-1,1,1), АА1 (2,-1,0).
Найдем объем призмы. VАВСА1В1С1 = ½ | АВ АС АА1 |.
| 4 0 -1 |
АВ АС АА1= | -1 1 1 | = 5 VАВСА1В1С1 = 5/2
| 2 -1 0 |
Найдем площадь основания. SАВС = | [АВ АС ] | / 2.
| i j k |
[АВ АС ] = | 4 0 -1 | = i -5 j + 4 k [АВ АС ] ( 1, -5, 4 )
| -1 1 1 |
| [АВ АС ] | =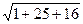 
= 
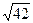
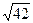SАВС = / 2.
Из формулы (*) следует, что АН =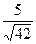 
.
ОТВЕТ. АН = .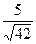
6.63. Найти площадь треугольника АВС, если а) А(3,4,-1), В(2,0,3),
С(-3,5,4), б) А(-1,1,2), В(1,1,0), С(2,6,-2).
6.64. Найти длину высоты АН тетраэдра АВСД, если А(2,-4,5), В(-1,-3,4), С(5,5,-1), Д(1,-2,2).
6. 65. Дан параллелепипед АВСД А1В1С1Д1, построенный на векторах
АВ (4,3,0), АД (2,1,2), АА1 (-3,-2,5). Найти а)объем параллелепипеда; б)площади граней, в) высоту, проведенную из вершины А1 на грань АВСД;
г) косинус угла между ребром АВ и диагональюВ1Д; д) косинус угла между гранями АВСД и АДД1А1.
6.66. Дана треугольная призма АВСА1В1С1 с основанием АВС, построенная на векторах АВ (0,1,-1), АС (2,-1,4), АА1 (-3,2,2). Найти а)объем призмы;
б) площади граней; в) высоту призмы; г) угол между ребрами В1С1 и АА1.
6.67. Дан тетраэдр АВСД, построенный на векторах АВ (2,0,0), АС (3,4,0), АД (3,4,2). Найти а)объем тетраэдра; б) площади граней; в)высоту ДН;
г) косинус угла между ребрами АВ и ВС; д) угол между гранями АВС и АДС.
6.68. Доказать, что четырехугольник АВСД, где А(2,-3,1), В(-1,1,1), С(-4,5,6), Д(2,-3,6), является плоским и найти его площадь.
