Розглядаємо два ненульових полінома 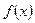 та
та  степенів
степенів 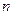 та
та  відповідно, нехай
відповідно, нехай 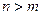 .
.
1. Ділимо 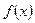 на
на  .
.
Якщо  , то
, то
 - НСД знайдено,
- НСД знайдено,
інакше
 .
.
В останньому випадку з властивості 4 подільності поліномів спільний дільник поліномів 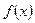 та
та  є також дільником остачі
є також дільником остачі 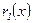 . Тобто НСД між
. Тобто НСД між 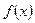 та
та  співпадає з НСД між
співпадає з НСД між  та
та 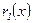 . Можна зробити перехід до розшуку НСД між
. Можна зробити перехід до розшуку НСД між  та
та 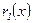 . При цьому степінь поліномів зменшується.
. При цьому степінь поліномів зменшується.
2. Ділимо  на
на 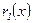 .
.
Якщо  , то
, то
 - НСД знайдено,
- НСД знайдено,
інакше
 .
.
Переходимо до розшуку НСД між 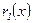 та
та  . При цьому степінь поліномів знову зменшується.
. При цьому степінь поліномів знову зменшується.
3.  .
.
………………….
k-1.  .
.
k.  .
.
k+1. 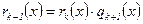 .
.
Оскільки степінь поліномів  на кожному кроці зменшується, то процес поетапного ділення завжди буде скінченим, граничним значення остач буде поліном 0-го степеня.
на кожному кроці зменшується, то процес поетапного ділення завжди буде скінченим, граничним значення остач буде поліном 0-го степеня.
З останнього кроку видно, що  .
.
Простежуючи поступово вгору ланцюжок ділень, можна зробити висновок, що 
Отже, можна зробити висновок, що в алгоритмі Евкліда НСД між поліномами 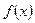 та
та  буде дорівнювати останній ненульовій остачі
буде дорівнювати останній ненульовій остачі  з ланцюжка поступових ділень.
з ланцюжка поступових ділень.
Якщо НСД між поліномами 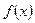 та
та  є поліном 0-го степеня - число
є поліном 0-го степеня - число  , то з урахуванням властивості 5 подільності поліномів можна стверджувати, що в такому випадку НСД між
, то з урахуванням властивості 5 подільності поліномів можна стверджувати, що в такому випадку НСД між 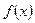 та
та  дорівнює 1.
дорівнює 1.
Застосувавши властивість 5 подільності поліномів, до  - полінома степеня, більшого за 0, можна
- полінома степеня, більшого за 0, можна  подати таким чином:
подати таким чином:

Скоротивши НСД на 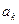 згідно властивості подільності поліномів 5, отримаємо, що
згідно властивості подільності поліномів 5, отримаємо, що 
Висновки:
1. Алгоритм Евкліда є завжди скінченим.
2. За алгоритмом Евкліда знаходимо НСД двох поліномів з точністю до числа.
3.  , де
, де 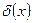 - поліном з коефіцієнтом біля старшого степеня
- поліном з коефіцієнтом біля старшого степеня  .
.
4. Два полінома взаємно прості тоді і тільки тоді, коли  .
.
Приклад 1
За алгоритмом Евкліда найти НСД між  та
та 
Розв’язання.
1. Ділимо 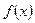 на
на  .
.

| 
| 
| 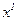
| 
| 
| 
| 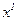
| 
| |
| × 3 | -1 | -4 | -3 | -3 | |||||
| _ 3 | -3 | -12 | -9 | -1 | |||||
| -3 | |||||||||
| × 3 | -1 | -5 | -9 | -9 | |||||
| _-3 | -15 | -27 | -27 | ||||||
| -3 | -10 | -2 | |||||||
| : (-5) | -5 | -25 | -30 | ||||||
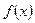 можна подати так:
можна подати так:
 , тобто
, тобто
 , степінь остачі менша за степінь
, степінь остачі менша за степінь 

Оскільки нас цікавить НСД з точністю до числа, то ми можемо в процесі ділення множити поліном, що ділиться, на число а залишок скоротити на спільний для всіх його коефіцієнтів дільник.
Отже, за 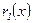 можна взяти
можна взяти 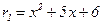
2. Ділимо  на
на 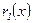 .
.

| 
| 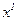
| 
| 
| 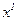
| 
| |
| _ 3 | -3 | ||||||
| -5 | |||||||
| _-5 | -16 | -3 | |||||
| -5 | -25 | -30 | |||||
| : 9 | |||||||
 можна подати так:
можна подати так:
 , тобто
, тобто
 , степінь остачі менша за степінь
, степінь остачі менша за степінь 

3. Ділимо 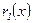 на
на  .
.

| 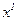
| 
| 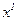
| 
|
| _ 1 | ||||
| _ 2 | ||||
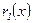 можна подати так:
можна подати так:
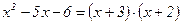 , тобто
, тобто
 .
.
Процес поступового ділення можна зупинити. Останній ненульовий залишок ланцюжка ділень є 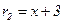 .
.
Отже, за алгоритмом Евкліда НСД між  та
та  дорівнює
дорівнює  .
.
Відповідь.







