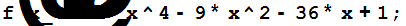В системе Mathematica реализованы алгоритмы разложения многочлена на множители над различными числовыми полями.
Пусть 
поле рациональных чисел, 
многочлен с коэффициентами из этого поля. Разложение осуществляется при выполнении команды Factor[f[x]]
Пример 3.3.2. Разложить на неприводимые множители над полем рациональных чисел следующий многочлен
Решение.
Factor[f[x]]
Рассмотрим множество комплексных чисел следующего вида
,
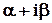где 
и 
рациональные числа, 
. Можно проверить, что это множество образует числовое поле. Это поле называется полем гауссовых чисел. Разложение многочлена на множители, неприводимые над этим полем реализуется следующим образом.
Пример 3.3.3. Разложить на неприводимые множители над полем гауссовых чисел многочлен 
.
Решение.
Рассмотрим множество чисел вида 
, где и - гауссовы числа. Легко проверить, что это множество чисел так же образует числовое поле. Разложение многочлена на множители с коэффициентами из указанного поля производится следующим образом
Пример 3.3.4.Разложить на множители над рассматриваемым полем многочлен 
.
Решение.
В системе Mathematica можно производить разложение многочлена на неприводимые множители над полем, которое не является числовым.
Пример 3.3.5. Разложить на неприводимые множители над полем классов вычетов по модулю 2 многочлен 
.
Решение.
2.4 Корни многочлена.
Если при значении 
многочлен принимает значение 
, то число 
называется корнем этого многочлена. Всякий многочлен ненулевой степени с любыми числовыми коэффициентами имеет хотя бы один корень, действительный или комплексный.
Известно, что корни любого многочлена, степень которого не превосходит четырёх, выражаются через его коэффициенты при помощи операций сложения, вычитания, умножения, деления и извлечения корня. Пользуясь системой Mathematica, мы можем находить все корни указанных многочленов вне зависимости от того, являются ли коэффициенты рассматриваемых многочленов числами или символьными величинами.
Пример 3.4.1. Найти корни многочлена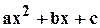 
.
Решение.
Мы видим, что, выполняя указанную команду, система не только находит корни многочлена, но и производит исследование их числа в зависимости от значений коэффициентов.
Пример 3.4.2. Найти корни многочлена 
.
Решение.
Если коэффициенты многочлена не содержат параметров, то система Marhematica позволяет найти приближённые значения корней этого многочлена.
Пример 2.4.3. Найти приближённые значения корней многочлена
.
Решение.
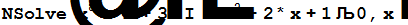
{{x®-1.18858+0.532643 ä},{x®-1.05423-0.786636 ä},
{x®-0.23021-0.286179 ä},{x®-0.0726108+1.28631 ä},
{x®-0.06423+0.46295 ä},{x®0.176451 -1.35633 ä},
{x®1.15738 +0.73759 ä},{x®1.27604 -0.590341 ä}}
Если коэффициенты многочлена, степень которого больше четырёх, содержат параметр, то система Mathematica позволяет графически изобразить зависимость вещественных корней уравнения от этого параметра.
Пример 4.4. 2. Изобразить графически зависимость корня многочлена
от параметра 
.
Решение.
y=x/.R[[1]];
Plot[y,{a,-2,2},PlotStyle->{Thickness[0.01]}]
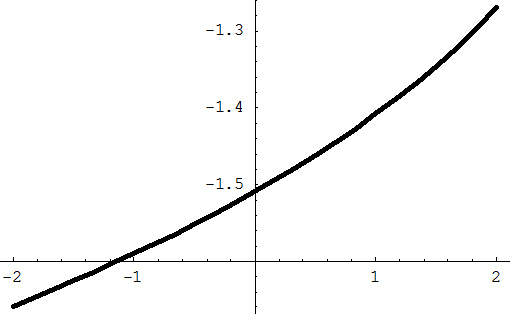
Пусть 
- многочлен с действительными коэффициентами. Число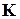 
называется верхней границей вещественных корней многочлена , если этот многочлен не имеет вещественных корней, больших или равных 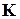. Аналогично определяется верхняя и нижняя границы положительных или отрицательных корней многочлена.
Если 
верхняя граница положительных корней многочлена , а 
- верхняя граница положительных корней многочлена 
то вещественные корни многочлена расположены в промежутке 
.
Пусть - многочлен степени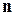 
с вещественными коэффициентами. Можно доказать, что если при многочлен и его производные 
положительны, то является верхней границей положительных корней рассматриваемого многочлена. Система Mathematica позволяет найти промежуток, на котором многочлен и все его производные положительны и, тем самым найти верхнюю границу положительных корней многочлена. Аналогично находится и нижняя граница его корней.
Мы можем построить график многочлена на полученном промежутке, а затем, используя специальные функции для вычисления нулей многочлена, получить их значение с нужной точностью.
Пример 3.4.4. Найти промежуток, на котором расположены вещественные корни многочлена 
и получить их значения с точностью до восьми десятичных знаков.
Решение.
