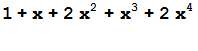X=T.Y
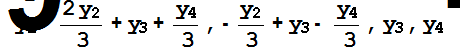
Находим канонический вид данной квадратичной формы
Expand[X.A.X]

Опишем ещё один способ приведения квадратичной формы к каноническому виду, который эффективно реализуется в системе Mathematica.
1. Строим матрицу из собственных векторов матрицы данной квадратичной формы.
2. Нормируем строки этой матрицы.
3. Находим для полученной матрицы транспонированную матрицу. Эта матрица и будет задавать невырожденное линейное преобразование переменных исходной квадратичной формы, приводящее её к каноническому виду.
Рассмотрим следующий
Пример. Привести к каноническому виду следующую квадратичную форму
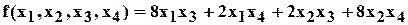
Решение.
Вводим матрицу квадратичной формы

Находим собственные векторы матрицы A и нормируем их
H=Eigenvectors[A]
{{-1,-1,1,1},{1,1,1,1},{1,-1,-1,1},{-1,1,-1,1}}
Do[H[[i]]=H[[i]]/Norm[H[[i]]],{i,1,4}];
Находим невырожденное преобразование переменных, приводящее квадратичную форму к каноническому виду
T=Transpose[H];


X=H.Y
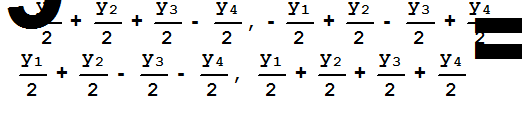
Находим канонический вид данной квадратичной формы
g=Expand[X.A.X]
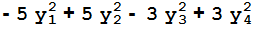
Находим собственные числа матрицы квадратичной формы.
Eigenvalues[A]
{-5,5,-3,3}
Мы видим, что при данном способе приведения квадратичной формы к каноническому виду, коэффициенты полученной квадратичной формы совпадают с собственными числами матрицы A.
Алгебра многочленов
Задание многочлена. Действия с многочленами в системе Mathematica
Как известно, многочленом от переменной  называется выражение
называется выражение
вида
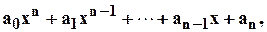
где  натуральное число,
натуральное число, 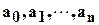 - элементы некоторого числового поля, называемые коэффициентами этого многочлена. Выражения
- элементы некоторого числового поля, называемые коэффициентами этого многочлена. Выражения 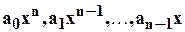 называются членами многочлена,
называются членами многочлена, 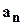 - свободным членом.
- свободным членом.
Многочлен называется нулевым, если все его коэффициенты равны нулю.
Если 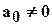 , то
, то 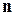 называют степенью многочлена, а
называют степенью многочлена, а 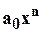 - старшим членом многочлена.
- старшим членом многочлена.
В системе Mathematica многочлен можно задавать, например, таким способом

Вычислить значение этого многочлена при конкретном значении переменной  можно так
можно так
f[11]
Если мы хотим определить произвольный многочлен четвёртой степени, не указывая конкретных значений коэффициентов, то это можно сделать так
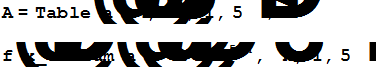

Многочлены можно складывать, вычитать и умножать по обычным правилам раскрытия скобок и приведения подобных членов. Продемонстрируем выполнение указанных действий над многочленами в системе Mathematica.


Система Mathematica позволяет производить указанные действия над многочленами при условии, что их коэффициенты принадлежат тому или иному классу вычетов по заданному модулю. Рассмотрим, например, вычисление произведения двух многочленов в поле классов вычетов по модулю 2.
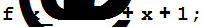
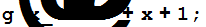
Expand[f[x]*g[x],Modulus®2]
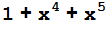
Пусть  и
и 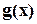 - два многочлена и многочлен
- два многочлена и многочлен 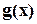 не является нулевым. Тогда можно всегда подобрать такую пару многочленов
не является нулевым. Тогда можно всегда подобрать такую пару многочленов 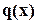 и
и 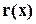 , частное и остаток, что
, частное и остаток, что
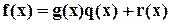 ,
,
причём 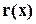 или нулевой многочлен или многочлен, степень которого меньше степени многочлена
или нулевой многочлен или многочлен, степень которого меньше степени многочлена 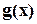 . Если многочлен
. Если многочлен 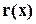 является нулевым, то говорят, что многочлен
является нулевым, то говорят, что многочлен  делится на многочлен
делится на многочлен 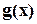 .
.
В системе Mathematica частное от деления многочлена  на
на 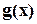 и остаток находятся следующим образом
и остаток находятся следующим образом
f[x_]=
g[x_]=
q[x_]=PolynomialQuotient[f[x],g[x],x]
r[x_]=PolynomialRemainder[f[x],g[x],x]
Рассмотрим следующие примеры
Пример 2.1. Разделить с остатком многочлен 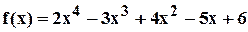 на многочлен
на многочлен 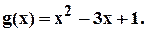
Решение.

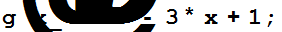
r[x_]=PolynomialRemainder[f[x],g[x],x]
-5+25 x
q[x_]=PolynomialQuotient[f[x],g[x],x]

Пример 2.2. Найти частное и остаток от деления многочлена  на многочлен
на многочлен 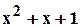 над полем классов вычетов по модулю 3.
над полем классов вычетов по модулю 3.
Решение.
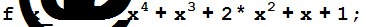
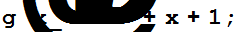
r[x_]=PolynomialMod[
PolynomialRemainder[f[x],g[x],x],Modulus®3]
x
q[x_]=PolynomialMod[
PolynomialQuotient[f[x],g[x],x],Modulus®3]
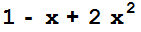
Производим проверку
Expand[g[x]*q[x]+r[x],Modulus®3]