Система линейных уравнений имеет вид
 (3.1)
(3.1)
Здесь 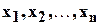 - неизвестные,
- неизвестные,  - коэффициенты при неизвестных,
- коэффициенты при неизвестных,  свободные члены.
свободные члены.
Решением системы уравнений (3.1) называется упорядоченный чисел
 (3.2)
(3.2)
удовлетворяющий всем уравнениям данной системы, т.е. при замене неизвестных на соответствующие числа все уравнения обращаются в верные равенства. Числа (3.2) называются значениями неизвестных 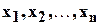 в данном решении.
в данном решении.
Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система называется определённой, если она имеет единственное решение, и неопределённой, если более одного решения. Неопределённая система всегда имеет бесконечное множество решений.
Две системы линейных уравнений называются эквивалентными, если каждое решение первой системы является решением второй, и обратно.
Элементарными преобразованиями системы линейных уравнений называются преобразования следующих трёх типов:
1) перестановка двух уравнений;
2) умножение обеих частей одного из уравнений на любое отличное от нуля число;
3) прибавление обеих частей одного уравнения соответствующих частей другого, умноженных на любое число.
Элементарные преобразования переводят данную систему уравнений в эквивалентную систему.
Матрицей системы уравнений (3.1) называется матрица из коэффициентов при неизвестных
 (3.2)
(3.2)
Расширенной матрицей называется матрица, полученная из матрицы системы добавлением столбца свободных членов, т.е. матрица
 (3.3)
(3.3)
Отметим, что каждому элементарному преобразованию строк расширенной матрицы системы однозначно соответствует элементарное преобразование самой системы.
Вопрос о совместности системы (3.1) решает следующий критерий Кронекера- Капели: для того, чтобы система линейных уравнений (3.1) была совместна необходимо и достаточно, чтобы ранг матрицы  системы был равен рангу расширенной матрицы
системы был равен рангу расширенной матрицы  .
.
Рассмотрим следующий пример. Имеется система линейных уравнений
Исследовать на совместность следующую систему линейных уравнений

Составляем матрицу системы

Составляем расширенную матрицу

MatrixRank[A]
MatrixRank[B]
Так как ранги матрицы системы и расширенной матрицы равны, то система совместна.
Перейдём к рассмотрению способов решения систем линейных уравнений.
Предположим сначала, что число уравнений системы равно числу неизвестных и равно рангу матрицы системы.
1. Метод элементарных преобразований.
При использовании этого метода расширенная матрица системы приводится одним из рассмотренных ранее способов к ступенчатому виду. Отметим, что при выборе главного элемента столбец свободных членов не рассматривается.Рассмотрим следующий пример.
Решить систему
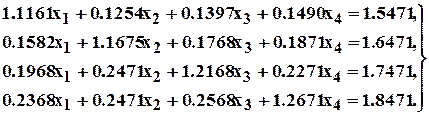
Записываем матрицу системы и расширенную матрицу.

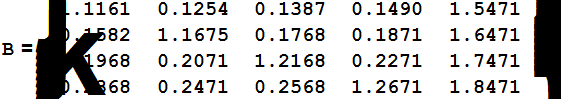
Находим ранги этих матриц
MatrixRank[A]
MatrixRank[B]
Система совместна. Приводим матрицу B к ступенчатому виду.
MatrixForm[RowReduce[B]]

Отсюда видно

2. Метод обратной матрицы.
При решении системы линейных уравнений этим методом находим матрицу, обратную для матрицы системы, затем столбец из свободных членов умножаем на эту матрицу. Решим этим способом систему линейных уравнений, рассмотренную в предыдущем примере.
Записываем матрицу системы и вектор из свободных членов

B={1.5471,1.6471,1.7471,1.8471};
Находим вектор из решений рассматриваемой системы.
X=Inverse[A].B
{1.04058,0.986956,0.935053,0.881297}
3. Метод Крамера.
Для решения системы линейных уравнений методом Крамера в системе Mathematica поступаем следующим образом.
1) Находим матрицу  , транспонированную к матрице
, транспонированную к матрице  .
.
2) Для нахождения неизвестной 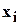 в матрице
в матрице  строку с номером
строку с номером  заменяем вектором свободных членов, и определитель полученной матрицы делим на определитель матрицы
заменяем вектором свободных членов, и определитель полученной матрицы делим на определитель матрицы  .
.
Продемонстрируем этот метод на том же примере.
Записываем матрицу системы и вектор из свободных членов

B={1.5471,1.6471,1.7471,1.8471};
Находим матрицу, транспонированную к матрице A.
A1=Transpose[A];
Находим решение системы линейных уравнений.

1.04058

0.986956
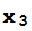
0.935053

0.881297
4. Решение системными средствами.
Mathematica содержит специальную функцию для решения систем линейных уравнений. При этом она позволяет решать задачи большой размерности за сравнительно короткое время.
Задаём матрицу системы.
A=Table[Random[],{i,1,1000},{j,1,1000}];
Do[A[[i,i]]=2,{i,1,1000}];
Задаём вектор свободных членов.
B=Table[35*Sin[i*0.01],{i,1,1000}];
Решаем систему и измеряем время решения.
X=Timing[LinearSolve[A,B]]
X[[1]]
0.578 Second
Оцениваем точность решения.
Max[Abs[A.X[[2]]-B]]

Рассмотрим теперь решение систем однородных уравнений.
Линейное уравнение называется однородным, если его свободный член равен нулю. Система линейных однородных уравнений имеет вид
 (3.3)
(3.3)
Всякая система линейных однородных уравнений имеет нулевое решение  и, следовательно, совместна. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы ранг
и, следовательно, совместна. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы ранг  этой системы (т.е. ранг матрицы из коэффициентов при неизвестных) был меньше числа неизвестных
этой системы (т.е. ранг матрицы из коэффициентов при неизвестных) был меньше числа неизвестных 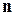 . Отсюда следует, в частности, что любая система однородных уравнений, в которой число уравнений меньше числа неизвестных, имеет ненулевое решение.
. Отсюда следует, в частности, что любая система однородных уравнений, в которой число уравнений меньше числа неизвестных, имеет ненулевое решение.
Для того чтобы система однородных линейных уравнений, в которой число уравнений равно числу неизвестных, имела ненулевое решение необходимо и достаточно, чтобы определитель матрицы этой системы был равен нулю.
Любое решение

системы линейных уравнений с 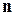 неизвестными можно рассматривать как вектор
неизвестными можно рассматривать как вектор  . Поэтому имеют смысл такие понятия, как сумма двух решений, произведения решения на число, линейная комбинация решений или линейная независимость решений. Отметим следующие свойства решений системы линейных однородных уравнений.
. Поэтому имеют смысл такие понятия, как сумма двух решений, произведения решения на число, линейная комбинация решений или линейная независимость решений. Отметим следующие свойства решений системы линейных однородных уравнений.
1) Сумма двух решений есть решение.
2) Произведение решения на любое число есть решение.
3) Линейная комбинация решений есть решение.
Фундаментальной (или основной) системой решений для системы однородных уравнений (2.2) называется линейно независимая система решений, через которую линейно выражается любое решение этой системы.
Если ранг системы уравнений (2.2)  равен числу неизвестных, то эта система не имеет фундаментальной системы решений, так как её единственным решением будет нулевое решение, составляющее линейно зависимую систему. Если
равен числу неизвестных, то эта система не имеет фундаментальной системы решений, так как её единственным решением будет нулевое решение, составляющее линейно зависимую систему. Если  , то система
, то система  имеет бесконечно много фундаментальных систем, причём каждая из них состоит из
имеет бесконечно много фундаментальных систем, причём каждая из них состоит из  решений. Общее решение системы (2.2) является линейной комбинацией решений, входящих в фундаментальную систему.
решений. Общее решение системы (2.2) является линейной комбинацией решений, входящих в фундаментальную систему.
Mathematica позволяет для данной однородной системы линейных уравнений найти её фундаментальную систему решений и, следовательно, найти общее решение.
Рассмотрим следующий пример. Найти фундаментальную систему решений и общее решение системы

Записываем матрицу системы и вычисляем её ранг

MatrixRank[A]
Фундаментальная система состоит из 4-2=2 линейно независимых решений. Находим одну из таких систем.
R=NullSpace[A]
{{-7,5,0,1},{8,-6,1,0}}
Находим общее решение данной системы.
m=Length[R]
C1=Table[c[i],{i,1,m}];
X=C1.R
{-7 c[1]+8 c[2],5 c[1]-6 c[2],c[2],c[1]}
Предположим теперь, что нам дана неоднородная система уравнений, у которой ранг матрицы системы меньше числа неизвестных. Такая система имеет бесконечно много различных решений. Для построения общего решения этой системы поступаем следующим образом.
1) Находим одно из решений данной системы.
2) Находим общее решение соответствующей однородной системы.
Сумма указанных решений и даст общее решение рассматриваемой системы уравнений.
Пусть, например, нам требуется найти общее решение следующей системы уравнений
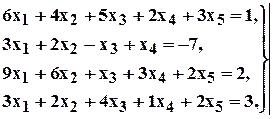
Водим матрицу системы

Находим ранг этой матрицы
MatrixRank[A]
Строим расширенную матрицу

Находим ранг этой матрицы
MatrixRank[B]
Так как ранг матрицы системы равен рангу расширенной матрицы, то система совместна. Находим одно из решений этой системы.
C1={1,-7,2,3};
X1=LinearSolve[A,C1]
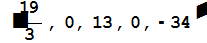
Находим общее решение соответствующей однородной системы.
R=NullSpace[A]
{{-1,0,0,3,0},{-2,3,0,0,0}}
m=Length[R]
C1=Table[c[n],{n,1,m}];
X=X1+C1.R
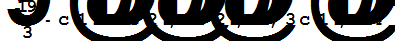
Пусть {  } - система векторов, из которых по крайней мере один отличен от нуля. Линейной оболочкой векторов этой системы называется множество векторов следующего вида
} - система векторов, из которых по крайней мере один отличен от нуля. Линейной оболочкой векторов этой системы называется множество векторов следующего вида

Линейная оболочка системы векторов {  } образует линейное подпространство исходного пространства. Пусть
} образует линейное подпространство исходного пространства. Пусть  произвольный вектор. Представим его в виде суммы
произвольный вектор. Представим его в виде суммы

где вектор 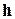 ортогонален каждому из векторов
ортогонален каждому из векторов  ,а вектор
,а вектор  является линейной комбинацией этих векторов.. Вектор
является линейной комбинацией этих векторов.. Вектор 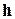 называется перпендикуляром, опущенным из вектора
называется перпендикуляром, опущенным из вектора  на линейную оболочку векторов рассматриваемой системы, а вектор
на линейную оболочку векторов рассматриваемой системы, а вектор  - проекцией вектора
- проекцией вектора  на эту оболочку.
на эту оболочку.
Пусть  проекция вектора
проекция вектора  на линейную оболочку векторов
на линейную оболочку векторов  . Тогда
. Тогда
 .
.
Найдём коэффициенты этой линейной комбинации. Так как вектор  ортогонален каждому из векторов
ортогонален каждому из векторов  , то выполняются соотношения
, то выполняются соотношения

Отсюда следует, что коэффициенты  можно определить из следующей системы линейных уравнений
можно определить из следующей системы линейных уравнений

После этого легко находятся векторы  и
и 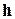 .
.
Рассмотрим следующий пример.
Даны векторы

и вектор  . Найти проекцию вектора
. Найти проекцию вектора  на линейную оболочку векторов
на линейную оболочку векторов  и перпендикуляр
и перпендикуляр 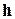 из вектора
из вектора  на эту оболочку.
на эту оболочку.
Находим проекцию вектора  на линейную оболочку заданных векторов.
на линейную оболочку заданных векторов.

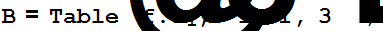
R=LinearSolve[A,B];








