PolynomialGCD[f[x],g[x],h[x]]
-1+x
Если  - наибольший общий делитель многочленов
- наибольший общий делитель многочленов  и
и 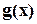 , то всегда можно подобрать два таких новых многочлена
, то всегда можно подобрать два таких новых многочлена 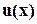 и
и 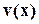 , что
, что
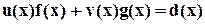 . (2.1)
. (2.1)
Равенство (2.1) называют линейным представлением наибольшего общего делителя.
Многочлены 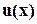 и
и 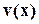 можно подобрать таким образом, что степень многочлена
можно подобрать таким образом, что степень многочлена 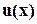 будет не больше степени многочлена
будет не больше степени многочлена 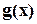 , а степень многочлена
, а степень многочлена 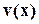 - не больше степени многочлена
- не больше степени многочлена  . Сделать это можно, например, методом неопределённых коэффициентов.
. Сделать это можно, например, методом неопределённых коэффициентов.
Пример 3.3. Найти линейное представление наибольшего общего делителя следующих многочленов

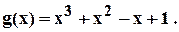
Решение.

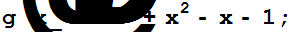
Находим наибольший общий делитель заданных полиномов
d[x_]=PolynomialGCD[f[x],g[x]]
1+x
Так как g[x]- многочлен третьей степени, то u[x] будем искать в виде многочлена второй степени; так как f[x] многочлен четвёртой степени, то многочлен v[x] будем искать в виде многочлена третьей степени.
A=Table[a[n-1],{n,1,7}];
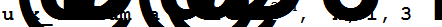

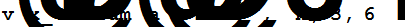

d1[x_]=f[x]*u[x]+g[x]*v[x];
T1=Table[Coefficient[d1[x],x,n-1],{n,1,7}];
T2=Table[Coefficient[d[x],x,n-1],{n,1,7}];
T=Table[T1[[n]]ŠT2[[n]],{n,1,7}];
R=Solve[T,A]
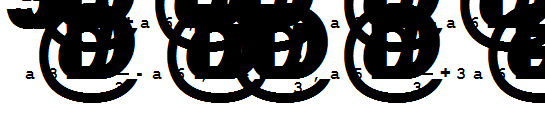
a[6]=0;
u[x_]=u[x]/.R[[1]]
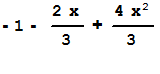
v[x_]=v[x]/.R[[1]]
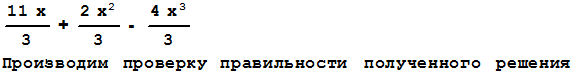
Expand[f[x]*u[x]+g[x]*v[x]]
X
Та же задача может быть решена другим способом. Положим 
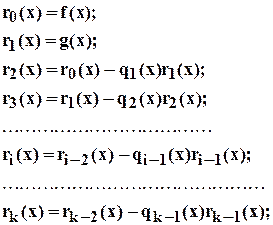
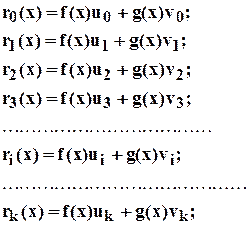
В левом столбце- последовательность делений, которая разрешена относительно остатков. В правом столбце каждый остаток выражен в виде 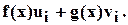 Мы хотим вычислить
Мы хотим вычислить  и
и 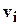 . Очевидно, что
. Очевидно, что 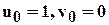 ,
,  . Сравнивая обе части на
. Сравнивая обе части на  м шаге, имеем
м шаге, имеем

Отсюда получается следующая индуктивная процедура вычисления  и
и 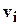 :
:
Находим  как частное от деления
как частное от деления 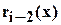 на
на 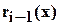 , затем вычисляем
, затем вычисляем
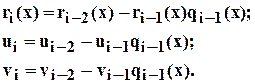
Покажем, как описанный алгоритм нахождения линейного представления наибольшего общего делителя можно реализовать в системе Mathematica.
Вводим заданные полиномы
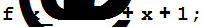
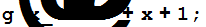
Задаём начальные значения параметров цикла
a0[x_]=f[x];a1[x_]=g[x];u0[x_]=1;v0[x_]=0;u1[x_]=0;v1[x_]=1;
q[x_]=PolynomialQuotient[a0[x],a1[x],x];
a2[x_]=a0[x]-a1[x]*q[x];u2[x_]=u0[x]-u1[x]*q[x];v2[x_]=v0[x]-v1[x]*q[x];
Находим коэффициенты линейного представления наибольшего общего делителя u1[x]и v1[x] заданных многочленов и сам наибольший общий делитель a1[x]
While[Length[CoefficientList[a2[x],x]]>0,a0[x_]=a1[x];
a1[x_]=a2[x];q[x_]=PolynomialQuotient[a0[x],a1[x],x];
u0[x_]=u1[x];u1[x_]=u2[x];v0[x_]=v1[x];v1[x_]=v2[x];
a2[x_]=Expand[a0[x]-a1[x]*q[x]];
u2[x_]=Expand[u0[x]-u1[x]*q[x]];
v2[x_]=Expand[v0[x]-v1[x]*q[x]]]
u1[x]
X
v1[x]
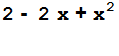
a1[x]
Проверяем правильность решения задачи
Simplify[f[x]*u1[x]+g[x]*v1[x]]
Неприводимые многочлены.
Многочлен  , отличный от постоянной, называется приводимым над числовым полем
, отличный от постоянной, называется приводимым над числовым полем 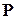 , если
, если  разлагается на произведение двух многочленов
разлагается на произведение двух многочленов 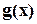 и
и 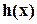 с коэффициентами из поля
с коэффициентами из поля 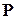 , отличных от постоянных.
, отличных от постоянных.
Если же  не может быть разложено на такое произведение, то многочлен
не может быть разложено на такое произведение, то многочлен  называется неприводимым над полем
называется неприводимым над полем 
Произвольный многочлен с коэффициентами из поля 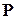 может быть записан в следующем виде
может быть записан в следующем виде
 , (3.3.1)
, (3.3.1)
где  различные многочлены, неприводимые над полем
различные многочлены, неприводимые над полем
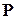 ,
, 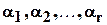 -натуральные числа.
-натуральные числа.
Может случиться, что в разложении  на неприводимые множители все
на неприводимые множители все  равны единице. В этом случае говорят, что
равны единице. В этом случае говорят, что  разлагается на однократные множители.
разлагается на однократные множители.
Говорят, что многочлен 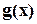 входит в
входит в  с кратностью
с кратностью  , если
, если  делится на
делится на  , но не делится на
, но не делится на 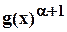 .
.
Можно доказать, что если неприводимый многочлен 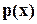 входит в
входит в  с кратностью
с кратностью  , то в производную
, то в производную  он войдёт с кратностью
он войдёт с кратностью 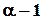 .
.
Пусть  . Обозначим через
. Обозначим через  произведение всех однократных неприводимых множителей; через
произведение всех однократных неприводимых множителей; через 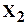 -произведение всех двукратных неприводимых множителей, взятых по одному разу, через
-произведение всех двукратных неприводимых множителей, взятых по одному разу, через 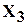 -произведение всех трёхкратных неприводимых множителей, взятых по одному разу и т.д. Может случиться, что
-произведение всех трёхкратных неприводимых множителей, взятых по одному разу и т.д. Может случиться, что  не имеет однократных множителей. Тогда будем считать, что
не имеет однократных множителей. Тогда будем считать, что 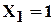 . Вообще, будем считать, что
. Вообще, будем считать, что  , если
, если  не имеет
не имеет 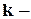 кратных множителей. Если
кратных множителей. Если 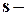 наивысшая кратность множителей многочлена
наивысшая кратность множителей многочлена 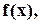 то имеет место соотношение
то имеет место соотношение
 . (3.3.2)
. (3.3.2)
Процесс построения разложения (3.3.2) называется отделением кратных множителей. Он реализуется по следующему алгоритму.
Находим 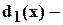 наибольший общий делитель многочлена
наибольший общий делитель многочлена  и его производной
и его производной  . Можно доказать, что
. Можно доказать, что

Наибольший общий делитель многочленов  и
и  будет равен
будет равен
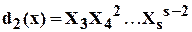 .
.
Наибольший общий делитель многочленов 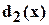 и
и  будет равен
будет равен
 .
.
Наконец получим

Далее составляем
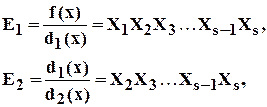

Отсюда находим
 .
.
Описанный алгоритм реализуется в системе Mathematica следующим образом.
Пример 3.3.1. Выделить кратные неприводимые множители для многочлена 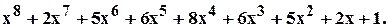
Решение.
Вводим заданный многочлен
f[x_]=x^8+2*x^7+5*x^6+6*x^5+
8*x^4+6*x^3+5*x^2+2*x+1;
Полагаем g[x] равным заданному многочлену
g[x_]=f[x];

g[x_]=PolynomialGCD[g[x],D[g[x],x]];
d=Append[d,g[x]];
While[Length[CoefficientList[g[x],x]]>1,g[x_]=
PolynomialGCD[g[x],D[g[x],x]];
d=Append[d,g[x]]];






