Пусть имеется некоторая выборочная совокупность Х объема n. Как было отмечено ранее, для каждого значения (варианта) из этой совокупности можно определить частоту и частость (относительную частоту). Пусть х – произвольное действительное число. Обозначим через nx – число вариантов из совокупности Х, значение которых строго меньше этого числа х. Тогда величина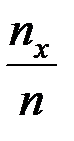 
будет определять относительную частоту значений статистической совокупности Х, меньших х, т.е. относительную частоту появления события X < x. Очевидно, что при изменении значения х в общем случае будет меняться и значение относительной частоты 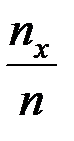. Таким образом, относительная частота является функцией аргумента х.
Эмпирической функцией распределения называется функция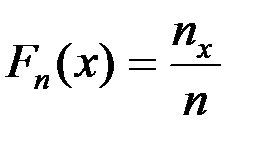 
,
где n –объем выборочной совокупности; nx – число вариант, меньших х.
Название эмпирическая связано с тем, что эта функция определяется по статистическим (выборочным) данным, т.е. опытным (эмпирическим) путем. В связи с этим обычную функцию распределения F (x) случайной величины Х иногда называют теоретической функцией распределения. Главное различие этих функций состоит в том, что теоретическая функция распределения F (x) определяет вероятность события X < x, а эмпирическая функция распределения Fn (x) - относительную частоту этого события.
Эмпирическая функция распределения при больших n часто используется для приближенного представления теоретической функции распределения, если последняя неизвестна. Возможность такого представления следует из теоремы Бернулли (см. §1.), которая доказывает, что относительная частота события в определенном смысле мало отличается от вероятности этого события при больших значениях n.
Кроме этого, необходимо также отметить, что функция Fn (x) обладает теми же свойствами, что и F (x). Действительно, из определения функции Fn (x) следует, что
1. 
.
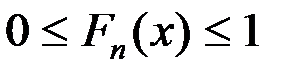2. Fn (x) является неубывающей функцией.
3. 
.
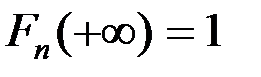Пример 4.3. Построить эмпирическую функцию для дискретного вариационного ряда из примера 4.1:
| Варианты х i | ||||
| Частоты n i |
Решение. Объем совокупности равен 10.
Наименьшее значение варианта равно 3, поэтому Fn (x) = 0, при х ≤ 3.
Значение Х < 4, а именно, х =3 наблюдалось ровно 1 раз, поэтому
Fn (x) =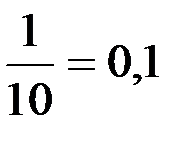 
, при 3 < х ≤ 4.
Значение Х < 6, а именно, х =3 и х = 4 наблюдалось 1 + 3 = 4 раза, поэтому Fn (x) =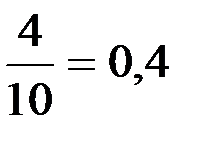 
, при 4 < х ≤ 6.
Значение Х < 9, а именно, х =3, х = 4 и х = 6 наблюдалось 1 + 3 + 5 = 9 раз, поэтому
Fn (x) =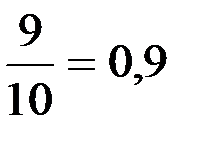 
, при 6 < х ≤ 9.
Наибольшее значение варианта равно 9, поэтому Fn (x) = 1, при х > 9.
Итак, разыскиваемая эмпирическая функция имеет вид
График этой функции выглядит следующим образом:
| 0,9 |
| 0,4 |
| Fn |
| x |
| 0,1 |
| 3 4 6 9 |
■
Дискретный вариационный ряд распределения относительных частот статистических данных является выборочным аналогом ряда распределения дискретной случайной величин. Из примера 3 видно, что и метод построения и вид эмпирической функции распределения очень похож на теоретическую функцию распределения дискретной случайной величины. Естественно возникает вопрос: Какой вид будет иметь эмпирическая функция распределения для интервального вариационного ряда? Попытаемся ответить на этот вопрос, используя интервальный ряд из примера 4.2.
Пример 4.4. Построить эмпирическую функцию распределения для следующего интервального ряда
| Интервалы | 2,5-19,5 | 19,5-36,5 | 36,5-53,5 | 53,5-70,5 | 70,5-87,5 | 87,5-104,5 |
| Частоты |
Решение. Объем статистической совокупности равен 50 единиц. Очевидно, что при всех 
функция Fn (x) =0. Предположим теперь, что 
. Для каждого такого конкретного значения х относительную частоту события X < x, т.е. функцию Fn (x) определить невозможно, так как неизвестно, сколько и каких значений вариант имеется внутри рассматриваемого интервала. Однако известно их общее число, равное 6. Следовательно, имеется 6 вариант, значения которых будут меньше правой границы рассматриваемого интервала, т.е. 19,5. Отсюда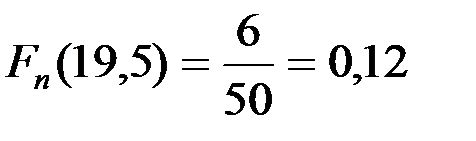 
. Рассуждая аналогично относительно остальных интервалов, убеждаемся в том, что значение функции Fn (x) можно точно определить во всех правых границах интервалов, а именно
. ■
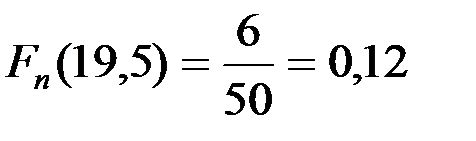
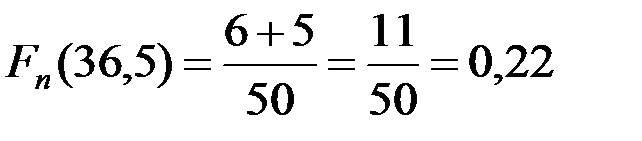
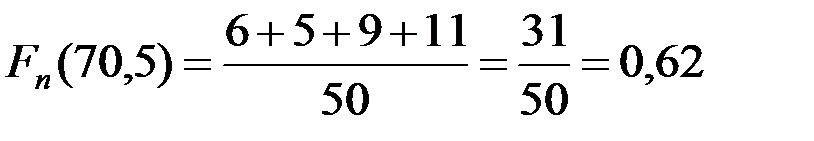
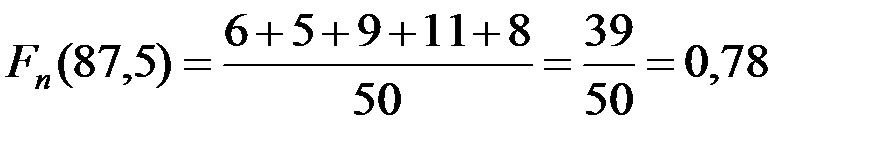
Итак, значения эмпирической функции распределения для статистических данных, записанных в виде интервального ряда, могут быть определены точно только в нескольких конкретных точках – правых границах частичных интервалов. При построении графика этой функции, ее доопределяют в остальных точках х, соединив построенные точки прямыми линиями. Для примера 4.4 график функции будет иметь вид:
| Fn 0,78 0,62 0,4 0,22 0,12 |
| 2,5 19,5 36,5 53,5 70,5 87,5 104,5 |
| x |
График эмпирической функции распределения для непрерывного вариационного ряда будет представлять собой непрерывную линию, вид которой почти такой же как и график теоретической функции распределения непрерывной случайной величины. Графики этих функций будут еще более похожими, если построенные точки соединять не прямыми линиями, а некоторой плавной кривой.
