Просторовий рух літака.
Рух літального апарату в просторі визначається з урахуванням поступальної ходи центру мас і обертального руху відносно центру мас. При записі диференціальних рівнянь руху в проекціях на осі нерухомої системи координат виникають труднощі проектування сил і моментів, які діють на літак, на осі нерухомої системи координат. До того ж сильно ускладнюється подальший аналіз таких рівнянь. Тому в динаміці польоту віддають перевагу рівнянням рухи, які записані в рухливих системах координат.
При отриманні рівнянь просторового руху приймаються такі спрощення:
- літак є абсолютно жорстким тілом з постійними інерційно-масовими характеристиками;
- осі пов'язаної системи координат співпадають з головними осями інерції, тобто отцентровые моменти інерції дорівнюють нулю;
- вектор тяги прикладений до центру мас і не утворює додаткових моментів;
- земля плоска, не обертається і не переміщається в інерціальному просторі, тобто, не враховуються переносні і кориолисовые сили і моменти;
- повітряний простір нерухомий.
Рівняння руху літака, як твердого тіла, можуть бути отримані із законів збереження кількості і моменту кількості рухи, які у векторній формі мають вигляд:
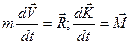, (2.1)
де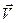 
- вектор воздушной швидкості;
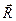- вектор зовнішніх сил, діючих на літак;
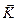- вектор момента кількості руху;
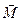- аеродинамічний момент;
- маса літака.
З векторного аналізу відомо, що похідна вектору 
у нерухомій системі координат -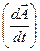 
може бути подана як сума похідної вектору в рухливій системі координат 
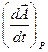і векторного твору кутової швидкості 
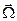обертання рухливої системи координат відносно нерухомої на вектор .
.
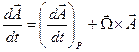У такому вигляді векторні рівняння(2.1) проектують на осі рухливих систем координат.
З урахуванням прийнятих допущень рух літака, як твердого тіла з шістьма ступенями свободи, описується шістьма рівняннями Ейлера з додаванням до цих рівнянь сил і моментів кінематичних і геометричних співвідношень, а також рівнянь, які описують траєкторний рух центру мас літака. Додаткові рівняння дозволяють замкнути систему рівнянь, яка описує просторовий рухлітака, у виді 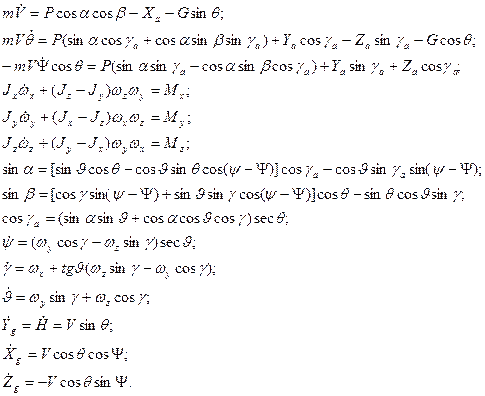(2.2).
(2.2)
У системі рівнянь просторового руху літака перші три рівняння сил розкривають закон збереження кількості руху. Ці рівняння записані в траєкторній системі координат і визначають зміни швидкості польоту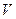 
, угла наклона траектории 
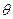и путевого угла 
под воздействием силы тяги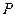 
, силы тяжести 
и аэродинамических сил: подъемной силы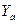 
, силы лобового сопротивления 
и боковой силы 
.
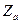При записі в траєкторній системі координат в рівняннях сил добре видима динаміка зміни параметрів польоту під дією аеродинамічних сил і, крім того, рівняння сил мають простий вигляд, оскільки вісь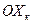 
траекторной системы координат совпадает с вектором скорости, а проекции вектора скорости на оси 
равны нулю.
Наступні три рівняння системи розкривають закон збереження моменту кількості руху. Ці рівняння записані в пов'язаній системі координат і описують зміну швидкості обертання літака під впливом аеродинамічних моментів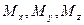 
.
При записі в пов'язаній системі координат, осі якої співпадають з головними осями інерції, рівняння моментів спрощуються, оскільки отцентровые моменти інерції 
равны нулю, и проекции момента количества движения на оси связанной системы координат имеют простой вид:
,
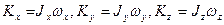де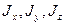 
- осевые моменты инерции;
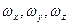- проекції вектору кутової швидкості обертання літака на осі пов'язаної системи координат.
Наступні три рівняння - це геометричні співвідношення для визначення кута атаки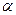 
, угла скольжения 
и скоростного угла крена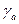 
, необхідні для визначення сил, які діють на літак, в проекціях на осі траєкторної системи координат.
Геометричні співвідношення отримані шляхом прирівнювання матриці направляючих косинусів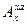 
прямого переходу від пов'язаної системи координат до швидкісної до твору матриць 
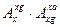послідовного переходу від пов'язаної системи координат до нормальної і далі від нормальної до швидкісної. Така процедура може бути записана у вигляді матричного рівняння.
Кінематичні співвідношення доповнюють систему рівнянь до повної і описують зміну кутів крену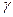 
, тангажа 
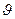и рыскания 
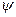. Кінематичні співвідношення отримані шляхом запису проекцій швидкостей зміни кутів крену 
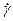, тангажа 
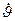и рыскания 
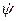(проекций угловой скорости вращения связанной системы координат вокруг нормальной) на оси связанной системы координат:
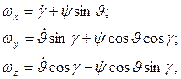
з подальшим рішенням отриманої системи рівнянь. Аналогічно для рівняння сил отримані проекції кутової швидкості обертання траєкторної системи координат навколо нормальної: 
Останні три рівняння системи потрібні для дослідження траєкторного руху літака. Окрім цього, рівняння, яке описує зміну висоти польоту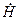 
, необхідно для виявлення функціональних залежностей аеродинамічних сил і моментів, а також тяги двигуна від щільності повітря, яка змінюється з висотою польоту.
При розкритих залежностях аеродинамічних сил і моментів, а також тяга двигуна від параметрів польоту і відомого зв'язку параметрів атмосфери з висотою польоту, система рівнянь, яка описує літак, як об'єкт управління, повністю замикається.
