Содержание
Вступ
1. Обзор синтеза законів керування ЛА
1.1. Метод аналітичного конструювання;
1.2. Метод корневого годографу;
1.3. Методи синтеза регулятора з сучасною ТАК
2. Математична модель движения самолета
2.1. Пространственное движение самолета
2.2. Вывод математической модели продольного движения самолета
2.3. Линеаризация уравнений продольного движения
2.4. Запись уравнений продольного движения
3. Синтез адаптивной системы методом функций Ляпунова
Висновки
Список літератури
Введение
Метою курсової работи є закріплення матеріала другої частини курса системи керування ЛА та освоєння модальної методики розрахунку алгоритмів керувания на прикладі синтеза закона керувания повздовжним рухом легкого беспілотного літака. Методичні вказівки вмістять вивід математичної моделі повздовжнього руха літака и створення алгоритму оптимального спостерігача.
Одним з найбільш иідповідальних і тяжких моментів при реалізаціі методики модального синтеза являєтся вибір бажаних власних значень.
Обзор методів синтеза законів керування ЛА
Метод аналитичного конструювания
Цей метод позволяє синтезувати багатомірний регулятор, враховуючий в своій структурі взаємозвязок змінних в об'єкті управління. Синтез ведеться за допомогою методів теорії оптимального або модального управління при описі об'єкту в просторі станів.
Структурна схема оптимального регулювальника стану, що містить спостерігаючий пристрій приведена на мал. Схема містить наступні елементи: Н - спостерігач; ОУ - объект керування; МОУ - модель объекта керування; ОРС - оптимальний регулятор стану, 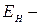 похибка спостерігача,
похибка спостерігача,  вектор стану моделі,
вектор стану моделі, 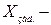 вектор задання,
вектор задання,  вектор входу ОУ,
вектор входу ОУ,  вектор виходу ОУ,
вектор виходу ОУ,  вектор виходу моделі.
вектор виходу моделі.

 ;
;  ;
;  .
.
Оптимальний регулювальник стану, будучи найбільш досконалим типом регулювальника, вимагає виміру всіх компонент вектора стану об'єкту. Для здобуття їх оцінок  використовується динамічна модель об'єкту (цифрова або аналогова), підключена паралельно вихідному ОУ. Для забезпечення рівності рухів в реальному об'єкті і моделі використовується спостерігач, який, порівнюючи рухи векторів
використовується динамічна модель об'єкту (цифрова або аналогова), підключена паралельно вихідному ОУ. Для забезпечення рівності рухів в реальному об'єкті і моделі використовується спостерігач, який, порівнюючи рухи векторів  и
и 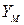 , забезпечує їх рівність
, забезпечує їх рівність  . Параметри регулювальника стану розраховуються методами аналітичного конструювання регулювальників шляхом мінімізації інтегрального квадратичного критерію
. Параметри регулювальника стану розраховуються методами аналітичного конструювання регулювальників шляхом мінімізації інтегрального квадратичного критерію
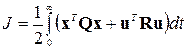 ,
,
качества де  и
и  - матриці штрафів (вагів) на компоненти вектора стану і вектора управління.
- матриці штрафів (вагів) на компоненти вектора стану і вектора управління.
Реалізація оптимального регулювальника стану найчастіше виробляється на обчислювальній машині, що управляє (УВМ).
Метод корневого годографу
На основі розташування коріння характеристичного рівняння замкнутої системи можна визначити характер перехідних процесів в системі автоматичного управління. На цих закономірностях базуються кореневі оцінки якості системи. Найпростішою кореневою оцінкою якості є міра стійкості (міра швидкодії) – відстань від уявної осі до найближчого Корню на плоскості коріння характеристичного рівняння замкнутої системи (мал. 1)
Якщо найближчим є дійсний корінь (ріс.1,а), то йому відповідає аперіодична складова рішення для перехідного процесу

(апериодина степінь стійкості  ). Час затухання визначається за формулою:
). Час затухання визначається за формулою:
 (для
(для  =5%)
=5%)
Час загасання характеризує загальну тривалість перехідного процесу, оскільки всі члени рішення, що відповідають іншому корінню, загасають швидше. 
Рис. 1. Приклад розташування коріння характеристичного рівняння п'ятого порядку замкнутої системи на комплексній плоскості: а) до уявної осі ближче знаходиться дійсний корінь; би) до уявної осі ближче знаходиться комплексне коріння.
Якщо ж найближче до уявної осі буде розташована пара комплексного коріння  (рис.1), то домінуюча складова рішення для перехідного процесу буде таким, що коливає (коливальна міра стійкості
(рис.1), то домінуюча складова рішення для перехідного процесу буде таким, що коливає (коливальна міра стійкості  ) і буде мати вигляд:
) і буде мати вигляд:

Оцінка довготривалості перехідного процесу  така сама як і в попередньому випадку (1.17).
така сама як і в попередньому випадку (1.17).
Іншою кореневою оцінкою якості є запас стійкості системи автоматичного управління. Схильність системи до коливань виявлятиметься у разі, коли у вирішенні характеристичного рівняння буде присутнє комплексне коріння вигляду  . Ця схильність може характеризуватися відношенням уявної частини кореня (кутова частота коливань) до дійсної (коефіцієнт загасання), яке називають такою, що коливає:
. Ця схильність може характеризуватися відношенням уявної частини кореня (кутова частота коливань) до дійсної (коефіцієнт загасання), яке називають такою, що коливає:
 , (1.18)
, (1.18)
де 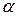 и
и  - дійсна і уявна частини коріння характеристичного рівняння. Саме ця величина характеризує швидкість загасання коливань за кожен період. Парі комплексного коріння
- дійсна і уявна частини коріння характеристичного рівняння. Саме ця величина характеризує швидкість загасання коливань за кожен період. Парі комплексного коріння  відповідає наступна складова вирішення перехідного процессу
відповідає наступна складова вирішення перехідного процессу

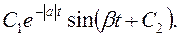
Період колебаній:
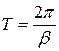
Через один період амплитуда  зменшиться до величини
зменшиться до величини
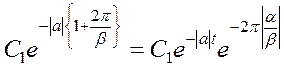
Як наслідок, чим більше коливає  , тим слабкіше відбуватимуться згасання коливань в перехідному процесі. Лінія
, тим слабкіше відбуватимуться згасання коливань в перехідному процесі. Лінія  =const утворює центральний кут
=const утворює центральний кут  (рис.2а) на комплексній плоскості, величину якого можна визначити за формулою:
(рис.2а) на комплексній плоскості, величину якого можна визначити за формулою:
 (1.19)
(1.19)
Допустимі значення степені стоікості  та колебательності
та колебательності  формуют область (рис. 2), в середині якої повинне знаходитися все коріння характеристичного рівняння замкнутої системи, що відповідають вимогам до запасу і міри стійкості.
формуют область (рис. 2), в середині якої повинне знаходитися все коріння характеристичного рівняння замкнутої системи, що відповідають вимогам до запасу і міри стійкості.
При одиничному стрибку зовнішнього впливу важливими є не лише корінні характеристичного рівняння (полюси), але і нулі передавальної функції замкнутої системи Ф(р). Значення амплітуд відхилень в перехідному процесі залежать від взаємного розташування нулів і полюсів передавальної функції замкнутої системи. Для зменшення амплітуди в перехідному процесі необхідно, щоб нулі і полюси були розташовані на незначній (мінімально можливою) відстані один від одного.
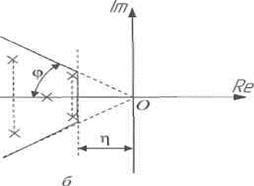
Рис. 2. Приклад розташування коріння характеристичного рівняння п'ятого порядку замкнутої системи на комплексній плоскості: а) область обмеження значень полюсів за тією, що коливає, би)область обмеження значень полюсів за швидкодією. Якість системи регуляції з точки зору швидкодії і запасу стійкості характеризується розташуванням коріння чисельника і знаменника передавальної функції замкнутої системи, тобто розташуванням нулів і полюсів передавальної функції.
Використовуючи відомі значення нулів і полюсів передавальної функції можна змалювати їх розташування на комплексній плоскості коріння. Під час розрахунку регульованої системи доцільним є відстежування змін в розташуванні коріння при зміні окремих параметрів, наприклад загального коефіцієнту посилення, постійних часу ланцюгів корекції і тому подібне, з метою встановлення оптимальних значень цих параметрів.
В разі плавної зміни значення будь-якого параметру коріння здійснюватиме переміщення на плоскості коріння по криволінійній траєкторії, яку називають кореневим годографом або траєкторією коріння. Побудувавши траєкторії всього коріння, можна вибрати таке значення змінного параметра, який відповідає найкращому розташуванню коріння.
Один із способів побудови траєкторій коріння полягає в наступному. Хай відоме диференціальне рівняння замкнутої системи, записане для регульованої величини за наявності заданого впливу:
 ,
,
где 
 (1.20)
(1.20)
Рівняння (1.17) характерне для випадку, коли впливи у вигляді обурень дорівнюють нулю, але воно може використовуватися і в разі наявності будь-яких обурень. Передавальна функція замкнутої системи:
 . (1.21)
. (1.21)
Коефіцієнти чисельника і знаменника(1.21) певним чином виражені через параметри регульованого об'єкту, регулятора і облаштування корекції. Якщо необхідно обрати величину будь-якого параметра (постійна часу, коефіцієнт посилення і тому подібне), які входять в коефіцієнти(1.21), то необхідно набути деяких постійних значень для усіх інших параметрів(наприклад, нульові значення), а для шуканого параметра  задавати різноманітні числові значення
задавати різноманітні числові значення  усередині реально можливих меж зміни цього параметра в цій системі регуляції. Для кожного варіанту необхідно вичислити корені чисельника і знаменника(1.21).
усередині реально можливих меж зміни цього параметра в цій системі регуляції. Для кожного варіанту необхідно вичислити корені чисельника і знаменника(1.21).
Якщо необхідно отримати два або декілька параметрів регульованої системи, то такі обчислення необхідно проводити кілька разів, змінюючи кожного разу один з параметрів при заданих значеннях усіх інших.






