Сучасний період розвитку теорії управління характеризується постановкою і рішенням завдань, що враховують неточність наших знань про об'єкти управління і зовнішніх обурень, що діють на них. Завдання синтезу регулятора і оцінювання стану з урахуванням невизначеності в моделі об'єкту і характеристиках вхідних дій є одними з центральних в сучасній теорії управління. Їх важливість обумовлена передусім тим, що практично у будь-якому інженерному завданні конструювання САУ є присутньою невизначеність в моделі объекта і в знанні класу вхідних обурень.
Модель реальної фізичної системи завжди буде неточною з наступних причин:
- зміна параметрів системи через ті або інші обставини;
- динамічні властивості, не враховані в моделі;
- зміна робочого режиму;
- шум датчика;
- непередбачувані зовнішні обурення.
В результаті проектувальник, перед яким стоїть завдання синтезу високоякісної системи управління через вказані обставини вимушений шукати рішення в класі робастных систем. Метою синтезу робастной системи управління є гарантія стійкості і необхідної якості незалежно від погрішностей виміру і зміни параметрів моделі. Система, що має стійкість і необхідну якість управління незважаючи на істотні невизначеності (невизначеність кінцевих розмірів (наприклад, завдання коефіцієнтів диференціального рівняння  где
где  и
и 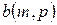 – дифференциальные операторы, интервалами с фиксированными границами) на відміну від нескінченно малих неопределенностей(які досліджуються за допомогою функцій чутливості)) в описі моделі називається робастной.
– дифференциальные операторы, интервалами с фиксированными границами) на відміну від нескінченно малих неопределенностей(які досліджуються за допомогою функцій чутливості)) в описі моделі називається робастной.
У літературі прийнято виділяти два характери неточності опису(неопределенностей) в моделі об'єкту:
- параметричні обурення(невизначеності), пов'язані з неточністю завдання коефіцієнтів диференціального рівняння;
- структурні обурення(невизначеності), пов'язані з неточністю завдання порядку диференціального рівняння.
Другий спосіб опису невизначеності системи, очевидно, є загальнішим і включає перший як окремий випадок.
Найбільш перспективними видаються методи -управления, методи, грунтовані на принципі виключення нуля, а також методи побудови меж області стійкості в просторі параметрів об'єкту, що розвиваються в роботах Неймарка Ю. И., а також в роботах Аккермана. Для зручності подальшого викладу представляється доцільним привести тут основні положення перерахованих методів.
Теорема Харитонова. Цей результат, що дістав в літературі назву "Теореми Харитонова" уперше був опублікований в 1978 році в роботі Харитонова В.Л.
У вказаній роботі розглядалося завдання дослідження стійкості(гурвицевости) сімейства поліномів виду:A (s)={A (s) = a 0 + a 1 s + … + an sn, ai >0,  £ ai £
£ ai £ 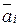 , i = 0, …, n -1 }. (1.22)
, i = 0, …, n -1 }. (1.22)
Сімейство(1.22) в літературі іменується інтервальним поліномом.
Твердження 1(теорема Харитонова). Сімейство(1.22) гурвицево тоді і тільки тоді, коли гурвицевы наступні чотири поліноми
A1 (s) = 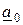 +
+  s +
s +  s 2 +
s 2 + 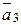 s 3 + …,
s 3 + …,
|
 +
+  s +
s +  s 2 +
s 2 + 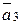 s 3 + …,
s 3 + …,
A3 (s) =  +
+  s +
s +  s 2 +
s 2 +  s 3 + …,
s 3 + …,
A4 (s) = 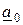 +
+  s +
s +  s 2 +
s 2 +  s 3 + ….
s 3 + ….
Поліноми(1.23) в літературі дістали назву поліномів Харитонова.
Теорема Харитонова чудова двома моментами:
1)вона уперше встановила властивості робастной стійкості(гурвицевости) з точністю до необхідних і достатніх умов;
2)дослідження інтервального полінома зводиться до дослідження гурвицевости 4-х поліномів c точно певними коефіцієнтами(поліномів Харитонова).
Особливо слід зазначити, що у багатьох роботах робилися спроби отримати подібні результати для матриць, коефіцієнти яких призначені інтервалами суть результатів яких можна звести до наступного: в загальному випадку не вдається вказати кінцевого числа матриць таких, що їх гурвицевость гарантувала б гурвицевость усіх матриць із заданого сімейства.
Принцип виключення нуля. У роботах Цыпкина Я. З. і Поляка Б. Т. був сформульований загальний підхід до дослідження робастной стійкості і робастного якості управління при досить довільному способі завдання параметричній невизначеності, що дістав назву в літературі принципу виключення нуля. Коротко, суть цього методу полягає в наступному.
Нехай характеристичний поліном досліджуваної системи має вигляд:
 , (1.24)
, (1.24)
де вектор коеффіцієнтів  належать де якій одинзв'язній множині
належать де якій одинзв'язній множині  , що лежить в напівпросторі
, що лежить в напівпросторі  :
:
 ,
,  . (1.25)
. (1.25)
Система вважається робастно стійкою, якщо усі корені усіх поліномів(1.24),(1.25) лежать в лівій напівплощині: 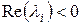 ,
,  . Розглянемо (1.24) при
. Розглянемо (1.24) при 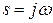 (здесь
(здесь 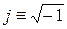 ); множина значень
); множина значень 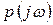 на комплексній площині при фіксованому
на комплексній площині при фіксованому 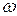 , коли коэфіцієнти
, коли коэфіцієнти  приймають значення з (1.25) позначимо
приймають значення з (1.25) позначимо  :
:
 .
.
Хай  ,
,

- "необурений" поліном.
Твердження 2. Система робастно стійка тоді і тільки тоді коли  гурвицев и
гурвицев и  для усіх
для усіх  .
.
Це твердження іноді іменується в літературі принципом виключення нуля.
Методи  -керування стосовно дослідження властивостей робастной стійкості в цілому зводяться до наступного результату.
-керування стосовно дослідження властивостей робастной стійкості в цілому зводяться до наступного результату.
Розглянемо замкнуту систему управління, що складається з об'єкту управління і регулятора; нехай передатна функція об'єкту має вигляд:
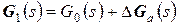 , (1.26) тут за
, (1.26) тут за  позначена передатна функція необуреного об'єкту, а:
позначена передатна функція необуреного об'єкту, а:
 , (адаптивний тип невизначеності),
, (адаптивний тип невизначеності),
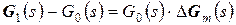 , (мультипликативний тип невизначеності).
, (мультипликативний тип невизначеності).
Передбачається, що передатна функція замкнутої системи з номінальним об'єктом  і регулятором
і регулятором 

стійка; використовуючи(1.26) запишемо рівняння замкнутої системи ( ;
;  ) з урахуванням невизначеності:
) з урахуванням невизначеності:
 , (1.27)
, (1.27)
 .
.
Твердження 3. Системи(1.27) стійкі, якщо виконуються відповідно умови
 , (1.28)
, (1.28)
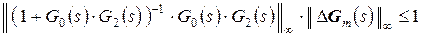 .
.
Тут за  обозначена
обозначена  –норма оператора
–норма оператора  , яка визначена наступним чином
, яка визначена наступним чином
 ,
, 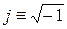 .
.
З співвідношень (1.28) витікають наступні обмеження на  і
і 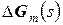 :
:
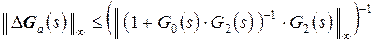 ,
,
 .
.
Викладений критерій має велику спільність формулювання, він дозволяє із загальних позицій розглядати в моделі об'єкту разом з параметричною структурною невизначеністю. Проте за цю спільність доводиться платити достатністю критерію(1.28) (тут доречно порівняти цей критерій з відомим з курсу теорії автоматичного управління критерієм Найквіста).






