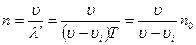25. Уравнение плоской волны.
Пусть точки, которые расположены в плоскости х = 0, колеблются по закону 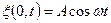 . И пусть υ— скорость распространения колебаний в данной среде.
. И пусть υ— скорость распространения колебаний в данной среде.
Колебания частицы В среды (см. рисунок), расположенной на расстоянии х от источника колебаний О, будут происходить по тому же закону. Но, поскольку для прохождения волной расстояния х требуется время 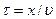 , то ее колебания будут отставать по времени от колебания источника на τ.
, то ее колебания будут отставать по времени от колебания источника на τ.
Уравнение колебаний частиц, лежащих вплоскости х, имеет вид

 Следовательно, функция
Следовательно, функция 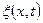 является не только периодической функцией времени, но и периодической функцией координаты х.
является не только периодической функцией времени, но и периодической функцией координаты х.
В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид
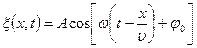
здесь: А = const — амплитуда волны,
ω — циклическая частота,
 — начальная фаза волны,
— начальная фаза волны,
 — фаза плоской волны.
— фаза плоской волны.
Если определить волновое число:

то уравнение плоской бегущей волны можно записать в виде
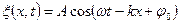
или в экспоненциальной форме
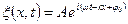
где физический смысл имеет только вещественная часть.
В общем виде уравнение плоской волны, распространяющейся в направлении  имеет вид:
имеет вид:
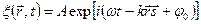
25. Фазовая скорость.
Скорость  в этих уравнениях есть скорость распространения фазы волны и ее называют фазовой скоростью.
в этих уравнениях есть скорость распространения фазы волны и ее называют фазовой скоростью.
Действительно, пусть в волновом процессе фаза постоянна:
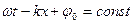
откуда

26. Уравнение сферической волны.

где r — расстояние от центра волны до рассматриваемой точки среды. Амплитуда колебаний в сферической волне убывает с расстоянием по закону 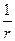 .
.
27. Волновое уравнение.
Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных:
 или
или 
где υ - фазовая скорость,
 — оператор Лапласа.
— оператор Лапласа.
Решением волнового уравнения является уравнение любой волны (в том числе и плоская и сферическая волны).
Волновое уравнение для плоской волны, распространяющейся вдоль оси х:

28. Принцип суперпозиции.
Если среда, в которой распространяется одновременно несколько волн, линейна, то к этим волнам применим принцип суперпозиций (наложения) волн:
при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвующие в каждом из слагающих волновых процессов.
29. Групповая скорость.
Любое сложное колебание может быть представлено в виде суммы одновременно совершающихся гармонических колебаний (разложение Фурье).
Поэтому любая волна может быть представлена в виде суммы гармонических волн, то есть в виде волнового пакета или группы волн.
Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства.
За скорость распространения волнового пакета принимают скорость перемещения максимума его амплитуды (центра волнового пакета).
Групповой скоростью и называется скорость движения группы волн, образующих в каждый момент времени локализованный в пространстве волновой пакет (или скорость движения центра волнового пакета).
Ее величина
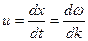
Связь групповой и фазовой скоростей:
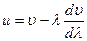
30. Интерференция волн.
Когерентностью называется согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов.
Две волны называются когерентными, если разность их фаз не зависит от времени.
Гармонические волны, имеющие одинаковую частоту, когерентны всегда.
Интерференцией волн называется явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих волн.
Рассмотрим наложение двух когерентных сферических волн, возбуждаемых точечными источниками, колеблющимися с одинаковыми амплитудой 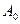 , частотой ωи постоянной разностью фаз:
, частотой ωи постоянной разностью фаз:
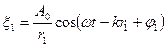 ,
, 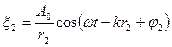
где  и
и  — расстояния от источников до рассматриваемой точки, k —
— расстояния от источников до рассматриваемой точки, k —
волновое число,  — начальные фазы волн.
— начальные фазы волн.
Амплитуда результирующей волны

Поскольку для когерентных источников 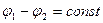 , то результат интерференции двух волн зависит от величины
, то результат интерференции двух волн зависит от величины  , называемой разностью хода.
, называемой разностью хода.
Интерференционный максимум  наблюдается в точках, где
наблюдается в точках, где 

Числа  называются порядком интерференционного максимума.
называются порядком интерференционного максимума.
наблюдается в точках,
Интерференционный минимум  наблюдается в точках, где
наблюдается в точках, где 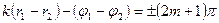
 .
.
Числа  называются порядком интерференционного минимума.
называются порядком интерференционного минимума.
31. Стоячие волны.
Особым случаем интерференции являются стоячие волны.
Стоячие волны — это волны, образующиеся при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Пусть две плоские бегущие волны с одинаковыми амплитудами и частотами распространяются навстречу друг другу вдоль оси х:
 ,
, 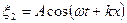
Сложив эти уравнения, с учетом 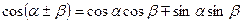 и
и  получим уравнение стоячей волны:
получим уравнение стоячей волны:
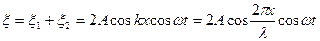

В точках среды, где 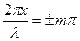 (т =0,1, 2,...) амплитуда стоячей волны достигает максимального значения
(т =0,1, 2,...) амплитуда стоячей волны достигает максимального значения 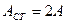 . Такие точки называются пучностями стоячей волны.
. Такие точки называются пучностями стоячей волны.
Координаты пучностей:

В точках среды, где 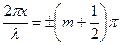 (т = 0,1,2,...), амплитуда стоячей обращается в нуль
(т = 0,1,2,...), амплитуда стоячей обращается в нуль 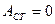 . Такие точки называются узлами стоячей волны.
. Такие точки называются узлами стоячей волны.
Координаты узлов: 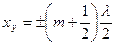 (m=0,1,2,…).
(m=0,1,2,…).
Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины волны λ бегущих волн. Эту
величину называют длиной стоячей волны:  .
.
| В бегущей волне | В стоячей волне |
| Амплитуда колебаний | |
| все точки волны совершают колебания с одинаковой амплитудой | все точки между двумя узлами колеблются с разными амплитудами |
| Фаза колебаний | |
| фаза колебаний зависит от координаты х рассматриваемой точки | все точки между двумя узлами колеблются с одинаковыми фазами |
| при переходе через узел фаза колебаний изменяется на π; точки лежащие по разные стороны от узла колеблются в противофазе | |
| Перенос энергии | |
| энергия колебательного движения переносится в направлении распространения бегущей волны | переноса энергии нет, лишь впределах  происходят взаимные превращения кинетической энергии в потенциальную и обратно происходят взаимные превращения кинетической энергии в потенциальную и обратно
|
Образование стоячих волн наблюдают при интерференции бегущей и отраженной волн.
Если среда, от которой происходит отражение, менее плотная, то на границе сред образуется пучность.
Если среда, от которой происходит отражение, более плотная, то на границе сред образуется узел стоячей волны.
32. Эффект Доплера.
Эффектом Доплера называется изменение частоты колебаний, воспринимаемой приемником, при движении источника этих колебаний и приемника друг относительно друга. В акустике эффект Доплера проявляется как повышение тона при приближении источника звука к приемнику и понижения тона звука при удалении источника от приемника.
Пусть источник и приемник звука движутся вдоль соединяющей их прямой; 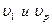 — скорости источника и приемника (положительны при сближении и отрицательны при удалении источника и приемника); п0 — частота колебаний источника; υ — скорость распространения звука в данной среде.
— скорости источника и приемника (положительны при сближении и отрицательны при удалении источника и приемника); п0 — частота колебаний источника; υ — скорость распространения звука в данной среде.
1)Источник и приемник покоятся относительно среды:  .
.
Длина волны  . Распространяясь в среде, волна достигнет приемника и вызовет его колебания с частотой:
. Распространяясь в среде, волна достигнет приемника и вызовет его колебания с частотой: 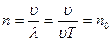 .
.
2)Приемник приближается к источнику, а источник покоится:
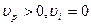 . Скорость распространения волны относительно приемника станет равной
. Скорость распространения волны относительно приемника станет равной 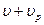 , при этом длина волны не меняется, следовательно
, при этом длина волны не меняется, следовательно

Частота колебаний, воспринимаемых приемником увеличится.
3)Источник приближается к приемнику, а приемник покоится:

 . Скорость распространения колебаний υ зависит только от свойств среды, поэтому за время, равное периоду колебаний источника, излученная им волна пройдет в направлении к приемнику расстояние
. Скорость распространения колебаний υ зависит только от свойств среды, поэтому за время, равное периоду колебаний источника, излученная им волна пройдет в направлении к приемнику расстояние  . Источник же пройдет расстояние
. Источник же пройдет расстояние 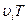 . Поэтому к моменту окончания излучения волны длина волны в направлении движения сократится и станет
. Поэтому к моменту окончания излучения волны длина волны в направлении движения сократится и станет 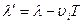 . Частота колебаний которые воспринимает приемник, увеличится:
. Частота колебаний которые воспринимает приемник, увеличится: