При движении тела в вязкой жидкости возникают силы сопротивления. Происхождение этого сопротивления двояко. При небольших скоростях когда за телом нет вихрей, сила сопротивления обусловливается вязкостью жидкости. Слой жидкости, прилегающие к телу, увлекаются им. Между этими слоями и следующими возникают силы трения. Второй механизм сил сопротивления связан с образованием вихрей, энергия которых переходят в теплоту. Рассмотрим движение тела в вязкой жидкости. В этом случае очень тонкий слой жидкости прилипает к поверхности тела и движется с ним как одно целое, увлекая за собой из-за внутреннего трения последующие слои. По мере удаления от поверхности тела скорость слоев становится все меньше и на некотором расстоянии от поверхности жидкость будет не возмущенной движением тела. Таким образом, тело оказывается окруженным слоем жидкости с быстро изменяющейся внутри него скоростью.
В этом случае действуют силы вязкого трения, приложенные к телу и приводят к возникновению лобового сопротивления (см. Рис.2).
Английский физик и математик Стокс установил, что сила сопротивления движению в жидкостях небольших шариков при малых скоростях равна.
(4)
Здесь 
– радиус шара, 
– скорость движения шара, 
– вязкость жидкости, 
– сила трения (сопротивления).
На движущийся шарик в жидкости действуют три силы: 1) сила тяжести шарика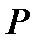 
, направленная вертикально вниз; 2) подъемная сила 
(по закону Архимеда равная весу вытесненной шариком жидкости), направленная вверх, 3) сила трения (сопротивления) 
– направленная вверх. Возникновение этой силы обусловлено не трением шарика о жидкость, а связано с движением самой жидкости. Слои жидкости увлекаемые шариком, приходят вместе с ним в движение. Скорость этих слоев убывает с расстоянием. Наличие градиента скорости и вызывает появление между слоями жидкости сил внутреннего трения 
.
Силу тяжести и выталкивающую силу определяют через объем шарика:
(5)
(6)
r – плотность шарика и r1 – плотность жидкости.
Сила тяжести и выталкивающая сила постоянны, а сила сопротивления прямо пропорциональна скорости. При движении шарика в жидкости наступает момент, когда все три силы уравновешиваются, и шарик начинает двигаться равномерно: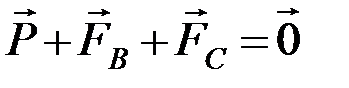 
или в скалярной форме Р = FB + FC подставляя (4), (5) и (6) в эту формулу получим:
Откуда
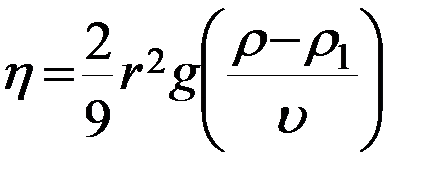(7)
где 
и 
– плотность шарика и жидкости, соответственно равные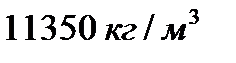 
и 
; 
– объем шарика; 
– масса шарика; 
– ускорение силы тяжести, равное 
; 
– радиус шарика.
В данной работе измеряется коэффициент вязкости масла налитого в стеклянный цилиндр 
. На стенках цилиндра нанесены метк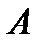и 
и 
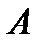. Верхняя метка должна быть на таком расстоянии от уровня исследуемой жидкости, чтобы шарик к моменту прохождения метки успел приобрести постоянную скорость.
Порядок выполнения работы
1. Установить стеклянный цилиндр по отвесу.
2. Измерить диаметр шарика при помощи микрометра.
3. Установить верхнюю метку 
, бросая шарик в цилиндр вдоль его оси. 4. Верхняя отметка должна быть на 
ниже уровня жидкости, чтобы шарик успел приобрести постоянную скорость 
.
5. Определить скорость равномерного падения шарика 
.
Для этого измерить расстояние между двумя метками и опустив шарик в цилиндр определить при помощи секундомера время 
прохождения шариком этого расстояния.
6. Вычислить коэффициент вязкости по формуле (7).
7. Вычислить погрешность измерения по формуле (8)
.
Вычислить абсолютную погрешность по известной относительной погрешности 
8. Результаты измерений и вычислений занести в таблицу
| № | 
| 
| 
| 
| 
| 
| 
| 
| 
|
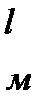
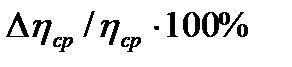
| Ср. |
9.Окончательный результат измерений записать в виде:
10.В отчете указать температуру, при которой производилось измерение коэффициента вязкости и сделать анализ результатов.
Контрольные вопросы
1. Какие процессы называют явлениями переноса?
2. Объяснить механизм возникновения вязкости (сил внутреннего трения) из молекулярно– кинетической теории.
3. Дать определение вязкости.
4. В каких единицах измеряется вязкость в системе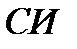 
?
5. Какие силы действуют на шарик при его движении в жидкости, и какова природа этих сил?
6. В чем суть метода Стокса?
Лабораторная работа 3
