Для определения коэффициента внутреннего трения или вязкости газов используется формула (13) французского физика Пуазейля, установленная для потока жидкости, когда его течение по трубам ламинарно. При этом скорость частиц жидкости изменяется от нуля в непосредственной близости к стенкам трубы максимума на оси трубы. (рис 4).
Жидкость при этом оказывается как бы разделенной на тонкие цилиндрически слои, которые скользят друг относительно друга, не перемешиваясь(рис. 5.).
На рис. 5 показано поперечное сечение трубы, в которой течет жидкость или газ. Штриховые окружности – условные границы между слоями, движущимися с разными скоростями u; 
– площадка на границе между слоями. Направление z перпендикулярно к площадке S.
Поток жидкости 
, т.е. объем жидкости протекающей через поперечное сечение трубы в единицу времени, вычисляется по формуле Пуазейля:
(13)
Из этой формулы следует, что поток Q очень сильно зависит от радиуса трубы r. Естественно, что поток 
пропорционален отношению 
, т.е. перепаду давления на единице длины трубы, а так же обратно пропорционален вязкости жидкости 
.
Формула Пуазейля используется для определения вязкости жидкостей и газов. Пропуская жидкость или газ через трубку известного радиуса, измеряют перепад давления и поток 
. Затем на основании полученных данных вычисляют 
.
В настоящей работе определяется вязкость (коэффициент внутреннего трения) газа. При этом в формуле Пуазейля принимает такой вид:
(14)
Здесь поток 
заменен объем 
газа (воздуха) прошедшего за время t через трубку длиной l и радиусом R. 
– разность давлений на концах трубки.
Среднюю длину свободного пробега молекул воздуха найдем из формулы (12) т.е.
(15)
Среднеарифметическая скорость выражается формулой:
(16)
где 
– универсальная газовая постоянная, равная 
; μ- молярная масса воздуха, равная 
; 
– термодинамическая температура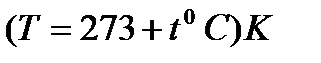 
.
Из уравнения Клапейрона – Менделеева найдем плотность газа:
(17)
Из выражений (15), (16) и (17) следует, что
(18)
Установка, используемая в данной работе, показана на 
.
Порядок выполнения работы
1. Аспиратор наполняют водой до отмеченной метки 
.
2. Открывают кран 5, в результате давление в аспираторе понижается и через капилляр засасывается воздух, проходящий через осушительный фильтр.
3. Когда, установится стационарное течение (при этом разность уровней жидкости в манометре будет постоянной), включить секундомер.
4. После того, как вытечет 1 или 1,5л воды, выключить
секундомер и определить 
.
5. Измерить 
, и 
, в 
.
6. Измерить длину 
и диаметр 
капилляра, а затем определить
его радиус 
(для нашей установки 
).
7. Измерить температуру воздуха.
8. Объем воздуха 
, прошедшего за время 
через капилляр, определяется по шкале аспиратора, градуированной в литрах.
9. Измерения произвести три раза.
10. Разность давлений 
на концах капилляра определяется по формуле 
, где 
– плотность воды, равная 
;
- ускорение силы тяжести, равное 
.
11. Вычислить коэффициент внутреннего трения по формуле(14).
12. Вычислить среднюю длину свободного пробега по формуле (18).
13. Вычислить погрешности измерений 
по формулам:
(19)
(20)
Здесь погрешности заданных величин 
не учтены.
14.Вычислить 
по формулам: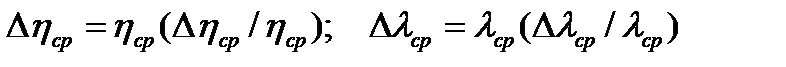 
.
15. Все измерения и вычисленные величины записать в таблицу.
| № | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| |||
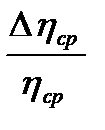
| Ср | |||||||||||||||
16.Окончательный результат измерений записать вследующем виде:
Контрольные вопросы.
1. Как понимаете процесс столкновений молекул друг с другом?
2. Какие силы действуют между молекулами?
3. Что такое эффективный диаметр и эффективное сечение молекулы?
4. Как определяется число соударения молекул?
5. Что такое средняя длина свободного пробега молекул и по какой формуле она определяется?
6. Напишите основное уравнение молекулярно–кинетической теории для давления?
7. Напишите опытный закон Ньютона для вязкости и коэффициент вязкости, полученный из молекулярно–кинетической теории.
8. В каких единицах измеряется коэффициент вязкости в системе СИ?
Лабораторная работа 2
