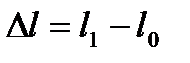
лин.деформация
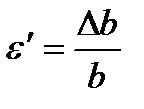поперечн.деф-ия
- закон Гука
Е= 2*107 МПа для констр. мат. модуль упругости 1 рода
- коэф. Пуассона = 0,3 для констр.мат.
41. Виды расчётов на прочность при «растяжении-сжатии»: проектный, проверочный, расчёт допускаемой нагрузки.
Условие прочности 
или 
Под 
следует понимать наибольшее расчетное напряжение.
Незначительное превышение наибольших расчетных напряжений над допускаемыми, конечно, не опасно, так как допускаемое напряжение составляет лишь некоторую часть от предельного. Обычно до 3%.
В зависимости от цели расчета (постановки задачи) различают три вида расчетов на прочность: I) проверочный, 2) проектный и 3) определение допускаемой нагрузки.
1. При проверочном расчете нагрузка бруса, его материал (а следовательно, допускаемое 
или предельное напряжение 
) и размеры известны. Определению подлежит наибольшее расчетное напряжение, которое сравнивают с допускаемым. С проверочными расчетами встречаются при экспертизе выполненных проектов.
Расчетная формула (условие прочности при растяжении или сжатии) имеет вид
(19.1)
где 
– напряжение, возникающее в опасном поперечном сечении бруса (опасным называют сечение, для которого коэффициент запаса прочности имеет наименьшее значение); N – продольная сила в указанном сечении; A – площадь опасного поперечного сечения; 
– допускаемое напряжение (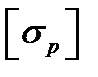
при растяжении и 
при сжатии).
В ряде случаев при проверочном расчете удобнее сопоставлять не расчетное напряжение с допускаемым, а сравнивать расчетный коэффициент запаса прочности для опасного сечения с требуемым, т.е. проверять, соблюдается ли неравенство
2. При проектном расчете нагрузки и материал (допускаемые напряжения) известны и определяют требуемую площадь сечения бруса А.
3. В некоторых случаях проверочный расчет удобнее вести в форме определения допускаемой нагрузки. Это целесообразно, когда возникает необходимость в повышении нагрузок существующего оборудования и, следовательно, надо знать их предельно допускаемое по условию прочности значение.
При этом расчете размеры бруса и его материал (допускаемое напряжение) известны, определению подлежит нагрузка, которую можно допустить по условию его прочности. Определяют допускаемое значение продольной силы [N]. По этому значению с помощью метода сечений определяют допускаемое значение внешних сил - нагрузок.
42.Вид нагружения «сдвиг», расчеты напряжений и перемещений при сдвиге
Вид нагружения Схема нагружения
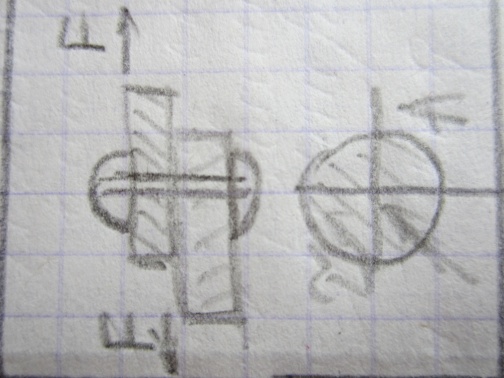
Расчетные зависимости Оценка прочности
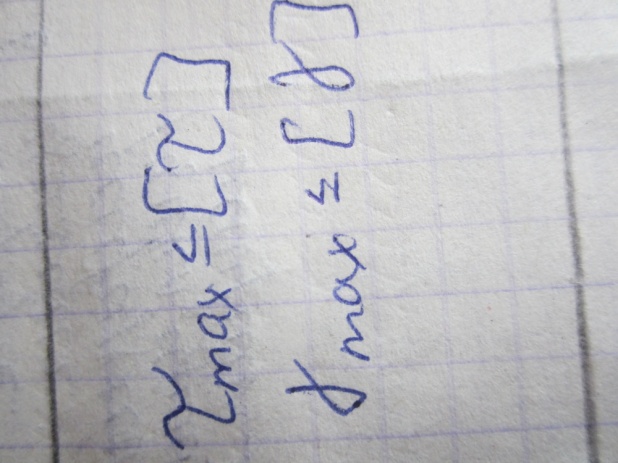
43. Вид нагружения «кручение» расчет на прочность при кручении.
Кручение– это такой вид деформации бруса, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор –крутящий момент, обозначаемый 
или 
.
На рис. 19.13 изображен брус, работающий на кручение под действием приложенных к нему скручивающих моментов (M1, M2, M3, М4).
Во всех случаях будем считать, что алгебраическая сумма скручивающих моментов равна нулю, т.е. брус находится в равновесии.
Применяя метод сечений и рассматривая равновесие оставленной части (рис. 19.14), приходим к выводу, что внутренние силы, возникающие в поперечном сечении бруса, должны дать момент (крутящий момент), уравновешивающий внешние моменты,приложенные к оставленной части.
Итак, крутящий момент, возникающий в произвольном поперечном сечении бруса, численно равен алгебраической сумме скручивающих моментов, приложенных к оставленной части.
При кручении бруса в его поперечных сечениях возникают только касательные напряжения.
Для расчета на прочность, так же как и при растяжении (сжатии) бруса, надо найти его опасное сечение. В случае, если размеры поперечного сечения по длине бруса постоянны, опасными будут сечения, в которых крутящий момент максимален. График, показывающий закон изменения крутящих моментов по длине бруса, называется эпюрой крутящих моментов.
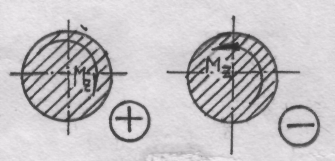
Правило знаков: будем считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется направленным по часовой стрелке (рис.19.15). Соответствующий внешний момент направлен против часовой стрелки.
Расчеты на прочность и жесткость при кручении.
Прочность бруса, работающего на кручение, считают обеспеченной, если наибольшие касательные напряжения, возникающие в его опасном сечении, не превышают допускаемых:
Конечно, незначительное (до 5...6%) превышение расчетного напряжения над допускаемым не опасно.
Эпюры касательных напряжений для круглого сплошного и кольцевого поперечных сечений показаны на рис. 19.16.
точках, равноудаленных от центра сечения, напряжения одинаковы.
Наибольшего значения касательные напряжения достигают в точках контура поперечного сечения.
где 
– полярный момент инерции.
Введя обозначение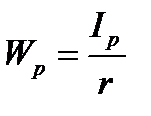 
, получим следующее выражение для максимального касательного напряжения: 
(19.12)
Величину 
(мм3), равную отношению полярного момента инерции сечения к его радиусу, называют полярным моментом сопротивления сечения. Его размерность – L3. Очевидно, полярный момент сопротивления является геометрической характеристикой прочности бруса круглого поперечного сечения при кручении.
(19.13)
Эта формула служит для проверочного расчета на прочность.
При проектном расчете и при определении допускаемой нагрузки (момента) из формулы (19.13) соответственно находят или 
Для кольца: 
;
(19.14)
и для круга: 
(19.15)
Для конструкционной углеродистой стали обычно 
= 20..35 МПа.
44. Перемещения при кручении, их оценка, расчёт валов на прочность.
Во многих случаях вал должен быть рассчитан не только на прочность, но и на жесткость при кручении.
Рассмотрим брус, жестко защемленный одним концом и нагруженный на свободном конце скручивающим моментом М (рис. 19.17). При деформации 
бруса его поперечные сечения повернутся на некоторые углы по отношению к своему первоначальному положению или, что то же, по отношению к неподвижному сечению (заделке). Угол поворота будет тем больше, чем дальше отстоит данное сечение от заделки. Так, для произвольного сечения I, отстоящего от заделки на расстоянии Z, он равен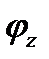 
, для сечения II– 
.Здесь 
– угол поворота сечения II относительно I или угол закручивания элемента бруса длиной 
.
Вообще угол поворота произвольного сечения равен углу закручивания части бруса, заключенной между этим сечением и заделкой. Таким образом, угол поворота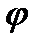 
торцового сечения представляет собой полный угол закручивания рассматриваемого бруса.
За меру жесткости при кручении принимают относительный угол закручивания (угол закручивания на единицу длины) вала, обозначаемый 
(встречается обозначение 
).
(19.16)
Угол закручивания бруса постоянного диаметра при одинаковом во всех поперечных сечениях крутящем моменте равен
(19.17)
где l – длина рассматриваемого участка, мм.
В отличие от допускаемого напряжения, зависящего в первую очередь от материала вала, допускаемый угол закручивания зависит от назначения вала.
Значения допускаемых углов закручивания, встречающихся в различных отраслях машиностроения, весьма разнообразны; наиболее распространены значения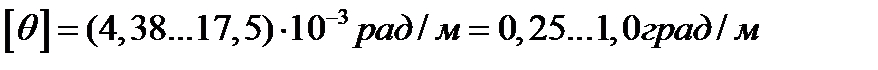 
Условие жесткости при кручении имеет вид
(19.18)
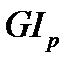– условно жесткость сечения круглого бруса при кручении. Модуль сдвига (G) характеризует жесткость материала, а полярный момент инерции () является геометрической характеристикой жесткости бруса.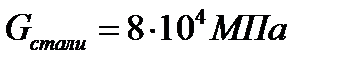 
При проектном расчете отсюда определяют требуемое значение , а затем по формуле (19.19) или (19.20) вычисляют диаметр вала. Из двух значений диаметра вала,
определенных из расчетов на прочность и жесткость, в качестве окончательного (исполнительного размера) должен быть, конечно, принят больший.
(19.19)
Для круга 
45. Вид нагружения «изгиб», внутренние силы, напряжения, их оценка.
