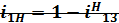Зубчатая передача – это трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими между собой высшую пару. Зубчатые передачи – самый распространенный вид механических передач.В зависимости от расположения осей вращения колес различают следующие виды зубчатых передач: 1) с параллельными осями (цилиндрические); 2) с пересекающимися осями (конические); 3) со скрещивающимися осями (гипоидные). Цилиндрические передачи относятся к плоским механизмам, а конические и гипоидные – к пространственным.Зубчатое колесо передачи с меньшим числом зубьев называется шестерней, а с большим числом зубьев – колесом. Отношение числа зубьев колеса (Z2) к числу зубьев шестерни (Z1) называется передаточным числом: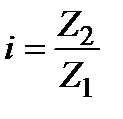 
.По соотношению угловых скоростей ведущего и ведомого звень-ев зубчатые передачи делятся на: а) понижающие (редукторы) и б) повышающие (мультипликаторы). У понижающих передач ведомое звено вращается с меньшей скоростью, чем ведущее, а у повы-шающих – наоборот.Основным кинематическим параметром зубчатого механизма является передаточное отношение.Передаточным отношением 
называется отношение угловой скорости звена 1 (w1) к угловой скорости звена 2 (w2).
или 
.Если 
и 
: 
и 
,где n1 и n2 – частота вращения, мин-1, звена 1 звена 2.
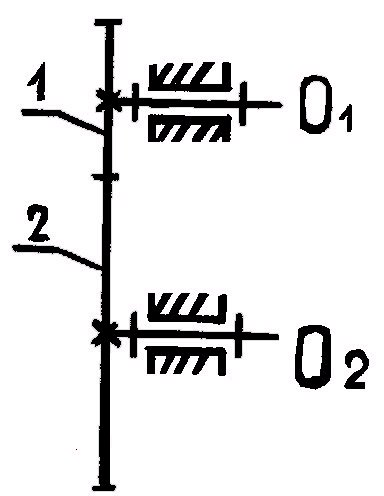
Для механизмов с параллельными осями передаточное отношение считается положительным при одинаковом направлении угловых скоростей и отрицательным – при противоположном.Для цилиндрической передачи знак «плюс» соответствует внутреннему зацеплению а «минус» – внешнему.Передаточное отношение можно представить в виде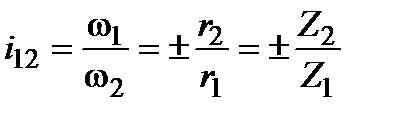 
. передаточное отношение многоступенчатой передачи равно произведению передаточных отношений отдельных ступеней.Направление вращения колес можно определить с помощью стре-лок, поставленных на схеме механизма. Многоступенчатый зубчатый механизм можно образовать последовательным соединением колес. Передаточное отношение червячной передачи равно отношению числа зубьев колеса к числу витков червяка: 
,где Z2 – число зубьев червячного колеса; Z1 – число витков червяка; n1 и n2 – частота вращения червяка и колеса, мин-1.Знак для общего передаточного отношения ставят лишь в том случае, когда входной и выходной валы вращаются относительно осей, параллельных друг другу.
Планетарные и дифференциальные механизмы
В практике применяются зубчатые механизмы, имеющие колеса с подвижными геометрическими осями (сателлиты). Такие механизмы называются планетарными (если имеют одну степень свободы) или дифференциальными (если степень свободы равна двум).
Планетарные и дифференциальные механизмы позволяют получить более высокий кинематический эффект, более высокий кпд, более удобную компоновку. Дифференциальные механизмы позволяют также раскладывать одно движение на два или складывать два движения в одно.
а) б)
Рисунок 37
На рисунке 37 приведен пример дифференциального (рисунок 37 а) и планетарного механизмов (рисунок 37 б). В этих механизмах колесо "2" имеет подвижную геометрическую ось – это и есть сателлит.
Неподвижная геометрическая ось, вокруг которой движется ось сателлита, называется центральной осью. Колеса, геометрические оси которых совпадают с центральной, также называются центральными (на рисунке 37 колеса "1" и "3" – иногда такие колеса называют солнечными). Звено, соединяющее ось сателлитов с центральной осью, называется водилом (водило обычно обозначается "H").
При кинематическом исследовании дифференциальных и планетарных механизмов применяется метод обращения движения (по-другому его называют методом остановки водила). Смысл этого метода заключается в том, что если всем звеньям системы добавить (с любым знаком) одну и ту же скорость, то характер относительного движения этих звеньев не изменится.
Передаточное отношение планетарного механизма определяется формулой Виллиса: 
