ЧАСТЬ 1. МЕХАНИКА
Глава 1. КИНЕМАТИКА: ФИЗИЧЕСКИЕ МОДЕЛИ, СИСТЕМЫ ОТСЧЁТА, ЛИНЕЙНАЯ СКОРОСТЬ, ЗАКОН ИНЕРЦИИ И ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ, ПЕРВЫЙ ЗАКОН НЬЮТОНА
1. Каково понимание пространства и времени у нас?
2. Что такое физическая модель, материальная точка, абсолютно твердое тело, сплошная среда?
3. Чем занимается кинематика?
4. Что такое система отсчета? Пространство в системе отсчета. Положение точки, отрезка в системе отсчета.
5. Что такое радиус-вектор? Что такое скорость? Мгновенная и средняя.
6. Закон инерции. Что отражает?
7. Какие системы отсчета инерциальные? Принцип относительности Галилея. Какие величины инвариантные?
Задачи
1. Найти зависимость радиус-вектора м.т. от времени и его значение при t 1 = 3 c, если ее скорость меняется со временем по закону (в СИ): 
, а начальные координаты (в метрах) равны (1; 3; 0). R (3) = 15,7 м)
2. Скорость частицы меняется со временем по закону (в СИ): 
. Найти уравнение движения частицы, если в начальный момент она находилась в начале координат. Определить путь, пройденный частицей за время движения 2 с и 5 с. (8 м, 13 м)
3. Автомобиль вторую половину пути шел со скоростью в 1,5 раза большей, чем первую. Его средняя скорость на всем пути 43,2 км/ч. Каковы скорости автомобиля на первой и второй половинах пути?
4. Координаты м.т. (в метрах) следующим образом зависят от времени (в секундах): X = 2 t + 0,5 t 2 – 0,2 t 3, Y = 2, Z = 5. Найти: форму траектории, уравнение движения в векторной форме, вектор скорости, его модуль. Определите значения радиуса вектора, скорости в начальный момент времени и для момента t 1 = 0,5 c.Отв. R (0) = 5,38 м; R = (0,5) = 5,50 м; V (0) = 2 м/с; V (0,5) = 2,35 м/с;
ГЛАВА 2. КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЁРДОГО ТЕЛА: ЛИНЕЙНОЕ УСКОРЕНИЕ, ПОСТУПАТЕЛЬНОЕ
И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ, ЧИСЛО СТЕПЕНЕЙ
СВОБОДЫ, УГЛОВАЯ СКОРОСТЬ, УГЛОВОЕ УСКОРЕНИЕ
1. Что называют линейным (полным) ускорением?
2. Нормальная и тангенциальная составляющие полного ускорения.
3. Какое движение равноускоренное?
4. Как определяются поступательное и вращательное движения? Что такое степени свободы?
5. Угловая скорость и угловое ускорение. Какова их связь с линейной скоростью и ускорением?
Задачи
1. Тело, движущееся равноускоренно, проходит участок пути 60 м за 10 с. При этом скорость на этом участке возрастает в 7 раз. Определить ускорение движущегося тела. Построить график ускорения, скорости и пути, указать на нем рассматриваемый участок.
2. Тело, двигаясь с постоянным ускорением, проходит последовательно два одинаковых отрезка пути по 10 м каждый. Найти ускорение тела и скорость в начале первого отрезка, если первый отрезок пройден за 1,06 с, а второй – за 2,2 с.
3. Автомобиль, двигаясь с постоянной скоростью 25 м/с, промчался мимо милицейского поста, нарушив правила дорожного движения. Спустя 4 с милиционер начал преследование на мотоцикле, двигаясь с постоянным ускорением, и, проехав 780 м, настиг нарушителя. Определить сколько времени для этого потребовалось; ускорение мотоцикла в тот момент, когда он поравнялся с автомобилем.
4. Пункты А и В расположены на расстоянии 4 км друг от друга. Из пункта А по направлению к пункту В выехал автомобиль, который двигался все время равномерно. Одновременно навстречу из пункта В с начальной скоростью 32 м/с выехал автомобиль, движущийся с постоянным ускорением 0,2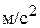 
, направленным все время так же, как скорость первого автомобиля. Известно, что в пути автомобили два раза встречались друг с другом. В каких переделах лежит скорость первого автомобиля?
5. Точка движется в плоскости так, что ее движение описывается уравнениями 
Найти путь, пройденный материальной точкой за 5 секунд; модуль скорости в этот момент времени. Записать уравнение траектории движения материальной точки; уравнения радиус вектора; вектора скорости и вектора ускорения.
6. Угловая скорость тела, вращающегося вокруг неподвижной оси,изменяется со временем по закону:ω (t) = b (1 – e– kt ) (рад/с), где b и k –положительные постоянные. Найдите зависимость от времени угла поворота φ(t) и углового ускорения ε(t), если φ = 0 при t = 0. Для момента времени t = 2 с определить значения φ(2) и ε(2), если b = 2 рад/с и k = 1 с–1. Отв. φ(t) = bt– (b/к)(1– еk t); ε(t)= kbе kt; φ (2) = 4,27 рад; ε(2) = 0,27 рад/с2)
7. Тело одновременно совершает вращения вокруг горизонтальной оси с постоянной угловой скоростью ω1 = 2 рад/с и вокруг вертикальной оси с постоянным угловым ускорением ε2 = 0,5 рад/с. Найдите зависимость угловой скорости и углового ускорения тела от времени. Определите их значения в момент t = 1,4 с от начала движения. Отв. 
; ω(1,4) = 2,1 рад/с;
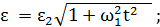ε(1,4) = 1,49 рад/с2
8. Диск радиусом R = 10 см, находящийся в состоянии покоя, начал вращаться с постоянным угловым ускорением = 0,5 рад/с2. Найти тангенциальное, нормальное и полное ускорения точек на ободе диска в конце второй секунды после начала движения. (а = 0,05 м/с2; аn = 0,1 м/с2; аτ = 0,11 м/с2)
9. Колесо вращается вокруг неподвижной оси так, что угол его поворота зависит от времени как 
, где 
. Найти полное линейное ускорение точки на ободе колеса в момент времени 2,5 с, если ее линейная скорость в этот момент 0,65 м/с.
10. Твердое тело вращается с угловой скоростью 
. Найти модули угловой скорости и углового ускорения в момент времени 10 с, а также угол между векторами угловой скорости и углового ускорения в этот момент времени.
Глава 3. КИНЕМАТИКА СПЕЦИАЛЬНОЙ ТЕОРИИ
