Ползучестью называется способность материала деформироваться во времени при действии постоянных нагрузок.
Явление ползучести присуще таким материалам, как бетон, кирпич, полимеры, древесина. Металлы также обнаруживают это свойство деформирования, которое становится особенно заметным при высокой температуре, а в цветных металлах (свинец, медь и др.) даже при комнатной температуре.
Фактор ползучести имеет существенное значение для работы конструкций. Достаточно отметить, что напряжения в арматуре железобетонных конструкций могут в процессе ползучести увеличится в 2-2,5 раза, а перемещения – в 3-4 раза. В машиностроении известны случаи, когда стальные котельные трубы разрушались под действием внутреннего давления вследствие ползучести материала. На рис.12.4 показано разрушение трубы из-за ползучести материала (пунктиром на рисунке нанесены первоначальные и изменяющиеся размеры поперечного сечения трубы).

Рисунок 12.4 – Разрушение трубы из-за ползучести материала
Деформация ползучести  может рассматриватся как очень медленная текучесть маталла. Схематически диаграмму ползучести можно изобразить упрощенной зависимостью
может рассматриватся как очень медленная текучесть маталла. Схематически диаграмму ползучести можно изобразить упрощенной зависимостью  где
где  – время деформирования материала при ползучести (рис. 12.5).
– время деформирования материала при ползучести (рис. 12.5).

Рисунок 12.5 – Диаграмма ползучести
Пренебрегая временем на осуществление упругой деформации  , можно представить возрастание деформаций в виде
, можно представить возрастание деформаций в виде  , где
, где  - деформация ползкчести в условиях ползучести материала:
- деформация ползкчести в условиях ползучести материала:

где  – постоянная скорость ползучести, равная
– постоянная скорость ползучести, равная

α – угол наклона условной линии ползучести (см.рис.12.5).
Условие прочности при ползучести имеет вид:

 – передел ползучести, рассматриваемый как наибольшее напряжение, при котором получаем малую скорость ползучести и пластическую деформацию определенной величины
– передел ползучести, рассматриваемый как наибольшее напряжение, при котором получаем малую скорость ползучести и пластическую деформацию определенной величины  (см. рис. 12.5) за весь срок службы материала при заданной температуре.
(см. рис. 12.5) за весь срок службы материала при заданной температуре.
В задачах расчета деталей машин на ползучесть, кроме проверки условия прочности (12.10), обычно определяется и срок службы детали tg, когда скорость ползучести  не превосходит попускаемую скорость
не превосходит попускаемую скорость  при заданном предельном сроке службы детали
при заданном предельном сроке службы детали  .
.
Вместе с ползучестью деталям свойственно и такое явление, как релаксация. Релаксацией называется уменьшение напряжений в детали в результате постоянного нарастания пластической деформации за счет упругой.
Благодаря релаксации плотность соединения деталей, скрепленных за счет упругого натяга, может быть настолько ослаблена, что вызовет нарушение нормальной работы конструкции. Так, например, ослабление плотности болтового соединения фланцев газопровода или цилиндров высокого давления паровой турбины может привести к утечке газа или пара, если не проводить периодические ремонтные работ фланцевого соединения. Таким образом, с явлением релаксации необходимо считаться в процессе эксплуатации машин и механизмов.
При релаксации имеет место процесс постепенного снижения напряжений в нагруженной детали, полная деформация которой не может изменятся во времени и равна полученной при нагружении упругой деформации. При этом снижение напряжений происходит вследствие постепенного уменьшения упругой деформации и приращения на ту же величину пластической деформации на основании зависимостей:


где  – изменение длины детали соответственно в упругой и пластических областях при деформации
– изменение длины детали соответственно в упругой и пластических областях при деформации  ;
;  – первоначальное напряжение в детали;
– первоначальное напряжение в детали;  – модуль упругости материала при заданной температуре.
– модуль упругости материала при заданной температуре.
Дифференциальную вторую зависимость (12.11) по времени t и заменяя  на
на  получаем дифференциальное уровнение, решение которого дает функциональную зависимость напряжения в детали от времени при релаксации
получаем дифференциальное уровнение, решение которого дает функциональную зависимость напряжения в детали от времени при релаксации  ), где
), где 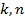 – опытные коэффициенты, зависящие от свойств материала и температуры эксплуатации.
– опытные коэффициенты, зависящие от свойств материала и температуры эксплуатации.
Основные понятия о расчете элементов конструкций в области пластических деформаций
12.4.1. Расчет элементов конструкции по несущей способности
До сих пор в проведенных расчетах прочности элементов конструкций в упругой области при статическом нагружении рассматривался метод допускаемы напряжений. По этому методу условия прочности элемента конструкции считались нарушенными, если хотя бы в одной точке этого элемента напряжение достигало опасной величины – допускаемого напряжения (такой подход именуется еще расчетом по опасной точке).
Для расчета конструкций из пластичных материалов типа стали при статическом наружении возможен и другой подход к оценке их прочности – расчет по методу продольного состояния, или несущей способности. При этом считается, что достижение предела текучести в одной точке (точках) не приводит к выходу из строя всей конструкции и ее состояние не считается предельным. Несущая способность конструкции будет исчерпана, когда она обратится в геометрически изменяемую систему при неограниченном деформировании при постоянной нагрузке. Такая нагрузка (сила или момент) считается предельной нагрузкой, а состояние конструкции именуется предельным и соответствует исчерпанию ее несущей способности.
Расчет прочности элементов конструкции или ее в целом при таком условии называется расчетом по предельному состоянию, или расчетом по несущей способности. Такой подход является более простым в расчете по учету пластических деформаций, которые могут возникнуть в конструкции и их элементах.
Условие прочности по предельному состоянию (нагрузке) записывается в виде:

где  – предельное значение нагрузки (силы или момента), при котором несущая способность конструкции будет исчерпана;
– предельное значение нагрузки (силы или момента), при котором несущая способность конструкции будет исчерпана;
 – действующая нагрузка на кострукцию;
– действующая нагрузка на кострукцию;
 – действительный коэффициент запаса прочности;
– действительный коэффициент запаса прочности;
 – требуемый (заданный) коэффициент запаса прочности.
– требуемый (заданный) коэффициент запаса прочности.
Часто расчеты по несущей способности базируются на том, что материал конструкции является идеально упругопластичным. Схематизированная диаграмма деформирования такого материала определяется упрощенной диаграммой растяжения (рис.12.6). Обычно предполагается, что диаграмма сжатия такая же (в пределах относительно малых пластических деформаций), как и при растяжении.

Рисунок 12.6 – Схематизированная диаграмма растяжения материала
Диаграмма состоит из двух прямолинейных участков ОА и АВ (см. рис. 12.6).
Участок ОА соответствует упругой деформации материала, где соблюдается закон Гука. Предполагается, что крайнее значение участка – предел пропорциональности материала – равны пределам текучести, т.е. 
Второй участок диаграммы АВ соответствует состоянию текучести материала, причем считается, что площадка текучести имеет неограниченную протяженность.
Применение такой схематизированной диаграммы «напряжения σ(τ) – деформации  ′′ (она называется диаграммой Прандля) существенно упрощает расчеты по несущей способности.
′′ (она называется диаграммой Прандля) существенно упрощает расчеты по несущей способности.
В статически определимых системах, элементы которых работают на растяжение и сжатие, результаты расчета по несущей способности совпадают с результаты расчета по опасной точке. Действительно, нагрузка текучести возникает во всех точках наиболее напряженного элемента конструкции и переход в состояние текучести всех элементов превращает систему в геометрически изменяемую.
В статически неопределимой системе, элементы которой в упругой стадии работы нагружены различно, возникновение текучести в каком-либо элементе не приводит к исчерпанию несущей способности всей системы, так как остальные элементы системы находятся в упругой стадии и еще не способны оказывать сопротивление возрастающей нагрузке. В этих случаях предельная нагрузка  будет больше
будет больше  , при котрой текучесть возникает лищь в одном элементе. Отсюда следует, что допускаемая нагрузка для статически неопределимой системы, рассчитанной по несущей способности, будет больше, чем в случае расчета этой системы по опасной точке при одинаковых коэффициентах запаса прочности.
, при котрой текучесть возникает лищь в одном элементе. Отсюда следует, что допускаемая нагрузка для статически неопределимой системы, рассчитанной по несущей способности, будет больше, чем в случае расчета этой системы по опасной точке при одинаковых коэффициентах запаса прочности.
В общем случае, коэффициенты запаса при расчете по несущей способности будут выше, чем при по расчете по опасной точке.
Когда в упругой стадии работы системы напряжения в поперечных сечениях ее элементов распределены неравномерно (например, при кручении или изгибе), расчет по несущей способности дает результат, отличный от расчета по опасной точке, даже если система статические определима.
12.4.2. Расчет несущей способности бруса на растяжение (сжатие)
Пример 12.1. Определить по расчету несущей способности допускаемую величину силы Р для статически неопределимого бруса (рис. 12.7). Материал бруса Ст.3 с пределом текучести  требуемый коэффициент запаса прочности
требуемый коэффициент запаса прочности 

Рисунок 12.7 – К расчету несущей способности бруса
Решение
Обозначив реакции в защемлении концов бруса  и
и  , составим уравнение равновесия:
, составим уравнение равновесия:

Из условия нагружения бруса силой Р (см. рис. 12.7) видно, что верхняя часть бруса от места приложения силы испытывает растяжение с растягивающим усилием  , а нижняя часть – сжатие при сжимающем усилии
, а нижняя часть – сжатие при сжимающем усилии  .
.
В предельном состоянии конструкции напряжения в обеих частях бруса достигают предела текучести  и отсюда реакции равны:
и отсюда реакции равны:

где F – площадь поперечного сечения бруса.
Подставляя значения реакций (12.4) в уравнение (12.13) и учитывая, что в предельном состоянии усилие Р достигает своего предельного значения, имеем:

или

откуда

Учитывая коэффициент запаса прочности  допускаемая нагрузка равна:
допускаемая нагрузка равна:

12.4.3. Расчет несущей способности балок при поперечном изгибе
В расчет на изгиб балки из пластичного материала по методу допускаемых напряжений опасным считается то состояние балки, при котором в опасном сечении по ее длине в крайних его точках А, В максимальные напряжения достигают предела текучести материала (рис. 12.8, б).
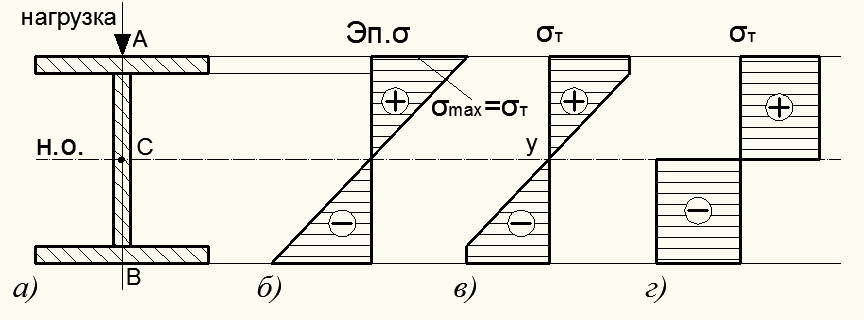
Рисунок 12.8 – Эпюры нормальных напряжений балки при изгибе
По мере возрастания нагрузки, а значит величины изгибающего момента в опасном сечении балки, текучесть будет охватывать все большую площадь сечения: одна его часть будет работать упруго, а другая часть – охвачена пластическими деформациями при напряжениях  (рис. 12.8, в). Наконец, текучестью будет охвачена вся площадь сечения балки (рис. 12.8, г). Это соответствует случаю, когда несущая способность балки будет исчерпана.
(рис. 12.8, в). Наконец, текучестью будет охвачена вся площадь сечения балки (рис. 12.8, г). Это соответствует случаю, когда несущая способность балки будет исчерпана.
Возникновение полной текучести в опасном поперечном сечении можно уподобить образованию в этом сечении так называемого пластического шарнира (рис. 12.9), который превращает балку в геометрически измененную систему и ее части раздельно поворачиваются в шарнире друг относительно друга. При этом поперечная нагрузка будет соответствовать своему предельному значению  .
.
Величина изгибающего момента балки в месте шарнира называется предельным изгибающим моментом 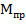 (см.рис.12.9), равным
(см.рис.12.9), равным

где  – предельный (пластический) момент сопротивления сечения балки.
– предельный (пластический) момент сопротивления сечения балки.

Рисунок 12.9 – Возникновение пластического шарнира балки в предельном состоянии
При симметричном относительно н.о. сечении балки (см. рис. 12.8) величина  равна:
равна:
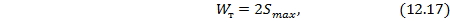
где  - статический момент половины сечения балки относительно н.о.
- статический момент половины сечения балки относительно н.о.
Например, для прямоугольного поперечного сечения балки (рис.12.10) предельный момент сопротивления будет:


Рисунок 12.10 – К вычислению  для прямоугольного сечения
для прямоугольного сечения
При несимметричном поперечном сечении балки относительно н.о. (рис. 12.11) охват текучестью всего сечения делит его на две равновеликие части  и предельный момент сопротивления определяется по формуле:
и предельный момент сопротивления определяется по формуле:
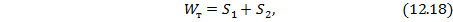
где  – статические моменты (
– статические моменты ( ) сечений балки
) сечений балки  относительно н.о. (учитываются по абсолютной величине).
относительно н.о. (учитываются по абсолютной величине).

Рисунок 12.11 – К вычислению  для несимметричного сечения
для несимметричного сечения
Предельный изгибающий момент для этого сечения рассчитывается по формуле (12.16).
Изгибающий момент для балки, при котором максимальные напряжения в наиболее удаленных от н.о. точках сечения равны пределу текучести материала, равен:

где  – момент сопротивления сечения балки относительно его крайней точки.
– момент сопротивления сечения балки относительно его крайней точки.
Этот момент считается опасным с позиции расчета балки по допускаемым напряжениям (опасной точки).
Из приведенных формул (12.16) и (12.19) имеет место соотношение 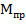 к
к  или
или  к
к  :
:

Величина этого отношения определяется формой поперечного сечения балки. Так, для балки прямоугольного поперечного сечения  а для прокатного симметричного двутавра
а для прокатного симметричного двутавра 
 Пример 12.2. Определить допускаемую величину интенсивности распределенной нагрузки для двухопорной стальной балки (рис. 12.12, а), поперечное сечение которой изображено на рис. 12.12, б. Предел текучести материала
Пример 12.2. Определить допускаемую величину интенсивности распределенной нагрузки для двухопорной стальной балки (рис. 12.12, а), поперечное сечение которой изображено на рис. 12.12, б. Предел текучести материала  требуемый коэффициент запаса
требуемый коэффициент запаса 
Рисунок 12.12 – К расчету несущей способности изгибаемой балки
Решение
1. Находим положение н.о. поперечного сечения балки из условия того, что в предельном состоянии н.о. делит сечение на две равновеликие части (см.рис.12.12):

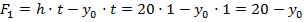

Подставляем полученные выражения в условие (12.21) и определяем положение н.о. сечения балки в предельном состоянии:

2. Рассчитываем статические моменты полусечений балки относительно н.о.:


3. Предельный момент сопротивления сечения равен:

4. Предельный изгибающий момент для балки:

5. Рассчитываем допускаемый изгибающий момент балки в предельном состоянии:

6. Наибольший изгибающий момент посредине пролета балки от заданной внешней нагрузки (см. рис.12.12,а) выражается формулой:

7. Считается, что внешняя нагрузка в формуле (12.23) равна допускаемой 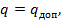 приравниваем значения
приравниваем значения  и
и 

откуда

Задание для индивидуальной работы
Рассчитать допустимую длину  двухопорной балки (рис.12.13, а), которая загружена в пролете сосредоточенной силой
двухопорной балки (рис.12.13, а), которая загружена в пролете сосредоточенной силой  . Балка прямоугольного поперечного сечения
. Балка прямоугольного поперечного сечения 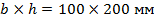 (рис. 12.13, б), материал балки – Ст.3 с пределом текучести
(рис. 12.13, б), материал балки – Ст.3 с пределом текучести  требуемый коэффициент запаса
требуемый коэффициент запаса 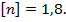

Рисунок 12.13
Тести з опору матеріалів
1. Що вивчає наука “Опір матеріалів”?
а) теорію машин і механізмів;
б) основи надійності деталей машин;
в) основи розрахунків на міцність, жорсткість і стійкість елементів конструкцій.
2. Вчені, що зробили значний внесок у розвиток науки з опору матеріалів:
а) Архімед;
б) Галілео Галілей;
в) Ньютон;
г) Р.Гук;
д) С.П. Тімошенко.
3. Які тіла розглядаються в опорі матеріалів у відмінності від теоретичної механіки?
а) абсолютно тверді тіла;
б) деформовані тверді тіла;
4. На яких властивостях матеріалу побудовані основні розрахункові схеми елементів конструкцій в опорі матеріалів?
а) пружності;
б) пластичності;
в) в’язкості;
5. Пояснити поняття міцності елементів конструкцій:
а) мати прогини при навантаженні не більш допустимих;
б) зберігати прямолінійну форму при стисканні;
в) не підлягати руйнації при дії зовнішніх сил
6. Пояснити поняття жорсткості елементів конструкцій:
а) не підлягати руйнації при дії зовнішніх сил;
б) мати прогини при навантаженні не більш допустимих;
в) зберігати прямолінійну форму при стисканні.
7. Пояснити поняття стійкості елементів конструкцій:
а) мати прогини при навантаженні не більш допустимих;
б) не підлягати руйнації при дії зовнішніх сил;
в) зберігати прямолінійну форму при стисканні.
8. Що називається пружністю деформованих тіл?
а) властивістю зберігати деформацію після дії зовнішніх сил;
б) властивістю усувати деформацію після дії зовнішніх сил.
9. Які гіпотези про деформованість тіл приймаються в опорі матеріалів?
а) пружності матеріалу;
б) суцільності;
в) плоских перерізів.
10. Які допущення про деформованість тіл приймаються в опорі матеріалів?
а) лінійності;
б) однорідності;
в) ізотропності;
г) принципи Сен-Венана, незалежності дії сил;
д) суцільності.
11. Види пружних тіл, які розглядаються в опорі матеріалів:
а) масив;
б) брус;
в) стержень;
г) балка;
д) пластина;
ж) оболонка.
12. Які види деформацій розглядаються в опорі матеріалів?
а) повздовжня деформація при розтягненні-стисканні брусу;
б) зріз і зм’яття з’єднувальних елементів;
в) закручування;
г) вигин;
д) руйнація.
13. Що називається деформацією в точці тіла?
а) збільшення або зменшення довжини волокна тіла;
б) відношення зміни довжини волокна тіла до його первинної довжини;
в) границя відношення зміни довжини волокна тіла до його первинної довжини.
14. Які розрізняють види деформацій в точці тіла:
а) лінійні;
б) кутові;
в) об’ємні;
15. Які види зовнішніх сил (навантажень) розглядаються в опорі матеріалів?
а) зосереджувальна сила Р  ;
;
б) повздовжнє зусилля N, згинальний момент М, зрізуюча сила Q в розрахунках напружень;
в) інтенсивність сил.
г) зосереджу вальний момент ɱ, який прикладений до конструкцій.
д) реактивний згинальний момент, зрізуючи сила.
16. Яка послідовність розрахунку міцності брусу при розтягненні (стисканні)?
а) розрахунок нормальних напружень в поперечних перерізах брусу  , змін довжини частин брусу
, змін довжини частин брусу  , повздовжних внутрішніх зусиль N;
, повздовжних внутрішніх зусиль N;
б) розрахунок змін довжини частин брусу  ,нормальних напружень в поперечних перерізах
,нормальних напружень в поперечних перерізах  , повздовжних внутрішніх зусиль N;
, повздовжних внутрішніх зусиль N;
в) розрахунок повздовжних внутрішніх зусиль N, нормальних напружень в поперечних перерізах  , змін довжини частин брусу
, змін довжини частин брусу  .
.
17. Як розраховуються геометричні характеристики поперечних перерізів елементів конструкцій?
а) об’єм елемента конструкцій; б) площа поперечного перерізу елемента;
в) довжина елемента;
г) статичні моменти частин перерізу;
д) центр тяжіння площі поперечного перерізу;
ж) моменти інерцій частин перерізу.
18. Для чого необхідно мати геометричні характеристики перерізів елементів конструкцій?
а) для розрахунку деформації елементів;
б) для розрахунку напружень в поперечних перерізах;
в) для розрахунку жорсткості елементів конструкцій.
19. Як розраховуються статичний момент частини поперечного перерізу елемента конструкції відносно горизонтальної осі порівняння z:
а)  ; б)
; б) 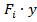 ; в)
; в)  ; г) немає правильної відповіді.
; г) немає правильної відповіді.
20. Як розраховується осьовий момент інерції частини поперечного перерізу елемента конструкції відносно горизонтальної осі z:
а)  ; б)
; б) 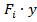 ; в)
; в)  ;
;
21. Як розраховується полярний момент інерції поперечного перерізу елемента конструкції?
 ; б)
; б) 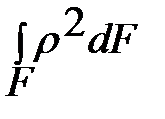 ; в)
; в)  ; г) немає правильної відповіді.
; г) немає правильної відповіді.
22. Яка ось відносно поперечного перерізу елемента конструкції називається центральною?
а) яка розміщена довільно відносно площі поперечного перерізу;
б) яка проходить через центр тяжіння площі поперечного перерізу;
в) яка повернута на кут  відносно осі порівняння;
відносно осі порівняння;
г) паралельна осі, що проходить через центр тяжіння поперечного перерізу.
а); б); в); г); б, г).
23. Розглядається площа F довільної плоскої фігури у двох осях координат: горизонтальної осі z та вертикальної осі y, що проходять через центр тяжіння фігури центральні осі; інші осі  які розташовані паралельно центральним осям. За якою формулою розраховується один з центральних моментів інерції, якщо паралельні осі z та
які розташовані паралельно центральним осям. За якою формулою розраховується один з центральних моментів інерції, якщо паралельні осі z та  розміщена одна від одної на відстані а:
розміщена одна від одної на відстані а:
а)  б)
б)  в) немає правильної відповіді.
в) немає правильної відповіді.
24. Напруження в точці тіла це:
а) міра інтенсивності внутрішніх зусиль;
б) зовнішня сила, яка припадає на одиницю площі;
в) границя відношення елементарної сили до елементарної площини.
а); б); в); немає правильної відповіді.
25. Які види напружень розглядаються в опорі матеріалів?
а) октаедричні;
б) лінійні;
в) нормальні;
г) дотичні.
а); б); в); г); в), г).
26. Для чого використовується метод перерізів розглядаємих елементів?
а) для розрахунку внутрішніх зусиль;
б) для розрахунку деформацій;
в) для розрахунку видовжень або скорочень розглядаємих елементів конструкцій при зовнішньому навантаженні.
а); б); в).
27. За якою формулою розраховуються нормальні напруження в перерізах при розтягуванні (стисканні) брусу?
а)  ; б)
; б)  ; в)
; в) 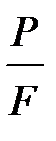 ; г) немає правильної відповіді.
; г) немає правильної відповіді.
28. Закон Гука при розтягуванні (стисканні) брусу:
а)  ; б)
; б)  ; в) немає правильної відповіді.
; в) немає правильної відповіді.
29. Від яких напружень виникає деформація зсуву?
а) нормальних напружень  ;
;
б) дотичних напружень  .
.
30. Закон Гука при деформації зсуву:
а)  ; б)
; б)  ; в) немає правильної відповіді.
; в) немає правильної відповіді.
31. Від яких напружень виникає деформація зм’яття?
а) нормальних напружень  ;
;
б) дотичних напружень  .
.
а); б).
32. В яких випадках виникають деформації зсуву та зм’яття?
а) при розтягуванні (стисканні) брусу;
б) при розтягуванні заклепочних, шпоночних, болтових з’єднань листів;
в) при розтягуванні зварювальних з’єднань у флангових; лобових швах.
а); б); б), в).
33. За якою формулою (1) і за яких напружень (2) розраховуються міцність на зсув заклепальних з’єднань?
1, а)  ; 1, б)
; 1, б)  ; 2,а) нормальних; 2,б) дотичних.
; 2,а) нормальних; 2,б) дотичних.
34. За якою формулою (1) і за яких напружень (2) розраховуються міцність на змя’ття заклепальних з’єднань з і заклепками?
1, а)  ; 1, б)
; 1, б)  ; 2,а) нормальних; 2,б) дотичних.
; 2,а) нормальних; 2,б) дотичних.
35. Закручуванням називається такий вид деформацій від напружень (1), коли в поперечних перерізах діє тільки внутрішні зусилля (2):
1, а) нормальних; 1, б) дотичних; 2, а) момент зкручування; 2, б)згинальний момент.
36. За якими формулами оцінюється міцність вала за деформацією закручування?
а)  ; б)
; б)  ; в)
; в)  ; г) немає правильної відповіді.
; г) немає правильної відповіді.
37. Які характеристики розраховуються при закручуванні вала?
а) нормальні напруження; б) дотичні напруження; в) кут закручування.
38. Що визначається в розрахунках міцності при закручуванні вала?
а) дотичні напруження в перерізах вала;
б) кути закручування;
в) діаметр вала;
г) довжина вала.
39. За якою формулою розраховуються кути закручування вала при його подальшій експлуатації?
а) 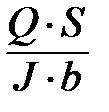 ; б)
; б)  ; в)
; в)  .
.
40. Для чого необхідно визначати механічні характеристики матеріалу?
а) для вибору матеріалу деталі, конструкції;
б) для розрахунків міцності елементів конструкції;
в) для визначення об’єму виробництва підприємства.
а); б); а), б), в); г) немає правильної відповіді.
41. За якими видами розрізняють механічні випробування матеріалів?
а) за обсягом робіт;
б) за характером випробувань;
в) за видом деформації.
а), б), в).
42. Які механічні характеристики матеріала визначають при статичних випробуваннях при розтягненні зразків на пресі:
а) характерні напруження матеріалу;
б) характеристики пластичності матеріалу;
в) ударна в’язкість;
г) твердість.
а); б); в); г); а), б); б), в).
43. З якою метою визначають допустимі напруження в розрахунках опору матеріалів?
а) для оцінки стійкості елемента конструкції;
б) для оцінки жорсткості елемента конструкції;
в) для оцінки міцності елемента конструкції.
а); б); в).
44) За яких напружень обчислюються їх допустима величина?
а) напруження пружності;
б) напруження пропорціональності;
в) напруження плинності;
г) границя міцності.
а); б); в); г).
45. Які види згину балок розглядаються в опорі матеріалів?
а) змішаний;
б) об’ємний;
в) чистий;
г) поперечний;
д) косий.
а); б); в); г); д).
46.Що приймається за пружну лінію балки?
а) верхні волокна балки;
б) нижні волокна;
в) геометричне місце центрів тяжіння поперечних перерізів при згинанні балки.
а); б); в).
47. На шарнірних опорах балки відсутні:
а) вертикальні переміщення опорних перерізів;
б) кути повороту опорних перерізів.
а); б); а),б).
48. На жорсткому закріпленні кінця балки відсутні:
а) переміщення опорних перерізів;
б) кути повороту опорних перерізів.
а); б); а),б).
49. У статично визначених балках для розрахунку реакцій умов статики:
а) достатньо;
б) недостатньо.
50. Які умови статики використовуються для розрахунку реакцій при поперечному згинанні балки:
а) сума усіх сил на вертикальну ось дорівнює нулю;
б) сума моментів усіх силових факторів відносно довільної точки за довжиною балки дорівнює нулю;
в) сума моментів усіх силових факторів відносно опор балки дорівнює нулю.
а), б); а), в); а), б) в).
51. Як внутрішні силові фактори розраховуються при згинанні балок:
а) температурне поле;
б) зрізуюча сила;
в) згинальний момент.
а); б), в); а),б), в).
52. Зрізуюча сила Q в перерізі балки є рівнодіючою:
а) нормальних напружень;
б) дотичних напружень;
в) зовнішніх сил і моментів.
а); б); в).
53. До згинального моменту М в перерізі балки приводять:
а) нормальні напруження;
б) дотичні напруження;
в) зовнішні сили і моменти.
а); б); а), в).
54. Правило знаків для зрізуючої сили Q при побудові епюри Q, прийняте в опорі матеріалів:
а) додатна, якщо для її визначення розглядаємі зовнішні сили зорієнтовані вверх для лівої частини балки від проведеного перерізу;
б) додатна, якщо для її визначення розглядаємі зовнішні сили направлені вниз для правої частини балки від проведеного перерізу;
в) невід’ємна, якщо для лівої частини балки зовнішні сили направлені вверх і вниз для правої частини балки.
а); б); в).
55. Правило знаків для згинального моменту М при побудові епюри М, прийняте в опорі матеріалів:
а) додатний, якщо він визиває стиснення верхніх волокон балки при її прогині випуклістю вниз від розглядаємого перерізу;
б) додатний, якщо він визиває розтягнення верхніх волокон балки від розглядає мого перерізу.
а); б).
56. Що пов’язують між собою диференційні залежності між факторами згинання балки:
а) зовнішнє навантаження зі згинальним моментом у перерізі балки;
б) зрізуючі сили і згинальні моменти;
в) інтенсивність поперечного навантаження зі зрізуючою силою і згинальним моментом в перерізі балки.
а); б); б), в); а), б), в).
57. За якою формулою розраховуються нормальні напруження  в поперечних перерізах при згинанні балки:
в поперечних перерізах при згинанні балки:
а)  ; б)
; б)  ; в)
; в)  .
.
а); б); в); г) відповіді є неправильними.
58. В яких точках за висотою поперечного перерізу балки виникають максимальні нормальні напруження  :
:
а) у центрі тяжіння (ц.т.) перерізу балки;
б) у найбільш віддалених точках від ц.т.;
в) в точках змикання стінки з поясками балки составного профілю.
а); б); в); г) усі відповіді є неправильні.
59. В яких точках за висотою поперечного перерізу балки виникають максимальні дотичні напруження  :
:
а) у центрі тяжіння (ц.т.) перерізу балки;
б) у найбільш віддалених точках від ц.т.;
в) в точках змикання стінки з поясками балки составного профілю.
а); б); в); г) усі відповіді є неправильні.
60. За яким законом (показати на рисунку) розподіляються нормальні напруження  за висотою поперечного перерізу балки:
за висотою поперечного перерізу балки:
а) за законом квадратичної параболи;
б) за лінійним законом.
а); б); в) усі відповіді є неправильні.
61. За яким законом (показати на рисунку) розподіляються дотичні напруження  за висотою поперечного перерізу балки:
за висотою поперечного перерізу балки:
а) за законом квадратичної параболи;
б) за лінійним законом.
а); б); в) усі відповіді є неправильні.
62. Які елементи вигину балок відносяться до кінематичних?
а) прогини за довжиною балки;
б) кути повороту поперечних перерізів.
63. Яке з диференціальних рівнянь характеризує пружну лінію балки при її вигині? Пояснити величини в рівнянні
а) Е І w  = q;
= q;
б) Е І w  = М.
= М.
64. Які методи використовуються для розрахунку переміщень балок за їх довжиною?
а) метод інтегрування диференціального рівняння пружної лінії;
б) метод початкових параметрів;
в) енергетичні методи.
65. З яких умов визначаються постійні інтегрування диференціального рівняння пружної лінії балки?
а) за видом зовнішнього навантаження;
б) за умов допустимих переміщень;
в) з граничних умов на опорах.
66. Які недоліки має метод визначення переміщень балки при інтегруванні диференційного рівняння пружної лінії?
а) працездатність розрахунків;
б) необхідність визначення постійних інтегрування на кожній межі навантаження.
67. Які переваги має метод початкових параметрів у визначеності переміщень балок?
а) наявність одного універсального рівняння для визначення переміщень балки;
б) необхідність розрахунку лише чотирьох початкових параметрів за будь-якої кількості меж навантаження балки.
68. Якщо розподілене навантаження не доходить до правої кінцевої межі балки, то необхідно:
а) використати без зміни навантаження універсальне рівняння для переміщень;
б) уявно продовжити до правого кінця балки розподілене навантаження з урахуванням навантаження зворотнього напрямку.
69. Які з енергетичних методів використовуються у розрахунках переміщень балок?
а) Лагранжа, Клапейрона;
б) Кастільяно, Мора;
в) Верещагіна.
70. За якою формулою розраховується потенційна енергія пружної деформації балки?
а) V = P ·l, де P – узагальнена сила; ·l – довжина балки;
б) V =  , де P – узагальнена сила;
, де P – узагальнена сила;  - узагальнене переміщення.
- узагальнене переміщення.
71. Що розуміють під поняттям “узагальнене переміщення” в енергетичних методах для балки?
а) прогин;
б) кут повороту поперечного перерізу.
72. Що розуміють під поняттям “узагальнена сила” в енергетичних методах для балки?
а) зосереджувальна сила;
б) зрізуючи сила;
в) згинальний момент.
73. Якщо необхідно визначити прогин балки в перерізі, де не прикладена зосереджувальна сила, то в енергетичних методах необхідно:
а) уявно прикласти в перерізі балки додатковий згинальний момент М д який в кінці розрахунків покласти М д = 0;
б) уявно прикласти в перерізі балки додаткову зосереджувальну силу, а в кінці розрахунків покласти Р д = 0.
74. Якщо необхідно визначити кут повороту переріза балки, де не прикладений згинальний момент в енергетичних методах, то необхідно:
а) уявно прикласти в перерізі балки додаткову зосереджу вальну силу Р д , яку в кінці розрахунків покласти Рд = 0;
б) уявно прикласти в перерізі балки додатковий згинальний момент М д , який в кінці розрахунків покласти М д = 0.
75. Записати формулу для визначення прогину балки за теоремою Кастільяно.
76. Записати формулу для визначення кута повороту поперечного переріза балки за теоремою Кастільяно.
77. Записати формулу для визначення прогину балки за інтегралом Мора.
78.Записати формулу для визначення кута повороту поперечного переріза балки за інтегралом Мора.
79. Записати узагальнену формулу для визначення переміщень балки за способом Верещагіна.
80. Для статично невизначених однопрогонних балок рівнянь статики достатньо для розрахунку елементів вигину?
а) достатньо;
б) не достатньо.
81. Який метод розрахунку елементів вигину використовується для багатопрогонних балок на жорстких шарнірних опорах? В чому його сутність.
82. Що входить в поняття “складний опір?”
а) косий згин балки;
б) згин балки від сумісного поперечного і продольного навантаження;
в) сумісна дія згину і закручування вала.
83. Що розуміють під поняттям “косий згин” для балки?
а) коли при згині балки зовнішнє навантаження діє в одній з площин головних осей інерцій;
б) коли площина дії зовнішніх сил не співпадає з площинами, які проходять через головні осі інерції.
84. Ким з видатних вчених була вперше вирішена задача про стійкість шарнірно опертої балки?
а) Архімедом;
б) Галілеєм;
в) Ейлером.
85. Якій області роботи балки відповідає формула для ейлеревої сили:
а) пружній області;
б) області пружно-пластичних деформацій.
86. Записати формулу для ейлеревої сили Ре при загальному випадку закріплення кінців однопрогонної балки.
87. Коли виникає необхідність в розрахунку критичної сили при стисканні одно прогонної балки?
а) при втраті стійкості в пружній області;
б) при втраті стійкості в області пружно-пластичних деформацій.
88. Що означає втрата стійкості балки?
а) порушення міцності балки;
б) виникнення для первинно прямолінійної балки вигину при стисканні.
89. Які підходи використовуються у розрахунковій практиці при визначенні критичних напружень для балки?
а) графік акад. Ю.А. Шиманського (показати на рисунку);
б) формула проф. Р.С. Ясинського (навести формулу з поясненнями).
СПИСОК ЛИТЕРАТУРЫ
1. Беляев Н.М. Сопротивление материалов  : Учебник / Н.М. Беляев, 15-е издание перераб. и доп. – М.: Наука, 1976. – 608 с.
: Учебник / Н.М. Беляев, 15-е издание перераб. и доп. – М.: Наука, 1976. – 608 с.
2. Беляев Н.М. Сборник задач по сопротивлению материалов  / Н.М. Беляев. – М.: Наука, 1965. – 348 с.
/ Н.М. Беляев. – М.: Наука, 1965. – 348 с.
3. Бурдун Е.Т. Сборник вопросов и задач по сопротивлению материалов для самостоятельной работы студентов  / Е.Т. Бурдун, А.В. Жижко. – Николаев: НКИ, 1993. – 34 с.
/ Е.Т. Бурдун, А.В. Жижко. – Николаев: НКИ, 1993. – 34 с.
4. Дарков А.В. Сопротивление материалов  : Учебник / А.В. Дарков, Г.С. Шпиро, 5-е издание перераб. и доп. – М:Высшая школа, 1989. – 634 с.
: Учебник / А.В. Дарков, Г.С. Шпиро, 5-е издание перераб. и доп. – М:Высшая школа, 1989. – 634 с.
5. Кинасишвили Р.С. Сопротивление материалов  : Учебник / Р.С.Кинасишвили. – М.:Наука, 1975. – 384 с.
: Учебник / Р.С.Кинасишвили. – М.:Наука, 1975. – 384 с.
6. Корнілов В.К. Опір матеріалів  : Методичні вказівки / В.К. Корнілов. – Миколаїв: УДМТУ, 2003. – 100 с.
: Методичні вказівки / В.К. Корнілов. – Миколаїв: УДМТУ, 2003. – 100 с.
7. Корнилов В.К. Краткий курс сопротивления материалов  : Учеб. пособие / В.К. Корнилов. – Херсон: Типография «СТАР», 2004. – 148 с.
: Учеб. пособие / В.К. Корнилов. – Херсон: Типография «СТАР», 2004. – 148 с.
8. Кржечковский П.Г. Методические указания к выполнению расчетных работ по сопротивлению материалов  / П.Г. Кржечковский. – Николаев: НКИ, 1987. – 44 с.
/ П.Г. Кржечковский. – Николаев: НКИ, 1987. – 44 с.
9. Лапин В.Г. Пособие для самостоятельной работы студентов при изучении курса сопротивления материалов  / В.Г. Лапин. – Николаев: НКИ, 1990. – 83 с.
/ В.Г. Лапин. – Николаев: НКИ, 1990. – 83 с.
10. Лугінін О.Є. Тести з дисципліни «Опір матеріалів» з напрямів підготовки «Машинобудування», «Зварювання», «Суднобудування та океанотехніка». Частини 1,2  / О.Є. Лугінін. – Херсон: ХФ НУК, 2014. Частина 1 – 12 с. Частина 2 – 8 с.
/ О.Є. Лугінін. – Херсон: ХФ НУК, 2014. Частина 1 – 12 с. Частина 2 – 8 с.
11. Лугінін О.Є. Комплексні контрольні роботи з дисципліни «Опір матеріалів» для студентів з напрямів підготовки «Суднобудування та океанотехніка», «Зварювання», «Машинобудування»  / О.Є. Лугінін. – Херсон: ХФ НУК, 2014. – 8 с.
/ О.Є. Лугінін. – Херсон: ХФ НУК, 2014. – 8 с.
12. Миролюбов И.Н. Пособие к решению задач по сопротивлению материалов  / И.Н. Миролюбов, С.А. Енгалычев, Н.Д. Сергиевский, 5-е издание перераб. и доп. – М.: Высшая школа, 1985. – 399 с.
/ И.Н. Миролюбов, С.А. Енгалычев, Н.Д. Сергиевский, 5-е издание перераб. и доп. – М.: Высшая школа, 1985. – 399 с.
13. Неженцев П.І. Розрахунково-графічні завдання за курсом «Опір матеріалів»  : Навч. посібник. – Миколаїв: МКІ, 1979. – 46 с.
: Навч. посібник. – Миколаїв: МКІ, 1979. – 46 с.
14. Ободовський Б.А. Сопротивление материалов в примерах и задачах  : Учеб. пособие / Б.А. Ободовский, С.Е. Ханин, 2-е издание исправл. и доп. – Харьков: ХГУ, 1968. – 384 с.
: Учеб. пособие / Б.А. Ободовский, С.Е. Ханин, 2-е издание исправл. и доп. – Харьков: ХГУ, 1968. – 384 с.
15. Писаренко Г.С. Опір матеріалів  : Підручник / Г.С. Писаренко, О.Л.Квітка, Е.С. Уманський. – К.: Вища школа, 1997. – 675 с.
: Підручник / Г.С. Писаренко, О.Л.Квітка, Е.С. Уманський. – К.: Вища школа, 1997. – 675 с.
16. Писаренко Г.С. Сопротивление материалов  : Учебник / Г.С. Писаренко, А.Л. Квитка, Е.С. Уманский. – К.: Вища школа, 1986. – 775 с.
: Учебник / Г.С. Писаренко, А.Л. Квитка, Е.С. Уманский. – К.: Вища школа, 1986. – 775 с.
17. Спіхтаренко В.В. Конспект лекцій з опору матеріалів у 2-х частинах  / В.В. Спіхтаренко. – Херсон: ХФ НУК, 2011. – Частина 1 – 32с. Частина 2 - 38с.
/ В.В. Спіхтаренко. – Херсон: ХФ НУК, 2011. – Частина 1 – 32с. Частина 2 - 38с.
18. Феодосьев Б.И. Сопротивление материалов  : Учебник / Б.И. Федосьев. – М.: Наука, 1974. – 560 с.
: Учебник / Б.И. Федосьев. – М.: Наука, 1974. – 560 с.
19. Фесик С.П. Справочник по сопротивлению материалов  / С.П. Фесик. – К.: Будівельник, 1970. – 308 с.
/ С.П. Фесик. – К.: Будівельник, 1970. – 308 с.
Навчальне видання
Лугінін Олег Євгенович, д-р філософі, професор
Дудченко Олег Миколайович, к.т.н., доцент
Навчально-методичний посібник
з опору матеріалів для самостійної
та індивідуальної роботи студентів
Видавництво ТОВ «Борисфен»
м. Херсон, вул. 9 січня,15,
т/ф (0552) 42-02-19, 26-29-73
e-mail: borisfen-pro@ukr.net
www.borisfen-pro.ks.ua
Редакція авторів
Комп’ютерна правка та верстка авторів
Свідоцтво про внесення суб’єкта видавничої справи до Державного реєстру видавництв, виготовників і розповсюджувачів видавничої продукції ХС № 76 від 02.05.2012 року
_______________________________________________________Підписано до друку 22.01.2016р. Формат 60х84/16
Папір офсетний. Ум. друк. док. 23. Тираж 30 прим.






