Наименьшее значение центрально приложенной сжимающей силы, при которой прямолинейная форма равновесия стержня становится неустойчивой и потеря устойчивости протекает в упругой области, называется эйлеровой силой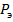 
. В такой постановке эта задача для шарнирно опертого призматического стержня по концам была впервые решена знаменитым математиком Леонардом Эйлером – членом Петербургской Академии наук – в 1744 году и поэтому часто называется задачей Эйлера.
Формулу для эйлеровой силы можно получить из дифференциального уравнения упругой линии стержня при продольном изгибе (рис. 10.3):
где M – изгибающий момент стержня в сечении х, равный 
(
– прогиб стержня).
Рисунок 10.3 – Продольный изгиб центрально сжатого /призматического стержня
Принимая функцию прогиба стержня в виде синусоиды и интегрируя уравнение (10.1) с определением постоянных интегрирования из граничных условий опирания стержня по концам, получаем формулу Эйлера:
где Е – модуль упругости материала; 
– минимальный момент инерции поперечного сечения стержня относительно главной центральной оси инерции; 
– длина стержня.
При потери устойчивости (выпучивании) стержня изгиб происходит, как правило, в плоскости, перпендикулярной к главной центральной оси инерции, относительно которой момент инерции минимален. Эта плоскость называется плоскостью наименьшей жесткости (рис. 10.4).
Рисунок 10.4 – Плоскость наименьшей жесткости в примере поперечного сечения стержня
Для прямоугольного поперечного сечения стержня (см. рис. 10.4) моменты инерции определяются по формулам:
Таким образом, при продольном изгибе стержня (см. рис. 10.3) в момент потери устойчивости поперечное сечение стержня поворачивается вокруг той оси, относительно которой момент инерции поперечного сечения стержня минимален.
Значение эйлеровой силы является численной характеристикой устойчивости стержня:
· при 
· при 
Формула Эйлера (10.2) обобщается на другие случаи граничных условий стержня введением понятия приведенной длины стержня:
где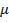 
– коэффициент приведенной длины, зависящий от граничных условий закрепления концов стержня (рис.10.5).
Рисунок 10.5 – Значения коэффициентов приведенной длины в зависимости от граничных условий стержня
Тогда формула Эйлера приобретет такой общий вид:
Нормальные напряжения, соответствующие эйлеровой силе, называются эйлеровыми напряжениями:
где 
– гибкость стержня
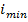– минимальный радиус инерции сечения стержня
Из анализа формул (10.5) и (10.6) можно указать пути повышения устойчивости стержня:
1) использование материалов с более высокими прочностными свойствами (Е);
2) увеличение сечения стержня ();
3) уменьшение длины стержня (l);
4) увеличение жесткости опорных закреплений стержня (например, при жесткой заделке концов стержня 
увеличивается в два раза по сравнению с шарнирным оперением).
