Общие положения о сложном сопротивлении
До сих пор рассматривались простейшие виды деформаций, при которых в поперечных сечениях брусьев (балок) возникал один вид внутренних факторов от растяжения (сжатия), сдвига, смятия, кручения, чистого изгиба. Исключение составляет прямой поперечный изгиб балок, когда в сечении х возникают два внутренних силовых фактора – перерезывающая сила и изгибающий момент. Однако и этот вид деформации относят к простейшим, так как, в основном, расчеты на прочность элементов конструкций ведут по изгибающему моменту, определяющему вычисление наибольших нормальных напряжений.
В то же время на практике ряд частей машин, механизмов, элементов конструкций подвергаются одновременно действию нескольких видов деформаций. Так, коленчатые валы машин и механизмов подвергаются действию изгиба и кручения, стойки подкрановых балок – сжатию и изгибу и др. Подобные случаи, сопровождающиеся комбинацией простейших деформаций, называют сложным сопротивлением. При этом в поперечных сечениях брусьев (балок) будет действовать более одного внутреннего силового фактора.
В расчетах на сложное сопротивление исходят из принципа независимости действия сил, когда результат совместного действия нескольких видов деформаций получают суммированием результатов каждого вида деформаций отдельно. Опыт показывает справедливость такого принципа в упругой области работы материала конструкций.
Рассмотрим несколько видов сложного сопротивления: косой изгиб; сочетание изгиба с растяжением (сжатием); совместное действие изгиба и кручения.
Косой изгиб
Косым изгибом называется такой вид изгиба, при котором плоскость действия изгибающего момента в данном поперечном сечении бруса не проходит ни через одну из главных центральных осей инерции этого сечения. Различают плоский косой изгиб (все внешние силы лежат в одной плоскости, а упругая линия – плоская кривая) и пространственный изгиб (внешние силы действуют в различных плоскостях, упругая линия – пространственная кривая).
Рассмотрим наиболее простой случай плоского косого изгиба, который в дальнейшем будем называть просто косым изгибом.
| Рисунок 9.1 – Косой изгиб бруса |
Пусть брус прямоугольного поперечного сечения, защемленный одним концом (рис.9.1), изгибается силой Р, действующей перпендикулярно к оси бруса на свободном конце и составляющей угол 
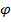к оси y. Разложим силу Р на составляющие ее проекции:
Тогда абсолютные значения изгибающих моментов от этих проекций силы Р в сечении х будут:
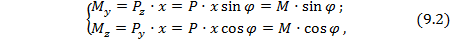
где 
– изгибающий момент, действующий вокруг оси y в плоскости 
; 
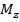– изгибающий момент, действующий вокруг оси z в плоскости 
; 
– результирующий изгибающий момент в сечении х, равный 
Моменты и 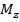действуют в главных плоскостях инерции сечения бруса. Напряжения и прогибы от каждого из этих моментов, взятых в отдельности, уже определялись ранее. Пользуясь принципом независимости действия сил, можно найти напряжения и прогибы, при одновременном действии моментов и 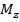. Таким образом, случай косого изгиба (рис. 9.2, а) можно всегда свести к двум плоским (поперечным), или, как говорят, к простым изгибам.
Рисунок 9.2 – Нагружения при косом изгибе
При действии только одного момента 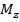нейтральной линией будет ось z (рис. 9.2, б) и нормальное напряжение для какой-либо точки N с координатами y и z, взятой в первом квадрате сечения mn (см. рис. 9.1), определяется по формуле:
Напряжение в той же точке от действия момента (рис. 9.2, в) равно:
При одновременном действии двух моментов и 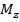напряжение в любой точке сечения будет равно алгебраической сумме напряжений 
и 
, т.е.
В эту формулу координаты y и z точек сечения и изгибающие моменты и 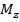подставляются со своими знаками. Если момент действует таким образом, что в 1-й четверти, где координаты y и z положительны, он вызовет растяжение, то ему приписывается знак «+», а если сжатие, – то «
».
Наибольшее суммарное напряжение в рассматриваемом случае будет в точках В и С: в т. В (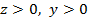
) – напряжение растяжения, а в точке С (
) – напряжение сжатия. Уравнение нейтральной линии (рис. 8.50, г) получим, приравнивая нулю правую часть формулы (9.5):
или
откуда
Этому уравнению прямой линии удовлетворяют значения 
следовательно, нейтральная линия проходит через центр тяжести поперечного сечения.
Определив из последнего выражения отношение 
, найдем тангенс угла 
, составляемого нейтральной линией и положительным направлением оси z (рис. 9.2, г):
Из формулы (9.7) видно, что для таких сечений, у которых 
(квадрат, круг), нейтральная линия будет перпендикулярна к плоскости действия изгибающего момента, в котором и будет происходить деформация изгиба.
В тех же случаях, когда 
и 
или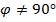 
, нейтральная линия не будет перпендикулярна к плоскости действия изгибающего момента.
Из рассмотренного примера следует, что наиболее напряжены будут точки В и С сечения бруса в месте его заделки, как наиболее удаленные при нейтральной линии. Тогда условие прочности для опасной точки В запишется в виде:
где 
, 
– координаты опасной точки В.
Прогибы при косом изгибе определяются как геометрическая сумма прогибов в координатных плоскостях:
где 
– прогибы балки в плоскостях соответственно yOx и zOx, которые вычисляются как и при прямом изгибе.
