Пример 9.1. Косой изгиб бруса. На брус прямоугольного поперечного сечения, защемленного левым концом (рис. 9.7), действуют вертикальная и горизонтальная силы Р, каждая величиной 
Длина 
соотношение размеров прямоугольного сечения бруса 
Найти размеры сечения, если допускаемое напряжение материала бруса 
Рисунок 9.7 – Косой изгиб бруса
Решение
Максимальное напряжение при изгибе бруса будет в т. А его сечения в месте защемления:
где 
– изгибающий момент бруса в плоскости 
,
– изгибающий момент бруса в плоскости 
,
;
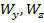– моменты сопротивления сечения бруса относительно координатных осей, 
Внося в формулу (9.18) выражения для изгибающих моментов и учитывая соотношение сторон сечения бруса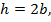 
получаем:
откуда
Тогда
Округляя размеры сечения бруса в большую сторону, получаем: 
Пример 9.2. Изгиб с растяжением балки. Для стальной балки коробчатого поперечного сечения, защемленной левым концом, подобрать размеры поперечного сечения (рис.9.8,а). Исходные данные: 
; 
| Рисунок 9.8 – Изгиб балки в двух плоскостях, испытывающей растяжение |
Решение
1. Условие прочности балки при изгибе с растяжением имеет вид:
где 
– усилие растяжения балки; 
– изгибающие моменты балки в плоскостях соответственно 
и ; 
моменты инерции сечения балки относительно осей координат.
2. Опасным сечением балки при изгибе будет место ее защемления в т. О, а опасными точками этого сечения будут точки С (при изгибе в вертикальной плоскости ) и D (при изгибе в горизонтальной плоскости ) – см. рис. 9.8, б.
3. Запишем выражение усилий 
по участкам балки с определением их значений для характерных сечений:
1) Участок СВ: 
; 
при 
; при 
. 
при 
2) Участок ОВ: 
; ; 
; 
при 
; 
; при 
4. Строим эпюры (рис. 9.10, б, г, д).
5. Анализируем эпюры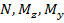 
и находим максимальные по абсолютной величине внутренние усилия в жесткой заделке балки: 
.
6. Определим необходимые геометрические характеристики поперечного сечения (см. рис. 9.10, б):
7. Подставив значения 
в условие прочности (9.18), получим:
Решив это уравнение относительно размера сечения балки a, найдем 
см.
Пример 9.3. На валу, приводимом в движение мотором М, насажен посредине шкив весом 
и диаметром 
(рис. 9.9). Натяжение ведущей части ремня, надетого на шкив, равны 
а ведомой – 
. Определить диаметр вала d, если допускаемое напряжение материала вала 
расстояние между опорами вала 
Рисунок 9.9 – Совместное действие на вал изгиба и кручения
Решение
Перенеся силы натяжения ремней в центр вала т. О, находим, что на вал действует горизонтальная сила величиной
и крутящий момент
Рисунок 9.10 – Эпюры изгибающего и крутящего моментов
Горизонтальная сила 
и вертикальная сила, представляющая собой вес шкива 
действуют в одном сечении вала. Их равнодействующая будет равна:
Максимальный изгибающий момент от этой равнодействующей будет находится посредине вала, и его величина составит:
Эпюры 
и 
представлены на рис.9.12, а, б.
По 3-й теории прочности наибольших касательных напряжений условие прочности вала имеет вид:
или выражая напряжения через изгибающий и крутящий моменты с учетом того, что 
откуда момент сопротивления сечения вала будет равен:
Так как для круглого сечения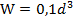 
, находим требуемый диаметр вала:
Принимаем 
