Пример 3.1. Рассчитать элементы растяжения-сжатия бруса (рис. 3.2) при следующих исходных данных: Р1=100 кН; Р2= 40 кН; Р3= 30 кН; F1= 20 см2; F2= 15 см2; F3= 10 см2; l1 = 0,5 м; l2 = 0,65 м; l3 = 0,55 м. Построить эпюры N, σ, 𝓌.
Решение
1. Определим реакцию закрепления бруса R из условия статики (см. рис. 3.2):
Реакция оказалась отрицательной, следовательно, на рисунке меняем ее направление (перечеркиваем прежнее направление и указываем обратное – см. рис. 3.2). При новом направлении реакции в последующих расчетах считаем ее положительной.
2. Используя метод сечений, определяем величину продольных сил в поперечных сечениях бруса по принятым участкам (рис. 3.3, а). Удобно начинать расчет с третьего участка, поскольку в выражения для N будут входить меньше усилий (рис. 3.3, б):
- участок III (рис. 3.2, б): 
; 
- участок II (рис. 3.2, в): ; 
- участок I (рис. 3.2, г): ; 
Рисунок 3.3 – Сечения бруса по участкам и эпюры N, σ, 𝓌
На основании выполненных расчетов строим эпюру продольных сил N (рис. 3.3, д).
3. Определим величину нормальных напряжений в поперечных сечениях бруса по участкам:
Строим эпюру нормальных напряжений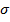 
(рис. 3.2, ж). Знак минус свидетельствует о напряжениях сжатия.
4. Определим величину абсолютных деформаций участков бруса:
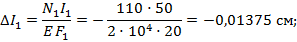
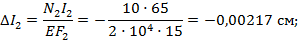
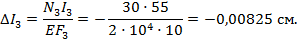
Знак «-» свидетельствует о деформации укорочения участков бруса
5. Определим абсолютную деформацию всего бруса:
Следовательно, брус при загружении испытывает деформацию укорочения.
6. Определим перемещения границ участков относительно верхней жесткой заделки:
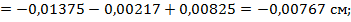
Строим эпюру перемещений границ участков бруса 𝓌 (рис. 3.2, з).
Пример 3.2. Рассчитать элементы растяжения-сжатия бруса (рис. 3.3) и построить их эпюры при следующих исходных данных: 
Решение
1. Определим реакцию закрепления бруса R из условия статики (см. рис. 3.4):
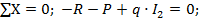
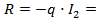
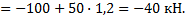
Реакция получилась отрицательной, ее первоначальное направление перечеркиваем и направляем R в обратную сторону (см. рис. 3.4.).
2. Используя метод сечений, определим величину продольных сил по участкам бруса (координату х отсчитываем от заделки бруса (рис. 3.5, а, б):
Рисунок 3.5 – Сечения бруса по участкам и эпюры N, σ, 𝓌
- участок I: 
; 
- участок II: 
, т.е. 
; 
при 
при 
Строим эпюру N по участкам бруса (рис. 3.5, г).
3. Определяем величину нормальных напряжений в поперечных сечениях по участкам бруса:
На основании выполненных расчетов строим эпюру σ (рис.3.5, д).
4. Определим абсолютные продольные деформации участков бруса:
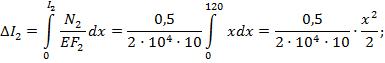
Обращаем внимание, что на втором участке по длине действия распределенной нагрузки интенсивностью q закон изменения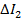 
будет нелинейным – по квадратичной параболе.
5. Определим абсолютное удлинение всего бруса:
6. Вычислим перемещения границ участков бруса относительно верхней жесткой заделки:
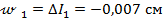(перемещение вверх);
(перемещение вниз).
Строим эпюру 
перемещений участков бруса (рис.3.5, ж).
