Деформации связаны с изменением формы и размеров тела при нагружении. В пределах малых деформаций различают линейные и угловые деформации.
Если выделить в окрестности точки А элементарный отрезок длиной 
, размеры которого малы по сравнению с размерами тела, то после нагружения тела длина отрезка измениться на величину 
(рис.2.4, а).
Линейной относительной деформацией в точке тела называется предел отношения абсолютного удлинения (укорочения) элементарного отрезка после нагружения к первоначальной длине отрезка до нагружения тела при «стягивании» отрезка в точку:
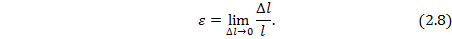
При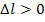 
– это удлинение, при 
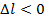– укорочение. Линейная относительная деформация 
безразмерна.
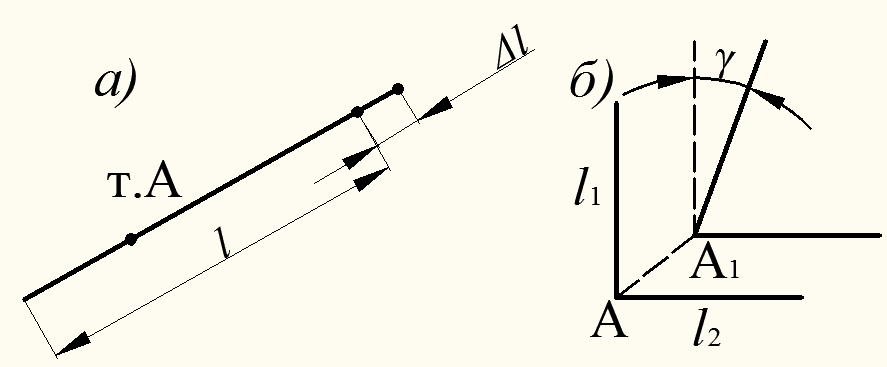
Рисунок 2.4 - Линейная и угловая деформация в точке тела
В случае действия на стержень продольной силы происходит его относительное удлинение (укорочение), которое можно назвать продольным и обозначить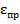 
. Однако наряду с этой деформацией происходит и относительная деформация стержня в поперечном направлении 
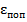. При этом для 
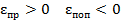, а для 
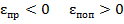. Тогда можно записать:
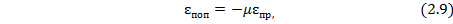
где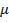 
– коэффициент, определяемый экспериментально и называемый коэффициентом Пуассона (для стали 
).
Величина зависит не только от положения точки в теле, но и от направления элементарного отрезка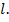 
Поэтому обычно к букве приписывают внизу индекс направления координатных осей, например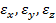 
.
При выделению у точки А двух взаимно перпендикулярных отрезков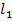 
и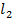 
они после деформации тела изменяют свой угол на величину 
(рис. 2.4, б). Тогда изменение первоначально прямого угла между отрезком в предположении малых деформаций называют угловой деформацией , которая выражается в радианах (рад). С учетом направлений отрезков к букве обычно приписывают индексы направления осей, например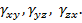 
Связь напряжений и деформаций упругого тела выражаются законом Гука:
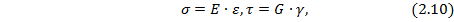
где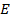 
– модуль упругости материала (модуль первого рода, или модуль Юнга), определяемый экспериментально (для стали 
); 
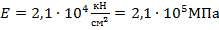– модуль сдвига (см. п. 4.1.).
В задачах сопротивления материалов изучают четыре простейших видов деформаций. К их числу относятся следующие:
1. Осевое растяжение и сжатие. При таком нагружении внутренние силы упругости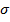 
могут быть заменены их равнодействующей – продольной силой 
(рис.2.5):
а) растяжение
| +N |
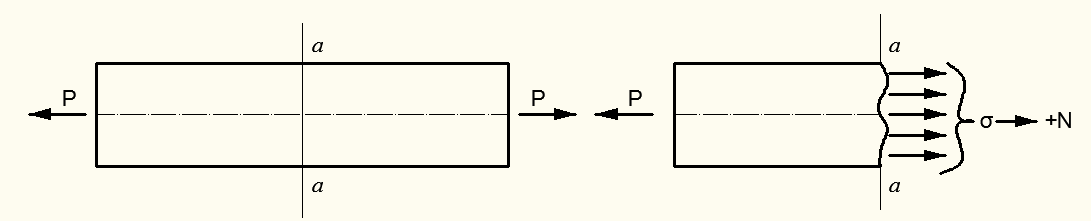
б) сжатие
| – N |
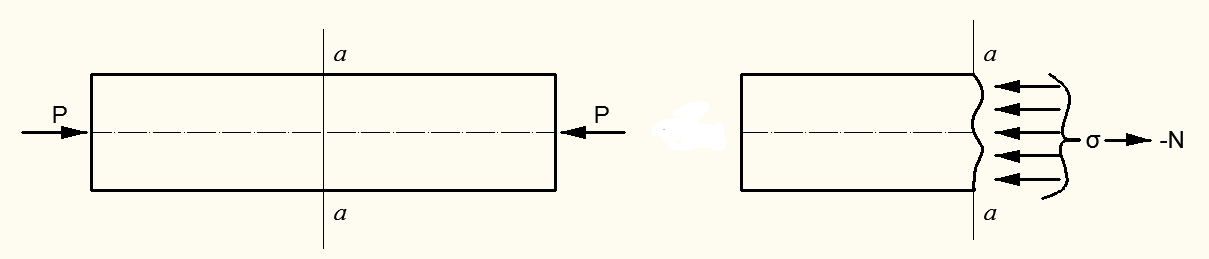
Рисунок 2.5 – Деформация растяжения (сжатия)
2. Сдвиг (срез). Эта деформация возникает тогда, когда касательные напряжения 
в плоскости сечения стержня приводят лишь к одной перерезывающей силе 
(рис. 2.6).
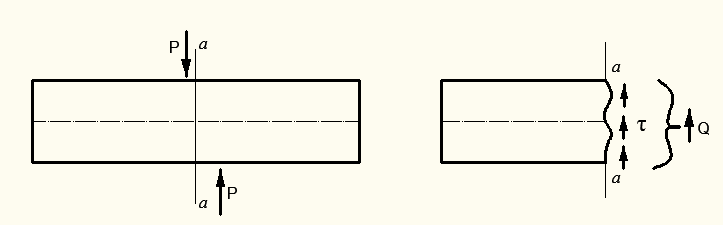
Рисунок 2.6 – Деформация сдвига (среза)
3. Кручение. При этом виде деформации от внешних закручивающих моментов стержня 
в его поперечных сечениях возникают касательные напряжения , приводящие к крутящему моменту 
(рис. 2.7). При кручении ось стержня остается прямой, а поперечные сечения поворачиваются вокруг оси стержня относительно друг друга на некоторый угол.
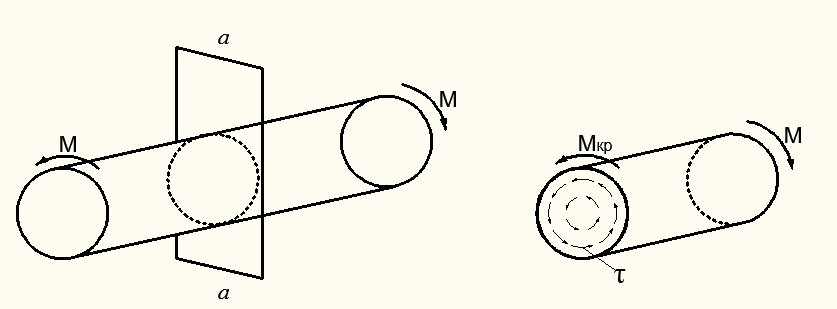
Рисунок 2.7 – Деформация кручения
4. Изгиб. Этот вид деформации возникает при действии внешней нагрузки поперек оси стержня (балки). Часто встречающимся случаем является поперечный изгиб балки, когда внешняя нагрузка приложена перпендикулярно оси балки в координатной плоскости 
(рис.2.8). В поперечном сечении балки а-а возникает две равнодействующие внутренних сил упругости: перерезывающая сила – равнодействующая касательных напряжений в плоскости сечения; изгибающий момент , к которому приводят нормальные напряжения 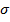, действующие перпендикулярно плоскости сечения балки.
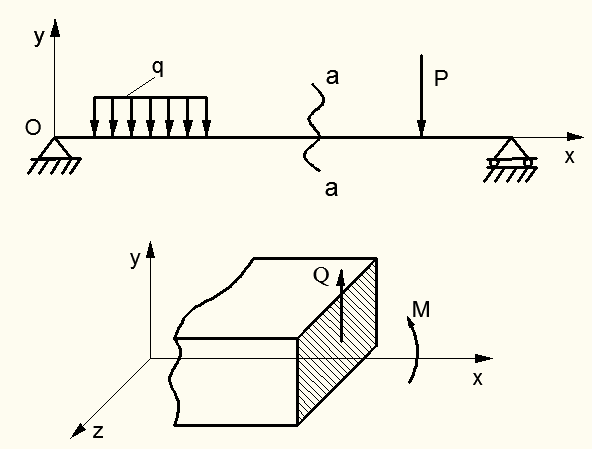
Рисунок 2.8
