Моменты инерции сечения и их виды

 

Различают следующие виды моментов инерции сечений: осевые; центробежный; полярный; центральные и главные моменты инерции.

(5.7)

Осевыми (экваториальными) моментами инерции сечения называют пределы сумм произведений элементарных площадок ΔF площади сечения F на квадраты расстояний их центров тяжести у и z до соответствующих осей (см.рис.5.3,б), что выражается интегралами вида

(5.8)

Центробежные моменты инерции сечения относительной у и z называют интеграл вида

(5.9)

Интеграл вида

называют полярным моментом инерции сечения относительно т. О.

(5.10)

Сумма осевых моментов инерции сечения относительно двух координатных осей равна полярному моменту инерции относительно начала координат:

Размерность указанных видов моментов инерции сечения (длина⁴), т.е. м⁴ или см⁴.

Осевые и полярный моменты инерции сечения – величины положительные; центробежный момент инерции может быть положительным, отрицательным и равным нулю (для некоторых осей, являющихся осью симметрии).

Существуют зависимости для моментов инерции при параллельном переносе и повороте координатных осей.

 

 

Рисунок 5.4 – Параллельный перенос и поворот координатных осей для произвольного поперечного сечения бруса

 

(5.11)

При параллельном переносе осей (рис. 5.4, а) момент инерции сечения относительно любой оси, проведенной параллельно центральной оси (проходящей через центр тяжести сечения т. С) равен моменту инерции относительно этой центральной оси плюс произведение площади сечения на квадрат расстояния между осями:

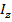где и 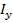– центральные моменты инерции.

(5.12)

Для центробежных моментов инерции

Если известны моменты инерции сечения Iz, Iу, Izу относительно осей z и у, то моменты инерции относительно повернутых осей z₁ и у₁, на угол α по отношению к исходным осям (рис. 5.4, б) определяется по формулам:

С понятием главных моментов инерции связывают положение главных осей инерции. Главными осями инерции называют две взаимно перпендикулярные оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты приобретают экстремальные значения (максимум и минимум).

Если главные оси проходят через центр тяжести фигуры, то они называются главными центральными осями инерции.

(5.14)

Главные моменты инерции вычисляются по формуле:

(5.15)

Положение главных осей инерции находят из следующих зависимостей:

В расчетах прочности элементов конструкций пользуются понятием такой геометрической характеристики как момент сопротивления сечения.

Рассмотрим для примера поперечное сечение бруса (рис. 5.5).

 

 

Рисунок 5.5 – Пример поперечного сечения бруса

 

 

Отстояние наиболее удаленной т. А от центра тяжести сечения т. С о бозначим h₁, а отстояние т. В – через h₂.

(5.16)

Тогда моменты сопротивления сечения относительно горизонтальной оси z точек А, В вычисляются как отношения осевого момента инерции относительно оси z к расстояниям до точек А, В:

Практический интерес в расчетах прочности представляет наименьший момент сопротивления сечения Wmin, соответствующий наиболее удаленной т. А от центра тяжести сечения h₁ = у_max.

Размерность элементов сопротивления (длина³), т.е. м³, см³.

Таблица 5.1 – Значения моментов инерции и моментов сопротивления простейших сечений относительно центральных осей

Виды наименования сечения	Моменты инерции	Моменты сопротивления
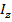
Прямоугольник
Круг

продолжение таблицы 5.1

Кольцо
Эллипс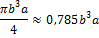