Графическое представление текстур

Анизотропные материалы

Электронные методические указания к лабораторным работам

САМАРА

2013

Составители: Михеев Владимир Александрович,

Журавель Леонид Васильевич

Анизотропные материалы [Электронный ресурс]: электрон.метод. указания к лаб. работам / Минобрнауки России, Самар. гос. аэрокосм. ун-т им. С. П. Королева (нац. исслед. ун-т); сост. В. А. Михеев, Л. В. Журавель. - Электрон.текстовые и граф. дан. (1,65 Мбайт). - Самара, 2013. - 1 эл. опт.диск (CD-ROM).

Методические указания предназначены для выполнения лабораторных работ в рамках курса «Анизотропные материалы» для подготовки магистров по направлению 150400.68 «Металлургия» факультета ИТФ.

©Самарский государственный

аэрокосмический университет, 2013

СОДЕРЖАНИЕ

ЛАБОРАТОРНАЯ РАБОТА 1. 4

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 4

1. Понятие текстуры.. 4

2. Графическое представление текстур. 5

3. Полюсные фигуры и рентгенограммы.. 8

4. Практика съемки рентгенограмм.. 9

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ. 11

5. Съемка рентгенограммы текстурованного образца в камере РКВ-86. 11

6. Порядок выполнения работы.. 12

Контрольные вопросы.. 13

Список рекомендуемой литературы.. 14

Приложение. 15

ЛАБОРАТОРНАЯ РАБОТА 2. 16

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 16

1. Основные положения рентгенографического метода определения текстур. 16

2. Обратные полюсные фигуры.. 17

3. Сущность определения текстуры методом ОПФ.. 18

4. Изготовление образца и эталона. 20

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ. 22

5. Проведение рентгеновской съемки. 22

6. Порядок расчета и построения обратных полюсных фигур. 22

7. Интерполяция обратных полюсных фигур. 23

8. Точность метода. 24

Список рекомендуемой литературы.. 25

Приложение. 26

ЛАБОРАТОРНАЯ РАБОТА 1

РЕНТГЕНОАНАЛИЗ ТЕКСТУР

Цель работы - ознакомиться с краткой теорией и одной из методик исследования текстур в металлах.

Приборы и принадлежности: рентгеновский аппарат УРС-55а, рентгеновская камера РКВ-86 с плоской кассетой, образцы алюминиевой проволоки.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Понятие текстуры

Текстурой называется преимущественное расположение зерен (кристаллитов) в поликристаллическом материале, кристаллографически ориентированное относительно внешней системы координат (см. таблицу)

Причина образования текстур - анизотропия внешних воздействий при обработке материала или получении изделия. Преимущественная ориентировка зерен становится причиной анизотропии свойств материала, чем и обусловлен практический интерес к явлению.

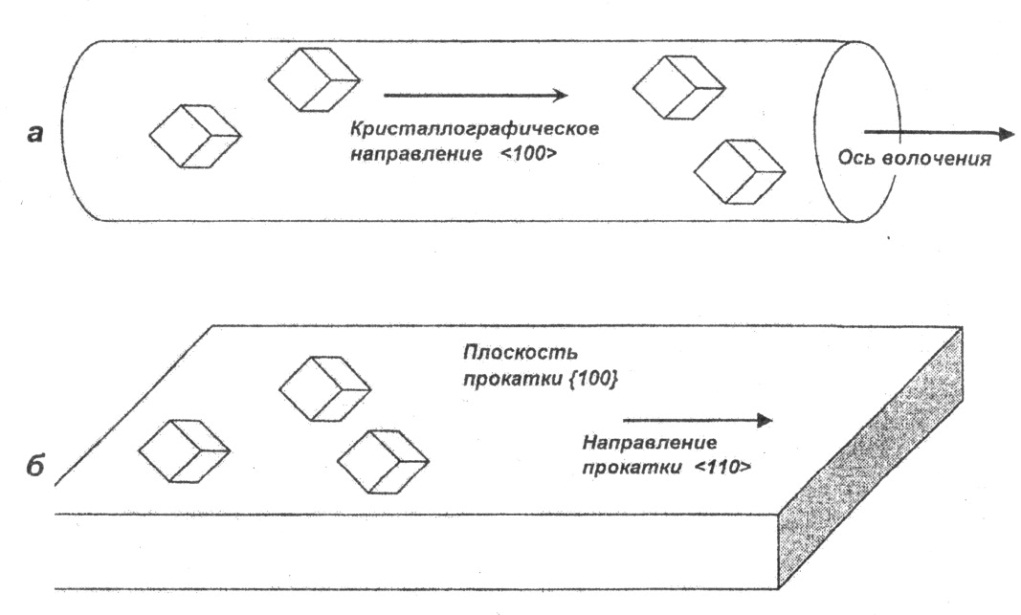
Рис. 1. Вид текстуры: а - аксиальная; б - прокатки

Текстура называется однокомпонентной, если преимущественная ориентировка одна, и многокомпонентной в случае нескольких ориентировок. В реальных условиях ориентировки отдельных кристаллитов не всеточно соответствуют «идеальной», а сосредоточены в пределах некоторого угла вокруг направления текстуры. Такой угол называется рассеянием текстуры.

Аксиальная (осесимметричная) текстура- вид текстуры, при котором все кристаллиты устанавливаются в определенном кристаллографическом направлении <uvw>, называемом осью текстуры (рис. 1, а). Такая текстура образуется в условиях сил, действующих в одном направлении (волочение, экструзия, сжатие, осаждение вдоль температурного или иного градиента, направленная кристаллизация).

Однокомпонентная осевая текстура обозначается индексами направления в угловых скобках (семейством эквивалентных направлений), многокомпонентная - суммой направлений: <u₁v₁w₁> + <u₂v₂w₂> +...

Ограниченной текстурой(текстурой прокатки) называется такая, при которой в кристаллитах образца фиксированными в определенном положении являются кристаллографическая плоскость {hkl} и направление <uvw>, лежащее в этой плоскости (рис. 2, б). Типичный пример ограниченной текстуры - текстура, возникающая при прокатке металлического сплава. В этом случае действуют силы сжатия по нормали к плоскости прокатки и растяжения вдоль направления прокатки. В результате такой деформации определенные плоскости {hkl} в зернах поликристалла оказываются параллельными плоскости прокатки, а определенные направления <uvw> - параллельными направлению прокатки. Обозначение текстуры прокатки:

{hkl}<uvw>

для однокомпонентной и, соответственно,

{h₁k₁l₁}<u₁v₁w₁> + {h₂k₂l₂}<u₂v₂w₂>+...

для многокомпонентной текстуры.

Таблица 1

Текстура волочения для проволоки некоторых кубических металлов

Металл	Тип решетки	Доля кристаллитов, ориентированных в направлениях
<100>	<110>	<111>
а - Fe	ОЦК	-		-
Мо	ОЦК	-		-
AI	ГЦК	-	-
Си	ГЦК		-
Аи	ГЦК		-
Ag	ГЦК		-

Графическое представление текстур

В качестве средств количественного описания и исследования текстур применяются прямые и обратные полюсные фигуры, которые строятся по данным рентгеноструктурного анализа.

Прямой полюсной фигурой (ППФ) называется гномостереографическая проекция (ГСП) определенной совокупности кристаллографических плоскостей для всех кристаллитов (зерен) данного поликристалла, то есть это стереографическая проекция (рис. 2, а) нормалей к плоскостям {hkl} одного семейства (следы нормалей на воображаемой сфере). Этим она отличается от стандартной ГСП монокристалла - последняя дает картину нормалей к плоскостям {h_ik_il_i} всех семейств одного, определенным образом ориентированного кристалла.

Обратной полюсной фигурой (ОПФ) называют распределение полюсных плотностей Р_hkl Для заданного направления (А) в образце. ОПФ строится на стандартном треугольнике стереографической проекции направлений для монокристалла данной сингонии (рис. 2, б). Полюсная плотность на ОПФ показывает долю кристаллитов, полюсы плоскостей которых совпадают с указанным направлением в образце. Такая доля может трактоваться как вероятность совпадения кристаллографического направления в зернах текстурованного материала с заданным направлением А.

Рис. 2. Примеры полюсных фигур: а -прямая; б - обратная

Под стандартным треугольником понимают треугольник, выделенный на стандартной проекции монокристалла. Его вершины соединяют три главных направления: для кубической решетки [001], [011] и [111]; для гексагональной и тетрагональной решеток [001], [100] и [110] и т. д.

Цифры около различных полюсов стандартного треугольника соответствуют экспериментально определенным значениям полюсной плотности Р_hkl, полученным, как правило, по данным рентгеновской дифрактометрии (в условиях различных ориентировок образца относительно пучка).

Любая ППФ имеет центр полюсной фигуры и сферу проекций произвольного радиуса. Полюсами плоскостей будут точки пересечения нормалей к плоскостям со сферой проекций. Совокупность всех полюсов и будет составлять полюсную фигуру.

Вместо картины распределения полюсов на поверхности сферы обычно пользуются картиной распределения стереографических проекций полюсов на экваториальном круге, которую также называют полюсной фигурой.

Пусть на поверхности сферы имеется точка Р, которую необходимо стереографически спроектировать на экваториальный круг (круг проекций).Для этого надо сначала выбрать точкузрения. Если проектируемая точка находится на северном (верхнем) полушарии, то за точку зрения принимают южный полюс сферы, и наоборот. Проектируемую точку соединяют с точкой зрения линией, которую называют лучом зрения.

Стереографической проекцией полюса или гномостереографической проекцией плоскости, таким образом, будет точка пересечения луча зрения с экваториальным кругом. Так, на рис. 3 точка Р₁ является стереографической проекцией точки Р. Проекции точек северного полушария отмечают кружочками, а проекции точек южного - крестиками.

Рис. 3. Графическое изображение кристаллов: а - сфера и круг проекций; б - отсчет широты и долготы

Положение каждого полюса на сфере и круге проекций определяется его широтой и долготой.

Широта измеряется дугой большого круга от северного полюса, для которого , кюжному, для которого .

Долгота измеряется по экватору от точки пересечения начальной плоскости с экватором по направлению движения часовой стрелки, если смотреть с северного полюса на южный.

Для удобства сферу проекций, подобно глобусу, можно покрыть системой меридианов (точки постоянной долготы ) и параллелей (геометрическое место точек с постоянной широтой ).

Для измерения координат точек на круге проекций пользуются специальными сетками Вульфа или Болдырева (рис. 4), являющимися стереографическими проекциями меридианов и параллелей на экваториальный круг.

Сетка Болдырева выполнена с точки зрения северного (или южного) полюса. Проекции меридианов представляют собой радиусы, а параллелей - концентрические окружности.

В сетке Вульфа точка зрения располагается на экваторе. Меридианы проектируются дугами больших окружностей (их плоскости проходят через центр сферы), а параллели - дугами малых кругов.

Рис. 4. Сетка Болдырева (а) и сетка Вульфа (б)

В отличие от глобуса, широта отсчитывается по диаметрам круга проекций от для центра круга к периферии, где для внешней окружности . Углы от 90° до 180°- от внешней окружности к центру. Долгота отсчитывается от правой крайней точки горизонтального диаметра, для которой по внешней окружности круга проекций в направлении движения часовой стрелки. Внизу будет , слева , наверху .

Рис. 5. Текстура холоднокатаной вольфрамовой проволоки

Очевидно, что полюсная фигура образца без текстуры будет представлять собой сферу проекций, равномерно покрытую полюсами. Возьмем для примера образец холоднотянутой проволоки вольфрама с ОЦК- решеткой. Осью текстуры является направление [110]. Во всех кристаллитах это направление параллельно направлению протяжки (рис. 5). Теперь поместим образец в центр сферы проекций так, чтобы ось текстуры была направлена вдоль оси Z. Построим полюсную фигуру для плоскостей 100. Шесть плоскостей входят в данное семейство: (100), (010), (001), (0 0), ( 00), (00 ), и им соответствуют шесть полюсов (рис. 6): Р₁, Р₂, Р₃, Р ₄, Р ₅ и Р₆. В каждом кристаллите в процессе волочения фиксируется только одна диагональ, что позволяет ему занять в пространстве любое положение, вытекающее из вращения кристаллита вокруг оси проволоки (рис. 6)

Рис. 6. Схема, поясняющая построение полюсной фигуры

Поэтому совокупность нормалей к плоскостям {hkl} всех кристаллитов образует два конуса и экваториальный круг, которые пересекают сферу проекций по трем окружностям. Эти окружности называются поясами возможных положений (ПВП).

Итак, на сфере проекций полюсы плоскостей {hkl} располагаются не с равномерной плотностью, а сосредоточены лишь в поясах различных отражений. Ширина шарового пояса определяется углом рассеяния текстуры . Чем больше угол , тем больше ширина ПВП. Вид полюсной фигуры зависит от ориентировки образца в центре сферы проекций, т. е. от того, вдоль какой из осей координат расположена ось текстуры. Расположение оси текстуры вдоль оси у иллюстрирует рис. 7.

Рис. 7. Сферическая и стереографическая проекции

Полюсную фигуру можно построить и расчетным путем. Угол между осью текстуры и нормалью к плоскости в отражающем положении можно определить из выражения (1).

(1)

Для рассмотренного выше случая трем поясам возможных положений соответствуют углы