и, следовательно,  .
.
Ответ:  .
.
38. Измерение дисперсии показателя преломления оптического стекла дало  для
для  и
и  для
для 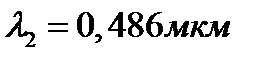 . Найти отношение фазовой скорости к групповой для света с длиной волны 0,434 мкм.
. Найти отношение фазовой скорости к групповой для света с длиной волны 0,434 мкм.
Дано:  ;
;  ;
; 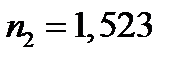 ;
;  .
.
Найти:  .
.
Решение. Фазовая скорость света равна
 , (1)
, (1)
а групповая скорость определяется как
 , (2)
, (2)
где n-показатель преломления;  -длина световой волны. Разделив выражение (1) на (2), найдем
-длина световой волны. Разделив выражение (1) на (2), найдем
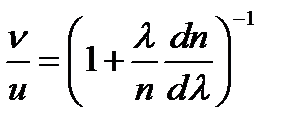 (3)
(3)
Для средней дисперсии показателя преломления в интервале длин волн от  до
до 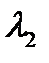 имеем
имеем
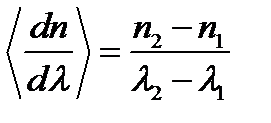
Проводя вычисления, получим
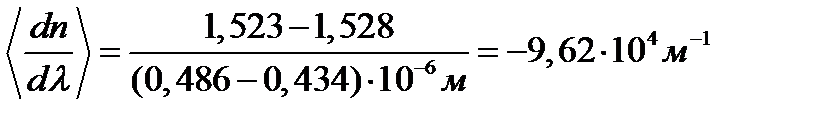 .
.
Подставляя в (3) значения  ,
,  и
и  , найдем
, найдем
 .
.
Ответ: 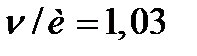 .
.
39. Определить импульс электронов, которые в среде с показателем преломления 1,5 излучают свет под углом 300 к направлению своего движения.
Дано:  ;
;  .
.
Найти: р.
Решение. Излучение Вавилова – Черенкова возникает, когда скорость движения  заряженной частицы в среде больше фазовой скорости в этой среде, равной
заряженной частицы в среде больше фазовой скорости в этой среде, равной  . Излучение направлено вдоль образующих конуса, ось которого совпадает с направлением движения частицы. Угол между направлением движения частицы определяется формулой
. Излучение направлено вдоль образующих конуса, ось которого совпадает с направлением движения частицы. Угол между направлением движения частицы определяется формулой
 . (1)
. (1)
Отсюда скорость частицы
 (2)
(2)
Импульс релятивистской частицы определяется как
 , (3)
, (3)
где  - масса покоя частицы. Подставляя (2) в (3), получим
- масса покоя частицы. Подставляя (2) в (3), получим
 . (4)
. (4)
Для электронов  . Подставляя в (4) числовые значения, найдем
. Подставляя в (4) числовые значения, найдем
 .
.
Ответ:  .
.
40. Энергетическая светимость черного тела равна 250 кВт/м2. определить длину волны, отвечающую максимуму испускательной способности этого тела.
Дано:  .
.
Найти:  .
.
Решение. Энергетическая светимость черного тела, согласно Стефана –Больцмана, равна
 , (1)
, (1)
где  -постоянная Стефана –Больцмана; Т- абсолютная температура тела.
-постоянная Стефана –Больцмана; Т- абсолютная температура тела.
Из (1) найдем
 . (2)
. (2)
Длина волны, на которую приходится максимум испускательной способности черного тела, согласно закону смещения Вина, определяется как
 , (3)
, (3)
где b- постоянная Вина.
Подставляя (2) в (3), получим
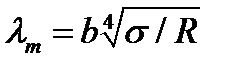 (4)
(4)
Проводя вычисления, найдем
 .
.
Ответ:  .
.
41. Определить давление света с длиной волны 550 нм, нормально падающего на зеркальную поверхность, если на 1см2 этой поверхности ежесекундно падает 1018 фотонов.
Дано: 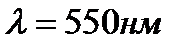 ;
; 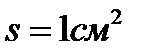 ;
;  ;
;  ;
;  .
.
Найти: р.
Решение. Давление света при нормальном падении на поверхность с коэффициентом отражения  определяется по формуле
определяется по формуле
 , (1)
, (1)
Где I – интенсивность света, равная энергии всех фотонов, падающих в единицу времени на единицу площади поверхности
 , (2)
, (2)
а энергия фотона и длина волны света связаны соотношением
 . (3)
. (3)
С учетом выражений (2) и (3) формулу (1) можно представить в виде
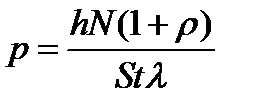 . (4)
. (4)
Подставляя в (4) числовые значения, получим
 .
.
Ответ: 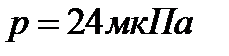 .
.
42. Красная граница фотоэффекта для никеля равна 0,257 мкм. Найти длину волны света, падающего на никелевый электрод, если фототок прекращается при задерживающей разности потенциалов, равной 1,5В.
Дано:  ;
;  .
.
Найти:  .
.
Решение. Согласно уравнению Эйнштейна,для фотоэффекта
 , (1)
, (1)
Где А- работа выхода электронов из металла;  - максимальная кинетическая энергия фотоэлектронов.
- максимальная кинетическая энергия фотоэлектронов.
Красная граница фотоэффекта определяется из условия равенства энергии фотона  работе выхода электронов, т.е.
работе выхода электронов, т.е.
 . (2)
. (2)
Максимальная кинетическая энергия фотоэлектронов может быть определена через задерживающую разность потенциалов
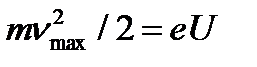 (3)
(3)
Подставляя (2) и (3) в (1), получим
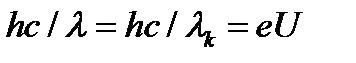 (4)
(4)
Из уравнения (4) найдем длину волны света
 (5)
(5)
Проведя вычисления, получим
 .
.
Ответ:  .
.
43. Гамма –фотон с длиной волны 1,2пм в результате комптоновского рассеяния на свободном электроне отклонился от первоначального направления на угол 600. Определить кинетическую энергию и импульс электрона отдачи. До столкновения электрон покоился.
Дано:  ;
;  .
.
Найти: Т; р.
Решение. Изменение длины волны фотона при комтоновском рассеянии на неподвижном свободном электроне равно
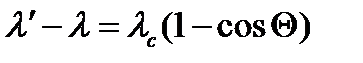 , (1)
, (1)
Где  - длина волны рассеянного фотона;
- длина волны рассеянного фотона; 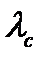 - комптоновская длина волны электрона,
- комптоновская длина волны электрона,  м.
м.
Из уравнения (1) найдем
 (2)
(2)
Выразим энергию падающего и рассеянного фотона через длину его волны:
 ;
; 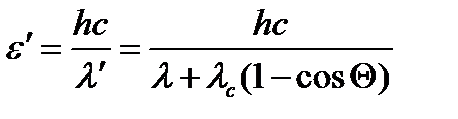 (3)
(3)
Кинетическая энергия электрона отдачи, согласно закону сохранения энергии, равна
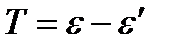 (4)
(4)
Подставляя выражения (3) в (4), получим
 (5)
(5)
Проводя вычисления, найдем

Зная кинетическую энергию электрона, найдем его импульс. Поскольку кинетическая энергия электрона сравнима с его энергией покоя 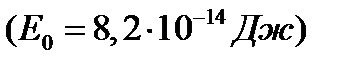 , импульс и кинетическая энергия связаны релятивистским соотношением
, импульс и кинетическая энергия связаны релятивистским соотношением
 (6)
(6)
Подставляя в (6) числовые значения, получим

Ответ:  ;
; 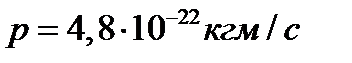 .
.
44. Кинетическая энергия протона в четыре раза меньше его энергии покоя. Вычислить дебройлевскую длину волны протона.
Дано:  ;
; 
Найти:  .
.
Решение. Длина волны де Бройля  определяется по формуле
определяется по формуле

 , (1)
, (1)
где h-постоянная Планка; р- импульс частицы.
Так как по условию задачи
 , (2)
, (2)
кинетическая энергия Т протона сравнима с его энергией покоя Е0, импульс р и кинетическая энергия связаны релятивистским соотношением
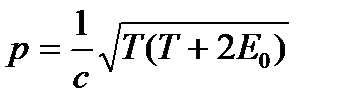 (3)
(3)
где с-скорость света в вакууме. Подставляя в (3) условие (2), найдем
 (4)
(4)
Учитывая равенство (4), запишем (1) в виде
 (5)
(5)
Подставляя в (5) числовые значения, получим
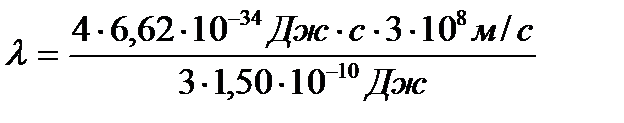
Ответ: 
45. Масса движущегося электрона в три раза больше его массы покоя. Чему равна минимальная неопределенность координаты электрона?
Дано: m=3m0;m0=0,91·10-30 кг.
Найти:  .
.
Решение. Согласно соотношению неопределенности Гейзенберга,
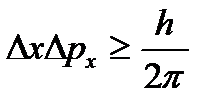 (1)
(1)
где 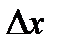 и
и  - неопределенности координаты и импульса частицы;
- неопределенности координаты и импульса частицы;
h-постоянная Планка.
Учитывая, что

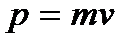 (2)
(2)
где m-масса; v- скорость частицы, соотношение (1) можно представить в виде
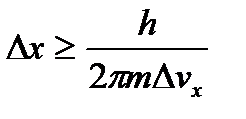 (3)
(3)
Поскольку неопределенность скорости 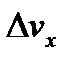 , как и сама скорость, не может превышать скорость света с в вакууме, то
, как и сама скорость, не может превышать скорость света с в вакууме, то
 . (4)
. (4)
Согласно условию,
 . (5)
. (5)
Подставляя в (4) условие (5), получим
 (6)
(6)
Проведя вычисления, найдем
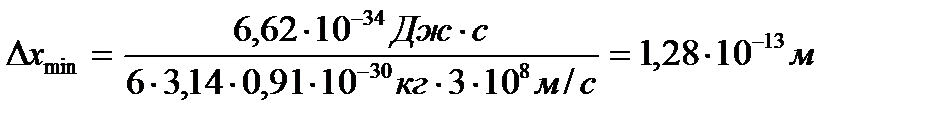 .
.
Ответ:  .
.
46. Частица находится в бесконечно глубокой одномерной потенциальной яме шириной l на втором энергетическом уровне. В каких точках ямы плотность вероятности обнаружения частицы совпадает с классической плотностью вероятности.
Дано: l; 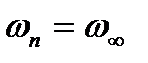 ; n=2.
; n=2.
Найти: x.
Решение. Волновая функция  , описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме шириной l, имеет вид
, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме шириной l, имеет вид
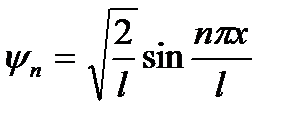 (1)
(1)
где n-номер энергетического уровня (т=1, 2,3, …); х- координата частицы в яме  .
.
Согласно физическому смыслу волновой функции,
 , (2)
, (2)
где  - плотность вероятности обнаружения частицы в точке с координатой х.
- плотность вероятности обнаружения частицы в точке с координатой х.
Если частица находится на втором энергетическом уровне (n=2), то
 . (3)
. (3)
В соответствии с принципом соответствия Бора, выражение для классической плотности вероятности получается при 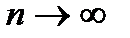
 . (4)
. (4)
Приравнивая по условию задачи выражение (3) к (4), получим
 . (5)
. (5)
Решая уравнение (5), найдем
 k=0,
k=0,  (6)
(6)
В пределах ямы  таких точек четыре:
таких точек четыре:
 .
.
Ответ:  .
.
47. Вычислить дефект массы, энергию связи и удельную энергию связи ядра 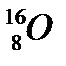 .
.
Решение. Дефект массы 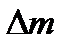 ядра определяется по формуле
ядра определяется по формуле
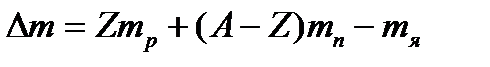 , (1)
, (1)
где Z-зарядовое число; А- массовое число; mp- масса протона;  -масса нейтрона;
-масса нейтрона;  - масса ядра.
- масса ядра.
Формулу (1) можно также записать в виде
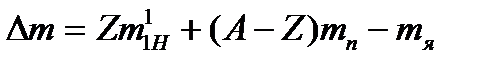

где  -масса атома
-масса атома  ;
;  - масса атома, дефект массы ядра которого определяется.
- масса атома, дефект массы ядра которого определяется.
Из справочных таблиц находим:
 а.е.м.;
а.е.м.;  а.е.м.;
а.е.м.;  а.е.м.
а.е.м.
Подставляя в (2) числовые данные (для  числа Z=8 и A=16), получим
числа Z=8 и A=16), получим
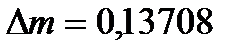 а.е.м.
а.е.м.
Энергия связи ядра  определяется по формуле
определяется по формуле
 , (3)
, (3)
где с- скорость света в вакууме.
Если дефект массы  выражать в
выражать в  , а энергия связи
, а энергия связи  - в
- в  , то формула (3) принимает вид
, то формула (3) принимает вид
 . (4)
. (4)
Подставляя в (4) числовые значения, получим
 .
.
Удельная энергия связи  вычисляется по формуле
вычисляется по формуле
 . (5)
. (5)
Проводя вычисления, получим
 .
.
Ответ: 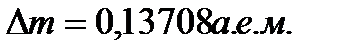 ;
; 

Контрольная работа №2
Таблица вариантов
| 1. | 11. | 21. | 31. | 41. | 51. | 61. | 71. | 81. | 91. | 101. | 111. | 121. | 131. | 141. | 151. | |
| 2. | 12. | 22. | 32. | 42. | 52. | 62. | 72. | 82. | 92. | 102. | 112. | 122. | 132. | 142. | 152. | |
| 3. | 13. | 23. | 33. | 43. | 53. | 63. | 73. | 83. | 93. | 103. | 113. | 123. | 133. | 143. | 153. | |
| 4. | 14. | 24. | 34. | 44. | 54. | 64. | 74. | 84. | 94. | 104. | 114. | 124. | 134. | 144. | 154. | |
| 5. | 15. | 25. | 35. | 45. | 55. | 65. | 75. | 85. | 95. | 105. | 115. | 125. | 135. | 145. | 155. | |
| 6. | 16. | 26. | 36. | 46. | 56. | 66. | 76. | 86. | 96. | 106. | 116. | 126. | 136. | 146. | 156. | |
| 7. | 17. | 27. | 37. | 47. | 57. | 67. | 77. | 87. | 97. | 107. | 117. | 127. | 137. | 147. | 157. | |
| 8. | 18. | 28. | 38. | 48. | 58. | 68. | 78. | 88. | 98. | 108. | 118. | 128. | 138. | 148. | 158. | |
| 9. | 19. | 29. | 39. | 49. | 59. | 69. | 79. | 89. | 99. | 109. | 119. | 129. | 139. | 149. | 159. | |
| 10. | 20. | 30. | 40. | 50. | 60. | 70. | 80. | 90. | 100. | 110. | 120. | 130. | 140. | 150. | 160. |
1. Тело, брошенное вертикально вниз с начальной скоростью 5 м/с, в последние 2 с падения прошло путь вдвое больший, чем в две предыдущие 2 с. Определить время падения и высоту, с которой тело было брошено. Построить графики зависимости пройденного пути, ускорения и скорости от времени.
2. Вверх по идеально гладкой наклонной плоскости, образующей угол 30° с горизонтом, пустили шайбу с начальной скоростью 12 м/с. Когда шайба достигла половины максимальной высоты подъема, из той же точки, в том же направлении и с той же скоростью пустили вторую шайбу. Определить: на каком расстоянии от начала наклонной плоскости встретятся обе шайбы; максимальную высоту подъема шайбы; промежуток времени, прошедший от начала движения первой шайбы до ее встречи со второй. Начертить графики зависимости пройденного пути, скорости и ускорения от времени для первой шайбы в промежуток времени от начала движения до момента встречи со второй.
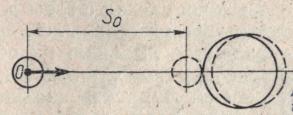
3. Шар, свободно движущийся со скоростью 6 м/с, ударился о другой шар и, двигаясь в обратном направлении со скоростью 2 м/с, вернулся в исходную точку (рис. 1.). Расстояние между исходным положением шара и его положением в момент соударения с другим шаром равно S0. Построить для промежутка времени от начала движения шара до момента его возвращения в исходное положение графики зависимости от времени скорости, модуля скорости, координаты центра шара на осиО х и проходимого им пути. Определить также среднее значение модуля скорости движения шара. Временем соударения шаров пренебречь.
|
Рис.1
4. Наблюдатель, стоящий на платформе, определил, что первый вагон электропоезда прошел мимо него в течение 4 с, а второй - в течение 5 с. После этого передний край поезда остановился на расстоянии 75 м от наблюдателя. Считая движение поезда равнозамедленным, определить его начальную скорость, ускорение и время замедленного движения. Начертить графики зависимости пути, скорости и ускорения поезда от времени. За начало отсчета времени принять момент прохождения мимо, наблюдателя переднего края поезда.
5. Наблюдатель, стоящий в момент начала движения электропоезда у его переднего края, заметил, что первый вагон прошел мимо него за 4 с. Определить время, за которое мимо него пройдут девять вагонов, а также время прохождения 9-го вагона. Во сколько раз скорость девятого вагона больше скорости пятого в моменты их прохождения мимо наблюдателя? Движение считать равноускоренным.
6. Тело, двигаясь прямолинейно с постоянным ускорением, прошло последовательно два равных участка пути, по 20 м каждый. Первый участок пройден за 1,06 с, а второй — за 2,2 с. Определить ускорение тела, скорость в начале первого и в конце второго участков пути, путь, пройденный телом от начала движения до остановки. Начертить графики зависимости пройденного пути, скорости и ускорения от времени.
7. С горы АВ (рис. 2) длиной 20 м из состояния покоя скатываются санки и затем, продолжая движение от точки В по горизонтальной плоскости, останавливаются у точки С, пройдя расстояние ВС, равное 15 м. Определить скорость санок в конце спуска с горы, ускорения на участках АВ и ВС и время спуска с горы. Весь путь ЛВС санки проходят за 15 с. Ускорение на каждом из участков (АВ и ВС) считать постоянным. Начертить графики зависимости пройденного пути, скорости и ускорения от времени.
8. Автомобиль трогается с места и первый километр проходит с ускорением а1 а второй – с ускорением а2. При этом на первом километре его скорость возрастает на 10 м/с, а на втором – на 5 м/с. Определить: время прохождения первого и второго километров; какое ускорение больше – а1 или а2 среднюю скорость на всем пути. Начертить графики зависимости пути, скорости и ускорения от времени.






