; (2)
- средняя длина свободного пробега молекул. Для нахождения воспользуемся формулой из примера 11:
. (3)
Подставляя (2) и (3) в выражение (1), имеем
(4)
Коэффициент внутреннего трения
,
где ρ- плотность газа при температуре 300 К и давлении 105 Па.
Для нахождения ρ воспользуемся уравнением состояния идеального газа. Запишем его для двух состояний азота – при нормальных условиях 
, 
и при заданных условиях:
; 
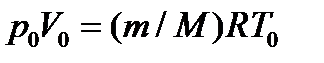(6)
Учитывая, что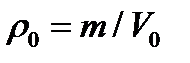 
, 
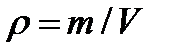, имеем
(7)
Коэффициент внутреннего трения газа может быть выражен через коэффициент диффузии (см. формулы (1) и (5)):
(8)
Подставляя числовые значения в (4) и (8), получим
;
.
Ответ: 
, 
.
14. Кислород массой 160 г нагревают при постоянном давлении от 320 до 340 К. Определить количество теплоты, поглощенное газом, изменение внутренней энергии и работу расширения газа.
Дано: 
, 
, 
.
Найти: Q; 
; А.
Решение. Количество теплоты, необходимое для нагревания газа при постоянном давлении
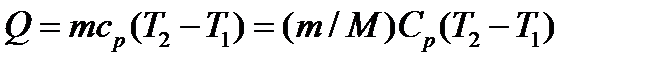. (1)
Здесь ср и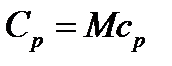 
-удельная и молярная теплоемкости газа при постоянном давлении; 
-молярная масса кислорода. Для всех двухатомных газов
; 
.
Изменение внутренней энергии газа находим по формуле
, (2)
Здесь ср и Ср=Мср–удельная и молярная теплоемкости газа при постоянном давлении; 
- молярная масса кислорода. Для всех двухатомных газов
; 
.
Изменение внутренней энергии газа находим по формуле
,
Где СV –молярная теплоемкость газа при постоянном объеме. Для всех двухатомных газов
; 
.
Работа расширения газа при изобарном процессе 
, где 
- изменение объема газа, которое можно найти из уравнения Клайперона –Менделеева. При изобарном процессе
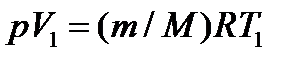; (3)
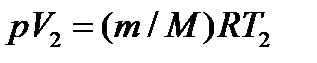(4)
Почленным вычитанием выражения (3) и (4) находим
,
Следовательно,
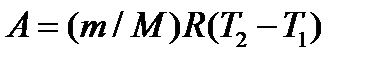. (5)
Подставляя числовые значения в формулы (1), (2) и (5), получаем:
;
;
.
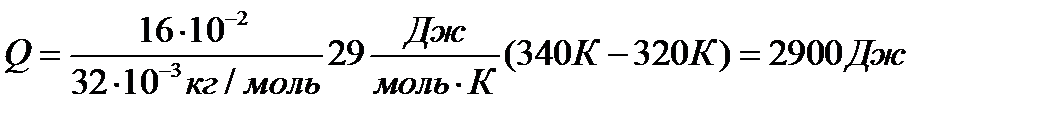Ответ: 
.
15. Объем аргона, находящегося при давлении 80 кПа, увеличился от 1 до 2 л. Насколько изменится внутренняя энергия газа, если расширение происходило: а) изобарно; б) адиабатно.
Дано: 
; 
; 
.
Найти: 
.
Решение. Применимпервый закон термодинамики. Согласно этому закону, количество теплотыQ, переданное системе, расходуется на увеличение внутренней энергии 
и на внешнюю механическую работу А:
. (1)
Величину 
можно определить, зная массу газа m, удельную теплоемкость при постоянном объеме 
и изменение температуры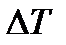 
:
(2)
Однако удобное изменение внутренней энергии определять через молярную теплоемкость СV, которая может быть выражена через число степеней свободы:
. (3)
Подставляя величину сv из формулы (3) в (2), получаем
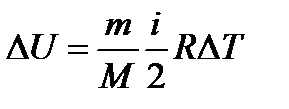(4)
Изменение внутренней энергии зависит от характера процесса, при котором идет расширение газа. При изобарном расширении газа, согласно первому закону термодинамики, часть количества теплоты идет на изменение внутренней энергии , которая выражается формулой (4). Найти для аргона по формуле (4) нельзя, так как масса газа и температура в условии задачи не даны. Поэтому необходимо провести преобразование формулы (4).
Запишем уравнение Клайперона –Менделеева для начального и конечного состояний газа:
; 
,
или
(5)
Подставив (5) в формулу (4), получим
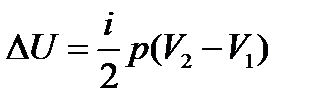(6)
Это уравнение является расчетным для определения при изобарном расширении.
При адиабатном расширении газа теплообмена с внешней средой не происходит, поэтому 
. Уравнение (1) запишется в виде
(7)
Это соотношение устанавливает, что работа расширения газа может быть осуществлена только за счет уменьшения внутренней энергии газа (знак минус перед ):
(8)
Формула работы для адиабатного процесса имеет вид
, (9)
где γ – показатель степени адиабаты, равный отношению теплоемкостей: 
. Для аргона – одноатомного газа 
- имеем 
.
Находим изменение внутренней энергии при адиабатном процессе для аргона, учитывая формулы (8) и (9):
(10)
Для определения работы расширения аргона формулу (10) следует преобразовать, учитывая при этом параметры, данные в условии задачи. Применив уравнение Клайперона –Менделеева для данного случая: 
, получим выражение для подсчета изменения внутренней энергии:
(11)
Подставляя числовые значения в (6) и (11), имеем:
а) при изобарном расширении
;
б) при адиабатном расширении
.
Ответ: а) 
б) 
.
16. Температура нагревателя тепловой машины 500 К. Температура холодильника 400 К. Определить КПД тепловой машины, работающей по циклу Карно, и полную мощность машины, если нагреватель ежесекундно передает ей 1675 Дж теплоты.
Дано: 
; 
.
Найти: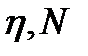 
.
Решение. Коэффициент полезного действия машины определяется по формуле
(1)
или
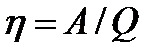. (2)
Из выражений (2) и (10 находим
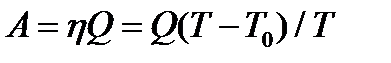
Вычислим:
;
.
Эта работа совершается за 1 с, следовательно, полная мащность машины 335 Вт.
Ответ: 
; 
.
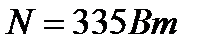17. Горячая вода некоторой массы отдает теплоту холодной воде такой же массы и значения их температуры становятся одинаковыми. Показать, что энтропия при этом увеличивается.
Решение. Пусть температура горячей воды Т1, холодной Т2, а температура смеси Θ. Определим температуру смеси, исходя из уравнения теплового баланса
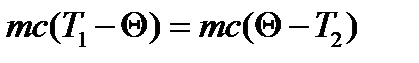, или 
,
откуда
(1)
Изменение энтропии, происходящее при охлаждении горячей воды,
Изменение энтропии, происходящее при нагревании холодной воды,
Изменение энтропии системы равно
,
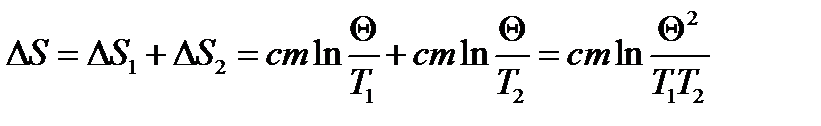или с учетом соотношения (1) имеем
.
Так как 
и 
, то 
.
18. Два одинаковых заряда находятся в воздухе на расстоянии 0,1 м друг от друга. Напряженность поля в точке, удаленной на расстояния 0,06 и 0,08 м от одного и другого зарядов, равна 10 кВ/м. Определить потенциал поля в этой точке и величину зарядов.
Дано: 
; 
; 
; 
; 
.
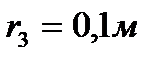Найти: 
; φ.
Решение. Напряженность Е и потенциал φ поля точечного заряда q определяется по формулам:
; 
,
Где ε – диэлектрическая проницаемость среды; ε0 – электрическая постоянная; r–расстояние от заряда до точки поля. Как видно из рис. 1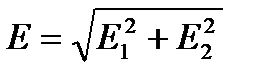 
, так как 
.
|
Рис. 1
Откуда:
.
Определим потенциал:
Ответ: 
19. Две параллельные плоскости одноименно заряжены с поверхностной плотностью зарядов 2 и 4 нКл/м2. Определить напряженность поля: а) между плоскостями; б) вне плоскостей.
Дано: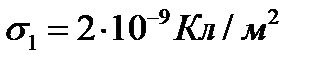 
; 
Найти: 
и 
.
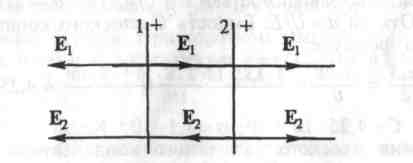
Решение. Как видно из рис. 2, в зазоре между плоскостями 
, так как направления векторов Е1 и Е2 противоположны. Тогда 
, где ε0 – электрическая постоянная.
|
.
Рис. 2
В пространствевне зазорамежду плоскостями векторы Е1 и Е2 совпадают по направлению. Поэтому
Ответ: 
20. Заряд величиной 1 нКл переносится из бесконечности в точку, находящуюся на расстоянии 0,1 м от поверхности металлической сферы радиусом 0,1 м, заряженной с поверхностной плотностью 10-5 Кл/м2. Определить работу перемещения заряда.
Дано: 
; 
; 
; 
.
Найти: А.
Решение. Потенциал поля 
, создаваемого заряженной сферой на расстоянии 
от ее центра, определяется по формуле:
,
где 
- заряд сферы;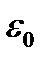 
- электрическая постоянная.
Потенциал поля на расстоянии 
равен нулю: 
. Работа А по перемещению заряда q из бесконечности в точку поля равна:
.
Ответ: 
.
21. Конденсатор с парафиновым диэлектриком заряжен до разности потенциалов 150В. Напряженность в нем равна 
, площадь пластин 6 см2. Определить емкость конденсатора и поверхностную плотность заряда на обкладках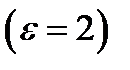 
.
Дано: 
; 
.
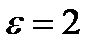Найти: С и σ.
Решение. В плоском конденсаторе напряженность поля 
, где ε – диэлектрическая проницаемость среды, ε0 – электрическая постоянная. Откуда
.
В плоском конденсаторе разность потенциалов U и напряженностьЕ связаны зависимостью 
, 
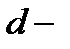зазор между обкладками. Откуда 
. Емкость С плоского конденсатора определяется по формуле:
.
Ответ: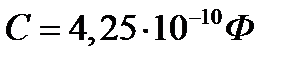 
; 
.
22. Энергия плоского воздушного конденсатора 40 нДж,разность потенциалов на обкладках 600 В, площадь платин 1см2.
Определить расстояние между обкладками, напряженность и объемную плотность энергии поля конденсатора.
Дано: 
; 
; 
; 
.
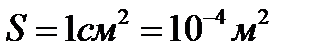Найти: в, Е, w.
Решение. Энергия конденсатора 
; емкость конденсатора 
, следовательно, 
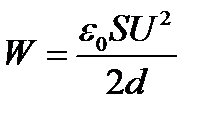. Отсюда
.
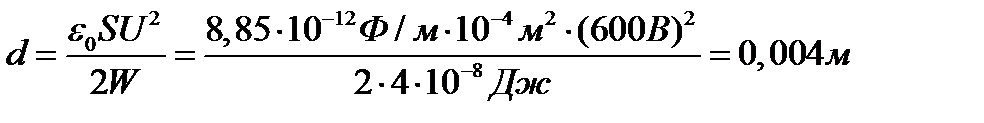Напряженность поля конденсатора
.
Объемная плотность энергии поля:
.
Ответ: 
; 
23. Плотность тока в никелиновом проводнике длиной 25 м равна 1 МА/м2. Определить напряжение на концах проводника.
Дано: 
.
Найти: U.
Решение. По закону Ома в дифференциальной форме плотность тока j в проводнике пропорциональна напряженности Е поля в проводнике 
, где 
-удельная проводимость; 
-удельное сопротивление проводника. С другой стороны 
, где U- напряженность на концах проводника длиной ℓ. Тогда 
, откуда 
.
Ответ: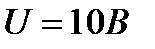 
.
24. Определить электродвижущую силу аккумуляторной батареи, ток короткого замыкания которой равен 10 А, если при подключении к ней резистора сопротивлением 2 Ом сила тока в цепи равна 1 А.
Дано: 
Найти: ε.
Решение. По закону Ома 
и 
где r-внутреннее сопротивление батареи. При коротком замыкании цепи внешнее сопротивление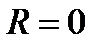 
и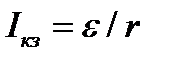 
, откуда 
. Тогда 
или 
.
Ответ: 
.
25. Изолированный прямолинейный проводник изогнут в виде прямого угла со стороной длиной 20 см. В плоскости угла помещен кольцевой проводник радиусом 10 см так, что стороны угла являются касательными к нему (рис.3).
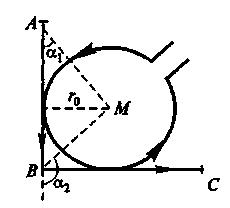
Рис. 3
Найти индукцию в центре кольца. Силы токов в проводнике равны 2А. Влияние проводящих проводов не учитывать.
Дано: 
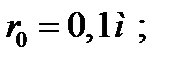
Найти: В.
Решение: Индукция 
в точке поля от элемента любой конфигурации проводника 
с током I, определяется по закону Био-Савара –Лапласа:
(1)
где r- расстояние от элемента до точки, где определяется индукция; 
- угол, составленный векторами 
и r; 
- магнитная постоянная. Направление вектора индукции перпендикулярно плоскости, содержащей и r, и определяется правилом правого винта. Например, в центре окружности (см. рис.) векторы индукции от всех элементов перпендикулярны плоскости окружности и направлены на нас. Интегрируя выражение (1), получаем индукцию в центре окружности радиуса 
: 
.
Индукция, создаваемая в точке М отрезками АВ и ВС и прямого проводника на расстоянии 
от него, равна:
.
