Векторы индукции В2 и В3 в точке М совпадают по направлению с В1. По условию задачи 
, 
и индукция от двух сторон угла составляет:
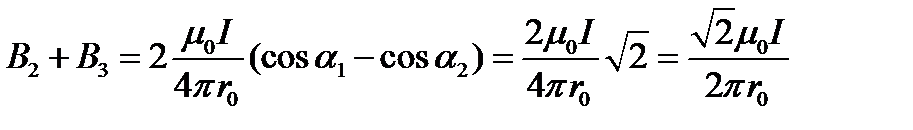
Результирующая индукция в центре кольца равна сумме:
.
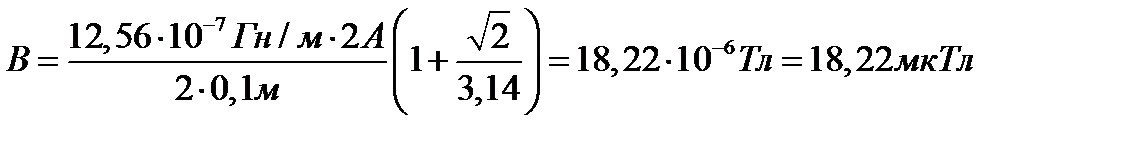Ответ: 
.
26. На рис.4 изображены сечения трех прямолинейных бесконечно длинных проводников с токами. Расстояния АВ=ВС=5см, токи I1=I2=I; I3=2I. Найти точку на прямой АС, в которой напряженность магнитного поля, вызванного токами I1, I2, I3, равна нулю.
Дано: АВ=ВС=а=5см; I1=I2=I; I3=2I.
Найти: r.
|
Рис. 4
Решение: Напряженность Н магнитного поля, созданного каждым из проводников на расстоянии R от проводника, определяется по формуле: 
. С учетом направления токов искомая точка находится на отрезке АВ на расстоянии r от проводника с током I1.
; 
; 
.
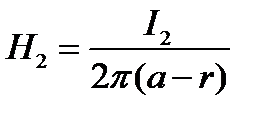Как видно из рис.2, H1+H3=H2.
; 
.
Решая уравнение относительно r, получим r=3,33 см.
Ответ: r =3,33 см.
27. Квадратная рамка со стороной 1 см содержит 100 витков и помещена в однородное магнитное поле напряженностью 100 А/м. Направление поля составляет угол 30° с нормалью к рамке (рис. 5). Какая работа совершается при повороте рамки на 30° в одну и другую сторону, если по ней течет ток 1 А?
Дано: а = 0,04 м; N=100; Н= 100 А/м; αо = 30°; I= 1 А.
Найти: А] и А2.
Решение: При повороте рамки на 30° по часовой стрелке угол α между В и п будет равен 0°, т.е. рамка расположится перпендикулярно полю. При повороте рамки на 30° в другую сторону угол α 2 между В и п будет равен 60°. Работа поворота рамки А=1∆Ф, где I - ток; ∆Ф=Фо-Ф - изменение магнитного потока, пронизывающего плоскость рамки. Ф=ВScosα, где S- площадь рамки, S = а 2;
Рис. 5.
В – индукция магнитного поля,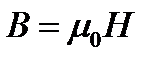 
; μ0 – магнитная постоянная; Н – напряженность магнитного поля.
; 
; 
.
Тогда
;
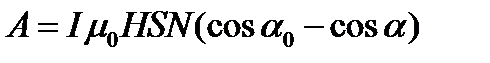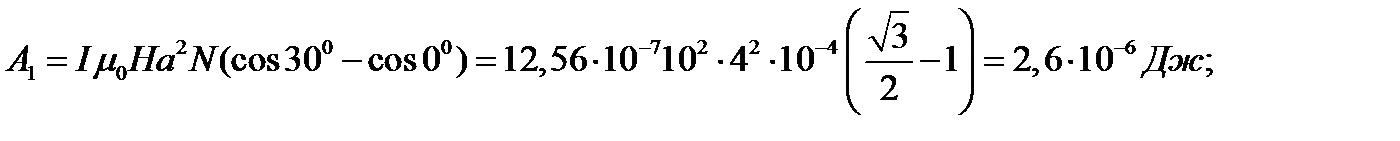
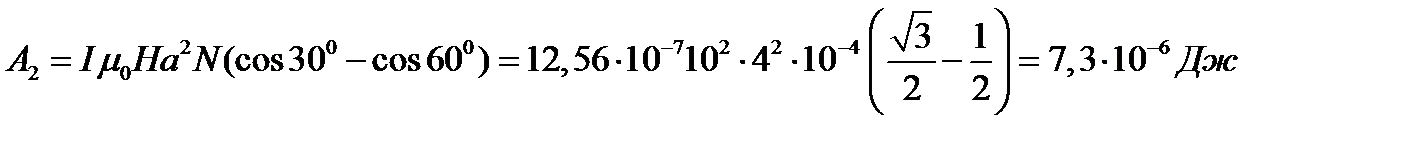
Ответ: 
28. Электрон с энергией 300 эВ движется перпендикулярно линиям индукции однородного магнитного поля напряженностью 465А/м. Определить силу Лоренца, скорость и радиус траектории электрона.
Дано: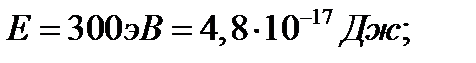 
.
Найти: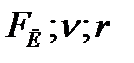 
.
Решение. Кинетическая энергия электрона 
, откуда
.
Сила Лоренца
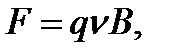
Где q- заряд; В – индукция магнитного поля, 
; μ- магнитная проницаемость среды; μ0 – магнитная постоянная; Н – напряженность поля.
.
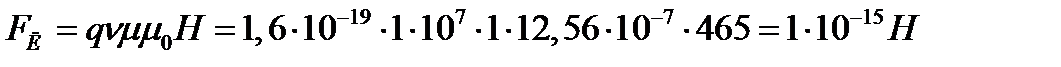В магнитном поле электрон движется по окружности радиуса rпод действием центростремительной силы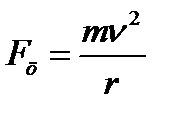 
, численно равной силе Лоренца: 
, тогда
и 
Ответ: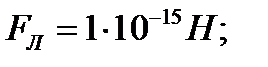 
29. Перпендикулярно линиям индукции однородного магнитного поля индукцией 0,1 мТл по двум параллельным проводникам движется без трения перемычка длиной 20 см (рис. 6). При замыкании цепи, содержащей эту перемычку, в ней идет ток 0,01 А. Определить скорость движения перемычки. Сопротивление цепи 0,1 Ом.
рис. 6
Дано: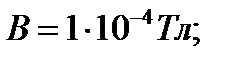 
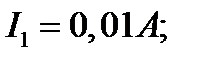
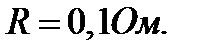
Найти: n.
Решение. Если проводник длиной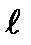 
движется перпендикулярно линиям индукции В магнитного поля со скоростью ν, то на концах его возникает ЭДС индукции εi равная скорости изменения магнитного потока Ф. 
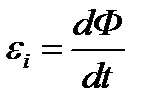. Магнитный поток Ф=ВS, где S - площадь, которую пересекает проводник при своем перемещении (на рис. 6 заштрихована).
/
Если в перемычке с сопротивлением R возникает ток I, значит на концах ее возникла ЭДС, РАВНАЯ 
. Эта ЭДС равна
.
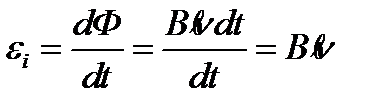Приравнивая правые части этих выражений, получим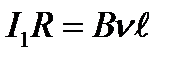 
, откуда
.
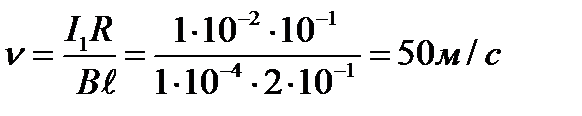Ответ: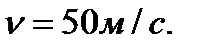 
30. Цепь состоит из соленоида и источника тока. Соленоид без сердечника длиной 15 см и диаметром 4 см имеет плотную намотку из двух слоев медного провода диаметром 0,2 мм. По соленоиду течет ток 1 А. Определить ЭДС самоиндукции в соленоиде в тот момент времени после отключения его от источника, когда сила тока уменьшилась в два раза. Сопротивлением источника и подводящих проводов пренебречь.
Дано: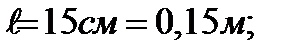 
; 
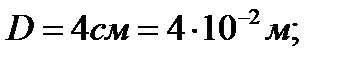
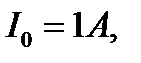
Найти: ε.
Решение. При размыкании цепи сила тока 
, где R и L – сопротивление и индуктивность соленоида. ЭДС самоиндукции 
. В момент t, когда 
, ЭДС самоиндукции 
. Сопротивление провода 
, где ρ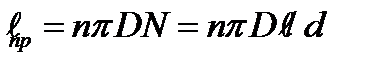 
- длина провода; 
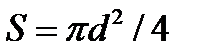- его сечение. Таким образом, 
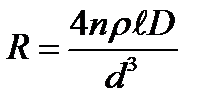, следовательно,
.
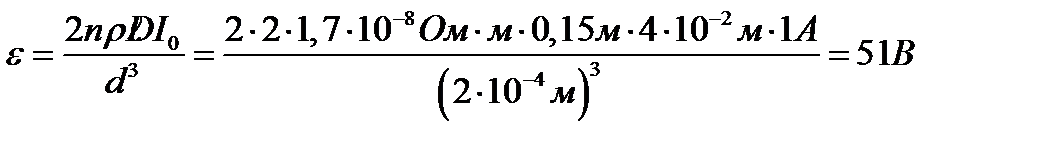Ответ: 
.
31. Соленоид без сердечника имеет плотную однослойную намотку провода диаметром 0,2мм и по нему течет ток 0,1А. Длина соленоида 20 см, диаметр 5 см. Найти энергию и объемную плотность энергии магнитного поля соленоида.
Дано: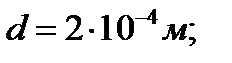 
; 
.
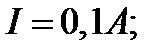
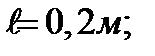
Найти: W, w.
Решение. Энергия магнитного поля соленоида 
, где L- индуктивность соленоида,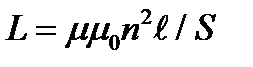 
; 
- магнитная постоянная; n- число витков на 1 м длины соленоида, при плотной намотке 
; 
- длина соленоида; 
-площадь сечения соленоида. Тогда:
Объемная плотность энергии определяется по формуле:
.
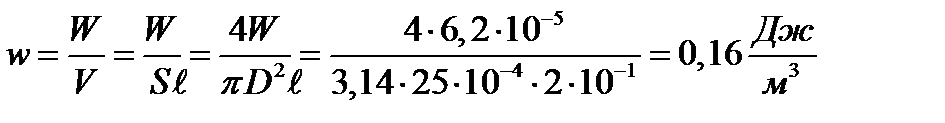Ответ: 
.
32. Материальная точка массой 10 г. совершает гармоническое колебание с периодом 1 с. Амплитуда колебаний равна 5 см. Определить максимальнуюcилу, действующую на точку, и ее полную энергию.
Дано: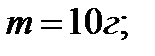 
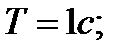
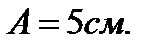
Найти: 
Решение. Уравнение гармонического колебания имеет вид
(1)
где 
- смещение материальной точки от положения равновесия;
- циклическая частота колебаний; ω0 –начальная фаза.
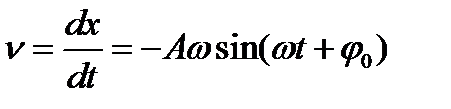(2)
(3)
Согласно второму закону Ньютона, сила, действующая на точку, определяется как
(4)
а ее максимальное значение равно
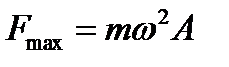
(5)
Полная энергия колеблющейся точки складывается из кинетической и потенциальной энергий и равна максимальной кинетической или максимальной потенциальной энергии. Учитывая, что, согласно (2),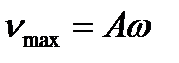 
, находим
(6)
Подставляя в (5) и (6) числовые значения и учитывая, что циклическая частота и период колебаний связаны соотношением 
, получим
;
;
.
Ответ: 
; 
.
33. Конденсатору емкостью 40 мкФ сообщен заряд 0,3 мКл, после чего его замыкают на катушку с индуктивностью 0,1 Гн. Пренебрегая сопротивлением контура, найти законы изменения напряжения на конденсаторе и силы тока в цепи.
Дано: С=40·10-6 Ф; qm=0,3∙10-3 Кл; L=0,1Гн.
Найти: U=U(t); I=I(t)
Решение. В отсутствие омического сопротивления свободные колебания в контуре описываются уравнением
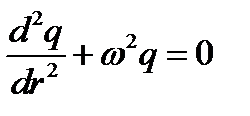, (1)
Где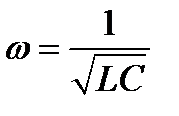 
- циклическая частота колебаний.
Решение уравнения (1) имеет вид
, (2)
где φ0 – начальная фаза колебаний. Поскольку в начальный момент времени (при t=0) заряд конденсатора 
, то 
и, следовательно, 
.
Напряжение на конденсаторе
(3)
а сила тока в цепи
(4)
Подставляя числовые значения, получим
;
.
Таким образом, 
; 
.
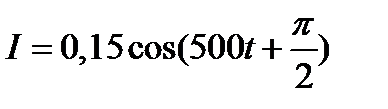Ответ: ; .
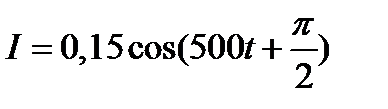34. В однородной изотропной среде с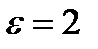 
и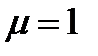 
распространяется плоская электромагнитная волна. За время t=1c энергия, переносимая этой волной через поверхность площадью 1м2, расположенную перпендикулярно направлению распространения волны, равна 1,5 Дж. Найти амплитуды напряженности электрического и магнитного полей волны. Период колебаний 
.
Дано: 
; 
; 
; 
.
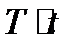Найти: Еm; Нm.
Решение. Плотность потока энергии электромагнитной волны определяется вектором Пойнтинга:
.
Учитывая, что векторы напряженности электрического Е и магнитного Н полей волны взаимно перпендикулярны, для модуля вектора Пойнтинга получим
Р=ЕН.
Поскольку колебания напряженностей Е и Н совершаются в одинаковых фазах, зависимость плотности потока энергии от времени имеет вид
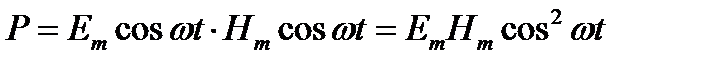(3)
Поток энергии через поверхность S, расположенную перпендикулярно направлению распространения волны, равен
(4)
а для энергии, переносимой волной за время t через эту поверхность, получим выражение
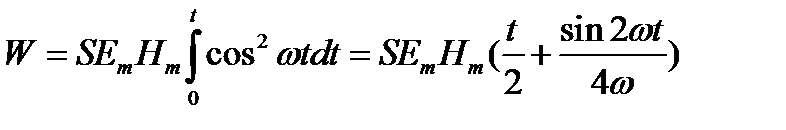(5)
По условию 
, следовательно, 
и выражение (5) принимает вид
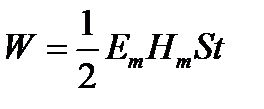(6)
Учитывая, что амплитуды напряженностей электрического и магнитного полей волны связаны соотношением
, (7)
Представим выражение (6) в виде
(8)
; 
(9)
Подставляя числовые значения, получим
;
.
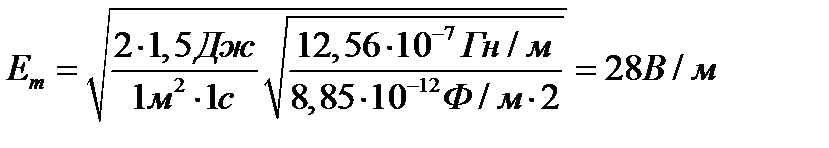Ответ: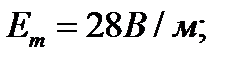 
.
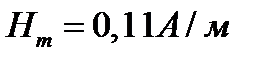35. Найти минимальную толщину пленки с показателем преломления 1,33, при котором свет с длиной волны 0,64 мкм испытывает максимальное отражение, а свет с длиной волны 0,40 мкм не отражается совсем. Угол падения света равен 450.
Дано: 
; 
; 
; 
.
Найти: 
.
Решение. Оптическая разность хода лучей, отраженных от нижней и верхней поверхностей пленки, равна
(1)
Для света с длиной волны 
, имеющего максимальное отражение, выполняется условие 
, т.е.
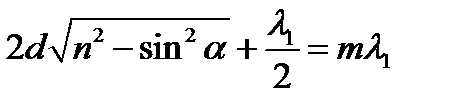(2)
Отсюда 
(3)
Для света с длиной волны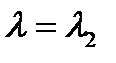 
, не имеющего отражения, 
и, следовательно,
(4)
Из формулы имеем
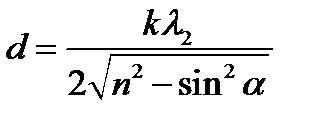(5)
Сравнивая выражения (3) и (5), получаем соотношение
(6)
Из которого следует, что 
и, соответственно,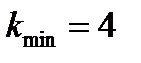 
.
Таким образом,
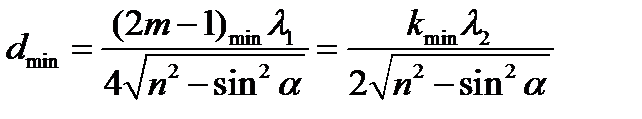(7)
Подставляя числовые значения, получим
.
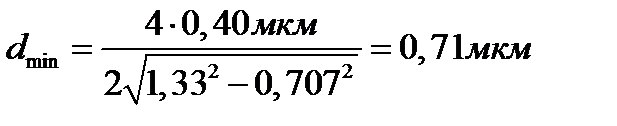Ответ: 
.
36. Между точечным источником света и экраном поместили диафрагму с круглым отверстием, радиус r которого можно менять. Расстояния от диафрагмы до источника и экрана равны 100 и 125 см соответственно. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при 
и следующий максимум при 
.
Дано: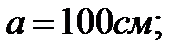 
; 
.
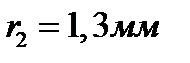Решение. Радиусы зон Френеля определяются выражением
(1)
Следовательно, число зон Френеля, открываемых отверстием радиуса r, равно
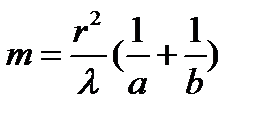(2)
Так как в центре экрана наблюдается максимум освещенности, то число m- нечетное. Для 
имеем
(3)
а для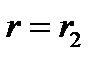 
получим
(4)
Причем по условию 
(5)
Из выражений (3) и (4) с учетом (5) следует, что
(6)
Отсюда
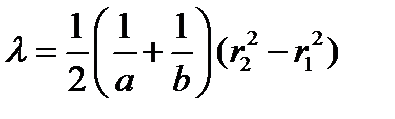(7)
Подставляя числовые значения, получим
.
Ответ: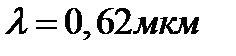 
.
37. При падении естественного света на поляризатор проходит 30% светового потока, а через два таких поляризатора -13,5%. Найти угол между плоскостями пропускания этих поляризаторов.
Дано: 
; 
.
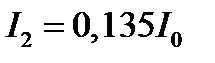Найти: 
.
Решение. Естественный свет можно представить как наложение двух некогерентных волн одинаковой интенсивности, поляризованных во взаимно перпендикулярных плоскостях. Идеальный поляризатор пропускает колебания, происходящие в его плоскости, и полностью задерживает колебания, перпендикулярные этой плоскости. На выходе из первого поляризатора получается линейно поляризованный свет, интенсивность которого с учетом потерь на отражение и поглощение света поляризатором равна
, (1)
где τ – коэффициент, учитывающий потери на отражение и поглощение света.
После прохождения второго поляризатора интенсивность света уменьшается как за счет отражения и поглощения света поляризатором, так как и из-за несовпадения плоскости поляризации света с главной плоскостью поляризатора. В соответствии с законом Малюса и учитывая потери на отражение и поглощение света, имеем
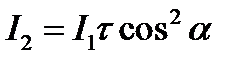(2)
Из (1) найдем
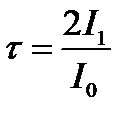(3)
Подставляя (3) и (2), получим
(4)
Отсюда
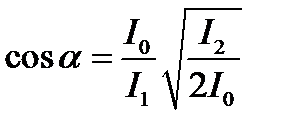(5)
Подставляя числовые данные, получим
.
