 №3.
№3.
 |


Тема 4. №1. а) Гипербола с центром (2;3) и полуосями a = 3, b = 4; б) окружность
с центром (4; - 3) и радиусом 6; в) парабола с вершиной (- 4; 4) и ветвями, направленными вправо; г) эллипс с центром (3; - 1) и полуосями a = 4, b = 2.
№2. (х + 1) 2 + (у – 1) 2 = 5. №3.  + у 2 = 1. №4. х 2 – у 2 = 1. №5. х 2 = - 2 у.
+ у 2 = 1. №4. х 2 – у 2 = 1. №5. х 2 = - 2 у.
№6. (х – 3) 2 + (у – 4) 2 = 25. №7.  + у 2 =
+ у 2 =  С 2. №8.
С 2. №8.  -
-  = 1.
= 1.
Тема 5. №1. N0(ε) =  ; 2; 7; 24. №2. δ (ε) = 2,5ε; 0,25; 0,05.
; 2; 7; 24. №2. δ (ε) = 2,5ε; 0,25; 0,05.
№3. Указание. Воспользоваться определением предела функции по Гейне.
№4. а) 0; б) 0; в) 0,5; г) 0; д) ∞; е) ∞; ё) 9; ж) – 3; з) 1; и) 3; й) 2; к) 0; л) 1,5;
м) 0,25; н) 1,75; о) 2/3; п) 1,5; р) -0,5; с) 1,5. №5. а) 1; б) 3; в) 0,25; г) 0,5; д) 0,5;
е) е 3; ё) е – 4; ж) е – 4; з) 3; и) 4/9; й) е – 1; к) 2,5. №6. 128 / 729.
Тема 6. №1. а) х = 4 – точка разрыва 2-го рода; б) х = 0 – точка разрыва 1-го рода;
в) х = 3 – точка разрыва 2-го рода; г) х = 0 – точка устранимого разрыва;
д) х =  , х =
, х =  - точки разрыва 2-го рода, х =
- точки разрыва 2-го рода, х = 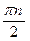 - точки устранимого разрыва, п
- точки устранимого разрыва, п  Z.
Z.
Тема 7. №1. а)  ; б) – 2sin 2 x; в) -
; б) – 2sin 2 x; в) - 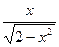 . №2. а) 14 х 6 – 10 х +
. №2. а) 14 х 6 – 10 х +  ; б)
; б) 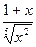 ;
;
в) 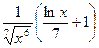 ; г) -
; г) -  ; д) -
; д) -  ; е)
; е)  cos
cos  ; ё)
; ё)  ; ж)
; ж)  ;
;
з) - 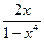 ; и) – ln 3 · sin 2 x ·
; и) – ln 3 · sin 2 x ·  ; й)
; й) 
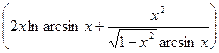 ;
;
к) 
 . №3. у’ =
. №3. у’ =  .
.
№4. 120 х +  + 2 х ln 32. №5. а) sin
+ 2 х ln 32. №5. а) sin  ; б)
; б)  .
.
Тема 8. №1. ∆ у = (6 х 2 + 6 х + 6)∆ х + (6 х + 3)∆ х 2 + 2∆ х 3, d y = (6 х 2 + 6 х + 6)d x.
№2. а) 0,77; б) 2,995.
Тема 9. №1. а)  ; б)
; б) 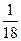 ; в) 0; г) 0; д) ∞; е)
; в) 0; г) 0; д) ∞; е)  ; ё) 1; ж) 1; з) 1.
; ё) 1; ж) 1; з) 1.
Тема 10. №1. х = - 2, у = х – 1, у = - х + 1. №2. Возрастает при х  (- ∞; - 1)
(- ∞; - 1)  (5; + ∞), убывает при х
(5; + ∞), убывает при х  (- 1; 5). №3. х 1 =
(- 1; 5). №3. х 1 =  - точка локального максимума, у (х 1) =
- точка локального максимума, у (х 1) =  ;
;
х 2 = 2 – точка локального минимума, у (х 2) = 0. №4. Выпукл вверх при х  (- ∞; - 2),
(- ∞; - 2),
выпукл вниз при х  (- 2; + ∞); М (- 2; 64) – точка перегиба.
(- 2; + ∞); М (- 2; 64) – точка перегиба.
№5. а)  б)
б) 
в)  г)
г) 
д) 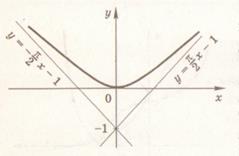
Тема 11. №1. а) х 2 + у 2 < 9 – круг с центром (0; 0) и радиусом 3;
б) | х + у | ≤ 1 – полоса между прямыми х + у = - 1 и х + у = 1.
№2. а) zx' = 2 х + 3  -
-  , zу' =
, zу' = 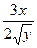 - 1 +
- 1 +  ; б) zx' =
; б) zx' = 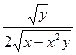 , zу' =
, zу' =  . №3. а)
. №3. а)  = 6 + 2 у,
= 6 + 2 у,  = 2 х + 4 у – 4,
= 2 х + 4 у – 4,  = 4 х – 6 у; б)
= 4 х – 6 у; б)  = -
= -  sin
sin  ,
,
 = -
= -  sin
sin  ,
,  = -
= - 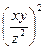 sin
sin  ,
, 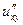 = -
= -  sin
sin  +
+  cos
cos  ,
,
 = -
= -  sin
sin  -
-  cos
cos  ,
,  =
=  sin
sin  -
-  cos
cos  . №4. (4 х – у)d x + (9 у 2 – х)d y.
. №4. (4 х – у)d x + (9 у 2 – х)d y.
№5. 1,509. №6. Увеличится на 10,25%. №7. -  . №8.
. №8.  . №9. Точка М0 лежит
. №9. Точка М0 лежит
на линии уровня х 2 + у 2 = 5, grad z (M0) = - 2 i – 4 j, | grad z (M0) |= 2  .
.
Тема 12. №1. а) min y = y (- 1) = y (1) = 2, max y = y (- 3) = 66; б) min y = y (0) = y (1) = - 4, max y = y (4) = 0. №2. Через 1 неделю. №3. 13. №4. а) М(- 4; 1) – точка минимума,
z (М) = - 1; б) М1(0; 0) – точка минимума, z (М1) = 0, М2(1; 0), М3(- 1; 0) – точки макси-мума, z (М2) = z (М3) =  . №5. min z = z
. №5. min z = z 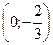 =
=  , max z = z (0; 1) = 7.
, max z = z (0; 1) = 7.
№6. М (- 1,5; - 1,5) – точка минимума, z (М) = - 4,75. №7. (90; 60).
Тема 13. №1. а) 2  -
-  + С; б)
+ С; б)  ln
ln  + C; в) – 2ctg 2 x + C; г) tg x – x + C.
+ C; в) – 2ctg 2 x + C; г) tg x – x + C.
№2. а)  ln | x 2 – 5| + C; б)
ln | x 2 – 5| + C; б) 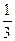 arctg x 3 + C; в) 2
arctg x 3 + C; в) 2  + С; г)
+ С; г)  + С;
+ С;
д)  arcsin
arcsin 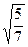 x + C; е)
x + C; е)  arctg
arctg  + C. №3. а) – x cos x + sin x + C; б) x ln x – x + C;
+ C. №3. а) – x cos x + sin x + C; б) x ln x – x + C;
в)  (10 х 2 – 12 х – 1) sin 2 x +
(10 х 2 – 12 х – 1) sin 2 x +  (5 x – 3) cos 2 x + C; г)
(5 x – 3) cos 2 x + C; г)  arctg x -
arctg x - 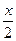 + C;
+ C;
д) – х ctg x + ln |sin x | + C; е) -  + ln
+ ln  + C; ё)
+ C; ё)  (sin x + cos x) е х + С.
(sin x + cos x) е х + С.
№4. а) ln  + C; б) х + 2,5 ln | х 2 – 6 х + 10| + 5 arctg (х – 3)+ С;
+ C; б) х + 2,5 ln | х 2 – 6 х + 10| + 5 arctg (х – 3)+ С;
в) ln  -
-  + arctg x + C; г) ln
+ arctg x + C; г) ln  +
+  arctg x +
arctg x +  + С;
+ С;
д)  ln
ln  +
+  arctg
arctg  + C. №5. а)
+ C. №5. а)  cos 7 x -
cos 7 x -  cos 5 x + C;
cos 5 x + C;
б)  х -
х -  sin 4 x + C; в)
sin 4 x + C; в)  sin 2 x -
sin 2 x -  sin 8 x + C; г) ln
sin 8 x + C; г) ln  + C.
+ C.
№6. а)  +
+  + 3
+ 3 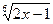 + 3 ln |
+ 3 ln | 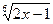 - 1| + C;
- 1| + C;
б)  arcsin
arcsin  +
+  + C; в)
+ C; в)  + С; г)
+ С; г)  arccos
arccos  + C.
+ C.
Тема 14. №1. а) 2  ; б) 4 – 2
; б) 4 – 2  ; в) 1
; в) 1  .
.
Тема 15. №1. а) 1; б)  ; в) расходится; г)
; в) расходится; г) 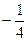 .
.
Тема 16. №1. а) 2  ; б) 6π. №2.
; б) 6π. №2.  . №3.
. №3. 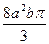 .
.
Тема 17. №1. у = С (х + 1) е – х. №2. у =  . №3.
. №3.  = ln |C x |. №4. (х – 2)2 – у 2 = 4.
= ln |C x |. №4. (х – 2)2 – у 2 = 4.
№5. а) у =  ; б) у =
; б) у =  (х
(х  + arcsin x)
+ arcsin x)  .
.
№6. а) у – 3 = С cos3 x – 3 sin x cos2 x; б) у =  . №7. а) х 3 + 2 ху – 3 у = С;
. №7. а) х 3 + 2 ху – 3 у = С;
б)  + у
+ у  = 2.
= 2.
Тема 18. №1. а) у = - ln |cos x |; б) у = х 3 + 3 х; в) у =  ; г) у = ±
; г) у = ±  .
.
Тема 19. №1. а) у = С1 е х + С2 е – 2 х ; б) у = (С1 + С2 х) е х; в) у = (С1cos 3 x + C2sin 3 x) e 2 x;
г) у = (С1 + С2 х) cos x + (C3 + C4 x) sin x. №2. а) у = С1cos x + C2sin x + (2 х – 2) е х;
б) у = С1 + С2 х + (С3 + х) е – х + х 3 – 3 х 2.
Тема 20. №1. а) сходится; б) расходится; в) расходится; г) сходится; д) сходится;
е) сходится; ё) сходится; ж) сходится; з) сходится. №2. а) сходится условно;
б) сходится условно; в) сходится абсолютно.
Тема 21. №1. а) – 1 < x ≤ 1; б) – 5 ≤ x < 3; в) - ∞ < x < +∞; г) х = 0; д)  ≤ x ≤
≤ x ≤  .
.
Тема 22. №1.  =
=  (- 3 < x < - 1). №2. а)
(- 3 < x < - 1). №2. а) 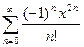 (- ∞ < x < +∞);
(- ∞ < x < +∞);
б) 1 +  (| х | < 1); в)
(| х | < 1); в)  . Указание. Воспользоваться формулой суммы геометрической прогрессии; г)
. Указание. Воспользоваться формулой суммы геометрической прогрессии; г)  (| х | <
(| х | <  ). Указание. Разложить данную дробь
). Указание. Разложить данную дробь
на простейшие. №3. arcsin x = х +  . №4.
. №4.  ln
ln 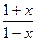 . №5. sin 1 ≈ 0,8417
. №5. sin 1 ≈ 0,8417
с точностью до 0,0002. №6. 0,999848. №7. 3,1416.
Ответы к домашним заданиям.
Тема 1. №1. а) 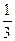 ; б) 0. №2. log 3 4. №3. “+”. №4. D(y) = (0; 2)
; б) 0. №2. log 3 4. №3. “+”. №4. D(y) = (0; 2)  (3; +
(3; + 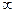 ).
).
№5. tg  = -
= -  , cos
, cos  =
=  , sin
, sin  = -
= -  . №6. а) 2cosec
. №6. а) 2cosec  ; б)
; б) 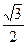 ; в)
; в)  ; г) 1;
; г) 1;
д)  . №7. 9. №8. 4
. №7. 9. №8. 4  .
.
Тема 2. №1. а) – 0,5 + 1,5 i; б) – 1; в) 2  i; г) 8; д)
i; г) 8; д)  + i
+ i  , - 1 + i,
, - 1 + i,
-  - i
- i  ; е) 1 ± i, - 1 ± i. №2. а) ± 2 i; б) 3 ± 3 i; в) 4 ± i, - 4 ± i.
; е) 1 ± i, - 1 ± i. №2. а) ± 2 i; б) 3 ± 3 i; в) 4 ± i, - 4 ± i.
Тема 3. №1. а) Ø; б) (- 5; - 4)  (0; 5); в) (0; 1)
(0; 5); в) (0; 1)  (1; 3). №2. а) (- ∞; 9]; б) [3- 16; + ∞).
(1; 3). №2. а) (- ∞; 9]; б) [3- 16; + ∞).
№3.
 | 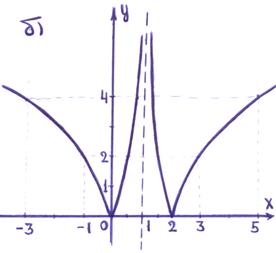 | ||
Тема 4. №1. а) эллипс с центром (2; - 1) и полуосями a = 2, b =  ; б) парабола
; б) парабола
с вершиной (2; - 3) и ветвями, направленными влево; в) окружность с центром
(- 5; 2) и радиусом 4; г) гипербола с центром (- 5; 1) и полуосями a = 8, b = 6.
№2. х 2 + (у – 4) 2 = 16. №3.  +
+  = 1. №4.
= 1. №4.  = 1. №5. у 2 = 4 х.
= 1. №5. у 2 = 4 х.
Тема 5. №1. N0 (ε) =  ; 1; 3; 8. №2. δ (ε) = 2ε; 0,2; 0,06. №4. а) 3; б) 4;
; 1; 3; 8. №2. δ (ε) = 2ε; 0,2; 0,06. №4. а) 3; б) 4;
в) 0,5; г) -  ; д)
; д)  ; е)
; е) 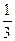 при х → ∞; - 2 при х → - ∞; ё) 1; ж)
при х → ∞; - 2 при х → - ∞; ё) 1; ж)  ; з) – 1; и)
; з) – 1; и)  ;
;
й) – 3; к) 4; л) 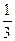 ; м) 6
; м) 6  ; н) 1; о) е – 4; п) е 10; р) – 2; с)
; н) 1; о) е – 4; п) е 10; р) – 2; с)  ; т)
; т)  ; у) -
; у) -  .
.
Тема 6. №1. а) х = 1 – точка разрыва 1-го рода; б) х = - 1 – точка устранимого разрыва, х = 1 – точка разрыва 2-го рода; в) х = πп – точки устранимого разрыва,
х =  + πп – точки разрыва 2-го рода, п
+ πп – точки разрыва 2-го рода, п  Z.
Z.
Тема 7. №1. а)  ; б) 3 х ln 3. №2. а) -
; б) 3 х ln 3. №2. а) -  ; б)
; б)  ; в)
; в)  ;
;
г) 6 ln 2 ·  · x + ctg x; д)
· x + ctg x; д)  ; е)
; е)  + arctg x · x arctg x – 1.
+ arctg x · x arctg x – 1.
№3.  . №4. а) cos
. №4. а) cos  ; б) ln n 2 (2 x + (- 1) n 2 – x ); в)
; б) ln n 2 (2 x + (- 1) n 2 – x ); в)  .
.
Тема 8. №1. 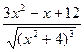 е 3 х – 5 d x. №2. а) 1,077; б) 1,0349.
е 3 х – 5 d x. №2. а) 1,077; б) 1,0349.
Тема 9. №1. а) 2; б) 0,5; в) 1; г)  ; д) 3; е)
; д) 3; е)  .
.
Тема 10. №1. у = 2 х +  при х → + ∞, у = 2 х -
при х → + ∞, у = 2 х -  при х → - ∞. №2. Возрастает при
при х → - ∞. №2. Возрастает при
х  (- 2; 0), убывает при х
(- 2; 0), убывает при х  (0; 2). №3. уmax
(0; 2). №3. уmax 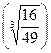 = 0,2. №4. Выпукла вниз при
= 0,2. №4. Выпукла вниз при
х  (- ∞; -
(- ∞; -  )
)  (1; + ∞), выпукла вверх при х
(1; + ∞), выпукла вверх при х  (-
(-  ; 0)
; 0)  (0; 1), х = -
(0; 1), х = -  - точка перегиба, в точке х = 0 перегиба нет.
- точка перегиба, в точке х = 0 перегиба нет.
 №5. а)
№5. а)  б)
б) 
в)  г)
г)
Тема 11. №1. х 2 + у 2 > 4 – внешность круга с центром (0; 0) и радиусом 2.
№2. их ' = -  , иy ' = -
, иy ' = -  ,
,
иz ' =  . №3. 9,36. №4.
. №3. 9,36. №4.  . №5. grad z (M0) = 0,3 i,
. №5. grad z (M0) = 0,3 i,
| grad z (M0) |= 0,3.
Тема 12. №1. min y = y  = - 9,75, max y = y (8) = 24. №2. 0,3 м; V = 0,486 м 3. №3.
= - 9,75, max y = y (8) = 24. №2. 0,3 м; V = 0,486 м 3. №3.  .
.
№4. а) М(1; 2) – точка минимума, z (М) = - 7; б) М 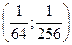 - точка максимума,
- точка максимума,
z (М) = 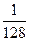 . №5. z min
. №5. z min  = ln (4 -
= ln (4 -  ), z max
), z max 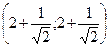 = ln (4 +
= ln (4 +  ).
).
№6. z min (1; 1) = 2. №7. (0; 500).
Тема 13. №1. а)  -3 х + 6
-3 х + 6  - ln | x | + C; б) 5 tg x + 2 ctg x + C; в)
- ln | x | + C; б) 5 tg x + 2 ctg x + C; в)  + С;
+ С;
г) 2  +
+  ln 2 x + С; д)
ln 2 x + С; д)  + С; е) arcsin
+ С; е) arcsin  + C; ё) х arcsin x +
+ C; ё) х arcsin x +  + C;
+ C;
ж) (х 2 – 2) sin x + 2 x cos x + C; з)  х 2 +
х 2 +  х sin 2 x +
х sin 2 x +  cos 2 x + C; и)
cos 2 x + C; и) 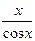 - ln
- ln  ;
;
й)  е х (sin x – cos x) + C; к) 5 х + ln
е х (sin x – cos x) + C; к) 5 х + ln  + C; л)
+ C; л) 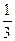 х 3 + х 2 – х +
х 3 + х 2 – х + 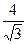 arctg
arctg  + C;
+ C;
м) 3 ln  + 2 arctg
+ 2 arctg  + C; н)
+ C; н)  +
+  + 2 ln
+ 2 ln  + C;
+ C;
о)  +
+  arctg
arctg 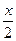 + C; п)
+ C; п)  ln
ln  +
+  arctg
arctg 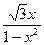 + C;
+ C;
р)  +
+ 
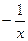 - arctg x + С; с)
- arctg x + С; с)  cos 8
cos 8 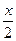
 cos 6
cos 6 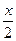 + C; т)
+ C; т) 
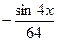 +
+  ;
;
у)  +
+ 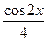 + С; ф)
+ С; ф)  sin
sin  + 3 sin
+ 3 sin  + C; х)
+ C; х)  ln
ln  + C;
+ C;
ц) – 2 arctg  + C; ч)
+ C; ч)  + С; ш) 2 arcsin
+ С; ш) 2 arcsin 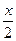
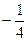 x (2 – x 2)
x (2 – x 2)  + C;
+ C;
щ) arcsin  + C.
+ C.
Тема 14. №1. а) 33 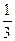 ; б)
; б)  ; в)
; в)  (4
(4  - 3) – ln
- 3) – ln  .
.
Тема 15. №1. а) π; б) расходится.
Тема 16. №1. а) 20  ; б) π. №2.
; б) π. №2.  . №3.
. №3.  .
.
Тема 17. №1. а) ln | x | = C + 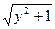 ; б) 2
; б) 2  = 1 + е х; в) у = С
= 1 + е х; в) у = С  ; г) у = х
; г) у = х  ;
;
д) у = х (С + sin x); е) у =  ; ж) у (е х + С е 2 х ) = 1; з) х 3 у – 2 х 2 у 2 + 3 у 4 = С.
; ж) у (е х + С е 2 х ) = 1; з) х 3 у – 2 х 2 у 2 + 3 у 4 = С.
Тема 18. №1. а) у = 3 ln x + 2 х 2 – 6 х + 6; б) у =  х 2; в) 2 у 2 – 4 х 2 = 1.
х 2; в) 2 у 2 – 4 х 2 = 1.
Тема 19. №1. а) у = С1 е 2 х + е – х (С2cos  x + C3sin
x + C3sin  x); б) у = С1 е х + С2 е – х + С3cos x +
x); б) у = С1 е х + С2 е – х + С3cos x +
+ C4sin x; в) у = С1 + С2 х + С3 х 2 + е 3 х (С4 + С5 х); г) у = С1 е х + С2 е – х + С3 е 2 х + С4 е – 2 х ;
д) у = (С1 + С2 х) е – 2 х +  е 2 х ;
е 2 х ;
е) у = С1cos x + C2sin x + C3cos 2 x + C4sin 2 x  x cos x.
x cos x.
Тема 20. №1. а) расходится; б) расходится; в) сходится условно; г) расходится;
д) сходится абсолютно; е) расходится; ё) сходится; ж) расходится; з) сходится.
Тема 21. №1. а) – 1 ≤ х < 1; б) 2 ≤ х < 3; в)  ≤ х ≤
≤ х ≤  .
.
Тема 22. №1. cos 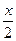 =
=  . №2. а) 2
. №2. а) 2  ;
;
б)  х п (| х | < 1). №3. arctg x =
х п (| х | < 1). №3. arctg x =  х 2 п + 1. №4.
х 2 п + 1. №4.  (| х | < 1).
(| х | < 1).
№5. 1 +  ln (1 – х) (| х | < 1). №6. а) 0,607; б) 0,158.
ln (1 – х) (| х | < 1). №6. а) 0,607; б) 0,158.






