а) Свойства функций.
№1. Найти области определения функций:
а) f (x) =  ; б) f (x) =
; б) f (x) =  ; в) f (x) =
; в) f (x) =  + 3arccos
+ 3arccos  ;
;
г) f (x) = log 2(2 – x) + 2log x 5; д) f (x) = log 0,5 log 3 x.
№2. Найти множества значений функций:
а) f (x) = | х + 1| - 3; б) f (x) =  ; в) f (x) =
; в) f (x) =  .
.
б) Преобразование графиков.
№3. Построить графики функций:
а) у = - 2  ; б) у = х 2 - 5| х | + 6; в) у = |2(х – 1)2 - 4| х - 1| - 16| + 3; г) у =
; б) у = х 2 - 5| х | + 6; в) у = |2(х – 1)2 - 4| х - 1| - 16| + 3; г) у =  .
.
Тема 4. Кривые 2-го порядка.
а) Задачи на построение кривых.
№1. Построить кривые:
а) 16 х 2 – 9 у 2 – 64 х + 54 у – 161 = 0; б) х 2 + у 2 – 8 х + 6 у – 11 = 0;
в) у 2 – 8 у – 4 х = 0; г) х 2 + 4 у 2 – 6 х + 8 у – 3 = 0.
б) Задачи на составление уравнений.
№2. Составить уравнение окружности, проходящей через точки М1(1; 2), М2(0; - 1),
М3(- 3; 0).
№3. Составить каноническое уравнение эллипса, проходящего через точки М1  ,
,
М2  .
.
№4. Написать каноническое уравнение гиперболы, симметричной относительно осей координат, если она проходит через точку М1( ;
;  ), а эксцентриситет равен
), а эксцентриситет равен  .
.
№5. Написать уравнение параболы, если она проходит через точки пересечения пря-
мой х + у = 0 и окружности х 2 + у 2 + 4 у = 0 и симметрична относительно оси Оу.
№6. Составить уравнение окружности, проходящей через точки М1(7; 7), М2(- 2; 4), если её центр лежит на прямой 2 х – у – 2 = 0.
№7*. Написать уравнение эллипса, если расстояние между фокусами равно расстоя-нию между концами большой и малой осей.
№8. Составить уравнение гиперболы, если её асимптоты заданы уравнениями у = ±  х
х
и гипербола проходит через точку М(10; - 3  ).
).
Тема 5. Пределы.
а) Определения пределов.
№1. Доказать, что  . Определить, начиная с какого номера члены данной последовательности будут отличаться от её предела на величину, меньшую
. Определить, начиная с какого номера члены данной последовательности будут отличаться от её предела на величину, меньшую
ε = 0,1; 0,01; 0,001.
№2. Доказать, что  = - 1. Определить, на какую величину
= - 1. Определить, на какую величину  должен отличаться аргумент х от - 1, чтобы данная функция отличалась от своего предела на величину, меньшую чем ε = 0,1; 0,02.
должен отличаться аргумент х от - 1, чтобы данная функция отличалась от своего предела на величину, меньшую чем ε = 0,1; 0,02.
№3. Доказать, что  не существует.
не существует.
б) Алгебраические приёмы раскрытия неопределённостей.
№4. Вычислить: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е) 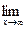 (2 х 5 – 10 х 3 – 1); ё)
(2 х 5 – 10 х 3 – 1); ё)  ;
;
ж)  ; з)
; з)  ; и)
; и)  ; й)
; й)  ; к)
; к)  ; л)
; л)  ; м)
; м)  ;
;
н)  ; о)
; о)  ; п)
; п)  ;
;
р)  ; с)
; с)  .
.
в) Замечательные пределы.
№5. Вычислить: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ; ё)
; ё)  ; ж)
; ж)  ;
;
з)  ; и)
; и)  ; й)
; й)  ; к)
; к)  .
.
г) Вычисление пределов с помощью эквивалентностей.
№6. Вычислить:  .
.
Тема 6. Непрерывность функции.
№1. Исследовать на непрерывность функции:
а) у =  ; б) у = 3 -
; б) у = 3 -  ; в) у =
; в) у =  ; г) у =
; г) у =  ; д*) у =
; д*) у =  .
.
Тема 7. Производная функции.
а) Вычисление производных с помощью определения.
№1. Используя определение, найти производные функций:
а) у =  ; б) у = cos 2 x; в) у =
; б) у = cos 2 x; в) у =  .
.
б) Практикум по вычислению производных.
№2. Найти производные функций:
а) у = 2 х 7 – 5 х 2 + 2  + 1; б) у =
+ 1; б) у =  +
+  ; в) у =
; в) у =  ln x; г) у =
ln x; г) у =  - arctg x;
- arctg x;
д) у =  ; е) у = sin
; е) у = sin  ; ё) у =
; ё) у =  arcsin
arcsin  +
+  ; ж) у = ln (х +
; ж) у = ln (х +  );
);
з) у = ln  ; и) у =
; и) у =  ; й) у =
; й) у =  ; к) у =
; к) у = 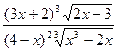 .
.
в) Производная неявной функции.
№3. Найти производную у’x, если ух + log 2(х 2 + у 2) – sin (ху) = 0.
г) Производные высших порядков.
№4. Найти производную у’’’, если у = 5 х 4 -  + 2 х .
+ 2 х .
№5. Найти производные п -го порядка: а) у = sin x; б) у = ln x.
Тема 8. Дифференциал.
№1. Найти полное приращение функции у = 2 х 3 + 3 х 2 + 6 х и её дифференциал, сравнить их.
№2. Найти приближённые значения: а) arctg 0,97; б)  .
.
Тема 9. Вычисление пределов с помощью производной.
№1. Вычислить пределы: а)  ; б)
; б)  ; в)
; в)  ;
;
г)  ; д)
; д)  ; е)
; е)  ; ё)
; ё)  ;
;
ж)  ; з)
; з)  .
.
Тема 10. Исследование функций.
а) Исследование по отдельным факторам.
№1. Найти асимптоты кривой у = 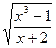 .
.
№2. Найти интервалы монотонности функции у = х 3 – 6 х 2 – 15 х + 2.
№3. Найти экстремумы функции у = х  .
.
№4. Найти интервалы выпуклости и точки перегиба графика функции
у = 0,5 х 3 + 3 х 2 – 18 х + 20.
б) Полное исследование.
№5. Построить графики функций:
а) у =  ; б) у = 3
; б) у = 3  - х; в) у = х 2
- х; в) у = х 2  ; г) у =
; г) у =  х ln
х ln  ; д) х arctg х.
; д) х arctg х.
Тема 11. Функции многих переменных.
а) Область определения.
№1. Найти области определения функций и изобразить их графически:
а) z =  ; б) z = arcsin (х + у).
; б) z = arcsin (х + у).
б) Частные производные.
№2. Найти частные производные функций: а) z = х 2 + 3 х  - у +
- у +  ; б) z = arcsin
; б) z = arcsin  .
.
№3. Найти вторые частные производные функций:
а) z = 3 х 2 + 2 ху 2 – 4 ху + х 2 у – у 3; б) и = sin  .
.
в) Дифференциал.
№4. Записать дифференциал функции z = 2 х 2 – ху + 3 у 3.
№5. Вычислить с помощью дифференциала приближённое значение  .
.
№6. Вычислить, на сколько процентов приближённо изменится спрос, описываемый
функцией q = 5474  , где п – число производителей товара, р – цена товара, если
, где п – число производителей товара, р – цена товара, если
число производителей товара уменьшится на 1, а цена возрастёт на 1%. На рынке
имеется 7 производителей, цена товара составляет 3 единицы.
г) Производная по направлению.
№7. Найти производную функции z = х 3 у – 5 ху 2 + 8 по направлению вектора l = {1; 1}
в точке М (1; 1).
№8. Найти производную функции и = ln (x 2 + y 2 + z 2) в точке М (1; 2; 1) по направле-
нию вектора MN, где N (3; 6; 5).
№9. Построить линии уровня функции z = 4 – х 2 – у 2. Найти градиент функции z в то-
чке М0 (1; 2) и его модуль.
Тема 12. Экстремальные задачи.
а) Наибольшее и наименьшее значения функции одной переменной.
№1. Найти наименьшее и наибольшее значения функций:
а) у = х 4 – 2 х 2 + 3 на отрезке [- 3; 2]; б) у = х 2 – 2 х  + х – 4 на отрезке [0; 4].
+ х – 4 на отрезке [0; 4].
№2. Если собрать урожай в начале августа, то с каждой сотки можно получить 200 кг
раннего картофеля и реализовать его по 12 руб. за килограмм. Отсрочка уборки на каждую неделю ведёт к увеличению урожайности на 50 кг с одной сотки, но цена
картофеля за килограмм при этом падает на 2 руб. Когда следует собрать картофель,
чтобы доход от его продажи был максимальным, если срок уборки составляет 5 недель?
№3. Издержки производства некоторого товара равны С = 4 + 15 q, спрос на товар определяется функцией р = - q 2 + 20 q + 2; 10 < q < 20. Найти объём продукции q, макси-
мизирующий прибыль.
б) Экстремумы функций многих переменных.
№4. Найти экстремумы функций:
а) z = х 2 – ху + у 2 + 9 х – 6 у + 20; б) z = (2 х 2 + у 2)  .
.
в) Наибольшее и наименьшее значения функции нескольких переменных.
№5. Найти наименьшее и наибольшее значения функции z = 3 х 2 – х 3 + 3 у 2 + 4 у
в области х 2 + у 2 ≤ 1.
г) Условный экстремум.
№6. Найти условные экстремумы функции z = х 2 + у 2 – ху + х + у – 4 при х + у + 3 = 0.
№7. Предприниматель решил выделить на расширение своего дела 150 тыс. руб. Из-
вестно, что если на приобретение нового оборудования затратить х тыс. руб., а на
зарплату вновь принятых работников у тыс. руб., то прирост объёма продукции соста-вит Q = 0,001 х 0,6 у 0,4. Как следует распределить выделенные денежные ресурсы, чтобы
прирост объёма продукции был максимальным?
Тема 13. Неопределённый интеграл.
а) Непосредственное интегрирование.
№1. Найти интегралы: а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
б) Метод замены переменной.
№2. Найти интегралы:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ; е)
; е)  .
.
в) Интегрирование по частям.
№3. Найти интегралы: а)  ; б)
; б)  ; в)
; в) 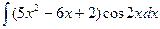 ;
;
г)  arctg x d x; д)
arctg x d x; д)  ; е)
; е)  ; ё)
; ё)  d x.
d x.
г) Интегрирование рациональных дробей.
№4. Найти интегралы: а)  ; б)
; б)  ;
;
в)  ; г)
; г)  ; д)
; д)  .
.
д) Интегрирование тригонометрических выражений.
№5. Найти интегралы:
а)  sin 3 x d x; б)
sin 3 x d x; б)  sin 2 x d x; в)
sin 2 x d x; в)  ; г)
; г)  .
.
е) Интегрирование иррациональных выражений.
№6. Найти интегралы:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Тема 14. Определённый интеграл.
№1. Вычислить интегралы: а)  d x; б)
d x; б)  ; в)
; в)  d x.
d x.
Тема 15. Несобственные интегралы.
№1. Вычислить интегралы или установить их расходимость:
а)  ; б)
; б) 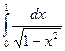 ; в)
; в) 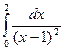 ; г)
; г)  ln x d x.
ln x d x.
Тема 16. Геометрические приложения определённого интеграла.
а) Площади фигур.
№1. Вычислить площади фигур, ограниченных линиями:
а) у = х 2, у = 2 – х 2; б)  +
+  = 1.
= 1.
б) Объёмы тел вращения.
№2. Вычислить объём тела, образованного вращением вокруг оси Ох фигуры, ограни-
ченной линиями у 2 = 9 х, у = 3 х.
№3. Вычислить объём тела, образованного вращением вокруг оси Оу фигуры, ограни-
ченной линиями 
 = 1, у = ± b.
= 1, у = ± b.
Тема 17. Дифференциальные уравнения первого порядка.
а) Уравнения с разделяющимися переменными.
№1. Решить уравнение xy d x + (x + 1) d y = 0.
№2. Решить уравнение (х 2 – 1) у’ + 2 ху 2 = 0 и найти частное решение, удовлетворяющее
начальному условию у (0) = 1.
б) Однородные уравнения.
№3. Решить уравнение ху’ = у - х  .
.
№4. Решить задачу Коши: (х 2 + у 2) d x – 2 xy d y = 0, y (4) = 0.
в) Линейные уравнения.
№5. Решить уравнения и, где указано начальное условие, найти частное решение:
а) х 2 у’ + ху + 1 = 0; б) у’  - 1 – х = 0, у (0) = 0.
- 1 – х = 0, у (0) = 0.
г) Уравнения Бернулли.
№6. Решить уравнения и, где указано начальное условие, найти частный интеграл:
а) у’ = у 4cos x + y tg x; б) (1 – х 2) у’ + 2 ху = ху 2, у (0) = 0,5.
д) Уравнения в полных дифференциалах.
№7. Решить уравнения и, где указано начальное условие, найти частный интеграл:
а) (3 х 2 + 2 у) d x + (2 x – 3) d y = 0; б)  d x +
d x +  d y = 0, у (0) = 2.
d y = 0, у (0) = 2.
Тема 18. Уравнения высших порядков, допускающие понижение порядка.
№1. Решить уравнения и, где указаны начальные условия, найти частный интеграл:
а) у’’ =  , у
, у  =
=  , у’
, у’  = 0; б) (1 + х 2) у’’ – 2 ху’ = 0, у (0) = 0, у’ (0) = 3;
= 0; б) (1 + х 2) у’’ – 2 ху’ = 0, у (0) = 0, у’ (0) = 3;
в) у’’ + 2 уу’ = 0, у (0) = 2, у’ (0) = - 4; г) уу’’ + (у’) 2 = 0.
Тема 19. Линейные уравнения высших порядков с постоянными коэффициентами.
а) Однородные уравнения.
№1. Найти общие решения уравнений:
а) у’’ + у’ – 2 у = 0; б) у’’ - 2 у’ + у = 0; в) у’’ - 4 у’ + 13 у = 0; г) у (4) + 2 у’’ + у = 0.
б) Неоднородные уравнения.
№2. Найти общие решения уравнений:
а) у’’ + у = 4 хе х; б) у’’’ + у’’ = 6 х + е – х.
Тема 20. Числовые ряды.
а) Знакоположительные ряды.
№1. Исследовать ряды на сходимость: а)  ; б)
; б)  ; в)
; в)  ;
;
г) 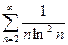 ; д)
; д)  ; е)
; е)  ; ё)
; ё)  ; ж)
; ж)  ; з)
; з)  .
.
б) Знакопеременные ряды.
№2. Исследовать ряды на абсолютную и условную сходимости:
а) 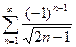 ; б)
; б)  ; в)
; в)  .
.
Тема 21. Степенные ряды.
№1. Определить области сходимости степенных рядов:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
Тема 22. Ряды Тейлора и Маклорена.
а) Разложение функций в ряд Тейлора.
№1. Разложить функцию у =  в ряд Тейлора по степеням (х + 2).
в ряд Тейлора по степеням (х + 2).
б) Разложение функций в ряды Маклорена с помощью основных разложений.
№2. Разложить функции в ряды Маклорена: а)  ; б) cos 2 x; в)
; б) cos 2 x; в)  ; г)
; г)  .
.






