 ,
,
откуда  . Выберем в качестве решения последнего уравнения
. Выберем в качестве решения последнего уравнения  , тогда
, тогда  , и общий интеграл исходного уравнения имеет вид
, и общий интеграл исходного уравнения имеет вид 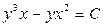 .
.
Задания для самостоятельного решения.
3.26.  .
.
3.27.  .
.
3.28.  . 3.29.
. 3.29.  .
.
3.30.  . 3.31.
. 3.31.  .
.
Ответы
3.26.  . 3.27.
. 3.27. 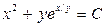 . 3.28.
. 3.28.  .
.
3.29.  . 3.30.
. 3.30.  . 3.31.
. 3.31. 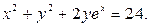
3.3.Дифференциальные уравнения высших порядков, допускающие понижения порядка
Дифференциальное уравнение  го порядка имеет следующий общий вид
го порядка имеет следующий общий вид
 .
.
Его общее решение  содержит две произвольные постоянные
содержит две произвольные постоянные  и
и  .
.
Рассмотрим несколько типов уравнений второго порядка, допускающих понижение порядка.
I. Простейший частный случай уравнения 2-го порядка записывается так: 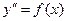 . Искомая функция здесь находится последовательным двукратным интегрированием.
. Искомая функция здесь находится последовательным двукратным интегрированием.
3.8).  . Запишем это уравнение в виде
. Запишем это уравнение в виде  . Умножая обе его части на
. Умножая обе его части на  , имеем
, имеем  . И после интегрирования
. И после интегрирования 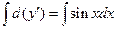 , получаем
, получаем 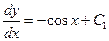 , где
, где  - произвольная постоянная. После умножения обеих частей последнего равенства на
- произвольная постоянная. После умножения обеих частей последнего равенства на  и интегрирования получаем общее решения данного уравнения
и интегрирования получаем общее решения данного уравнения  . Здесь
. Здесь  - вторая произвольная постоянная.
- вторая произвольная постоянная.
II. Уравнение не содержит искомой функции:  . Порядок такого уравнения может быть понижен заменой, введением новой искомой функции
. Порядок такого уравнения может быть понижен заменой, введением новой искомой функции  .
.
3.9). Найти общее решение уравнения:  .
.
Решение. Обозначим 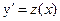 . Тогда
. Тогда 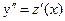 , и данное уравнение теперь выглядит так:
, и данное уравнение теперь выглядит так:
 ,
,
т.е. благодаря используемой здесь замене удалось исходное уравнение второго порядка преобразовать к дифференциальному уравнению первого порядка, добиться понижения порядка исходного уравнения. Разделяя переменные и интегрируя, из последнего равенства получаем:  , т.е.
, т.е.  , а, значит,
, а, значит,  . Разделение переменных и интегрирование последнего равенства дает общее решение исходного уравнения:
. Разделение переменных и интегрирование последнего равенства дает общее решение исходного уравнения:  .
.
III. Уравнение не содержит независимой переменной  :
:  . Рассматривая
. Рассматривая  здесь как независимую переменную, можем на единицу понизить порядок уравнения введением в него новой искомой функции
здесь как независимую переменную, можем на единицу понизить порядок уравнения введением в него новой искомой функции  . При этом
. При этом  .
.
3.10). Решить уравнение:  .
.
Решение. Пользуясь только что указанной подстановкой, понизим порядок данного уравнения: 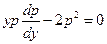 , или
, или  . Отсюда получаем два уравнения:
. Отсюда получаем два уравнения:
 ,
,  .
.
Первое из них дает 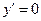 , т.е.
, т.е. 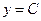 . Второе уравнение решается разделением переменных, откуда
. Второе уравнение решается разделением переменных, откуда 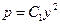 . Но, так как
. Но, так как 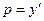 , то, разделяя переменные, получаем
, то, разделяя переменные, получаем  , т.е.
, т.е.  , или
, или  . Отметим, что найденное ранее решение
. Отметим, что найденное ранее решение 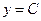 содержится в предыдущей функции при
содержится в предыдущей функции при  .
.
Задания для самостоятельного решения.
3.32.  . 3.33.
. 3.33.  . 3.34.
. 3.34.  3.35.
3.35. 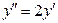 .
.
3.36.  . 3.37.
. 3.37. 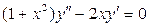 . 3.38.
. 3.38. 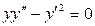 .
.
3.39. 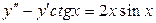 . 3.40.
. 3.40. 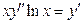 . 3.41.
. 3.41.  . 3.42.
. 3.42. 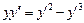
3.43.  . 3.44.
. 3.44. 
.
Ответы
3.32.  . 3.33.
. 3.33.  . 3.34.
. 3.34.  .
.
3.35.  . 3.36.
. 3.36.  ,
,  . 3.37.
. 3.37. 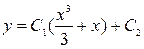 .
.
3.38. 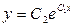 . 3.39.
. 3.39.  .
.
3.40.  . 3.41.
. 3.41.  . 3.42.
. 3.42.  .
.
3.43.  . 3.44.
. 3.44.  .
.
3.4.Линейные дифференциальные уравнения.
Линейным дифференциальным уравнением  го порядка называется уравнение, линейное относительно неизвестной функции и всех ее производных, оно имеет следующий общий вид:
го порядка называется уравнение, линейное относительно неизвестной функции и всех ее производных, оно имеет следующий общий вид:
 (3.22)
(3.22)
Если заданные коэффициенты  и правая часть
и правая часть 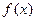 - функции, непрерывные на некотором интервале
- функции, непрерывные на некотором интервале  , то уравнение (3.22) имеет единственное решение
, то уравнение (3.22) имеет единственное решение  , определенное на интервале
, определенное на интервале  и удовлетворяющее начальным условиям
и удовлетворяющее начальным условиям
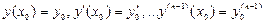 , (3.23)
, (3.23)
где  , а
, а 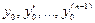 - любые действительные числа.
- любые действительные числа.
Уравнение (3.22), в котором  тождественно на
тождественно на  , называется линейным неоднородным дифференциальным уравнением (ЛНДУ), а уравнение
, называется линейным неоднородным дифференциальным уравнением (ЛНДУ), а уравнение
 (3.24)
(3.24)
- линейным однородным дифференциальным уравнением (ЛОДУ).
Общее решение уравнения (3.24) имеет вид
 , (3.25)
, (3.25)
где 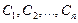 - произвольные постоянные, а
- произвольные постоянные, а  -
-  линейно независимых частных решений уравнения (3.24), составляющих так называемую фундаментальную систему решений ЛОДУ.
линейно независимых частных решений уравнения (3.24), составляющих так называемую фундаментальную систему решений ЛОДУ.
Критерием (т.е. необходимым и достаточным условием) линейной независимости  частных решений
частных решений  уравнения (3.24) является условие необращения в ноль на интервале
уравнения (3.24) является условие необращения в ноль на интервале  определителя Вронского для этих функций:
определителя Вронского для этих функций:


 (3.26)
(3.26)
Общее решение ЛНДУ (3.22) имеет следующий вид:
 . (3.27)
. (3.27)
Здесь 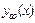 - общее решение ЛОДУ (3.24), соответствующего данному ЛНДУ (3.22), а
- общее решение ЛОДУ (3.24), соответствующего данному ЛНДУ (3.22), а 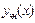 - некоторое частное решение ЛНДУ (3.22). Представление (3.27) вместе с формулой (3.25) описывает структуру общего решения ЛНДУ.
- некоторое частное решение ЛНДУ (3.22). Представление (3.27) вместе с формулой (3.25) описывает структуру общего решения ЛНДУ.
Линейные однородные уравнения с постоянными коэффициентами
Линейное однородное уравнение второго порядка с постоянными коэффициентами выглядит так:
 . (3.28)
. (3.28)
Здесь коэффициенты  и
и  - некоторые действительные числа.
- некоторые действительные числа.
Определим значение параметра  так, чтобы функция
так, чтобы функция  удовлетворяла равенству (3.28), т.е. являлась решением этого уравнения. Для этого подставим эту функцию и ее производные
удовлетворяла равенству (3.28), т.е. являлась решением этого уравнения. Для этого подставим эту функцию и ее производные  ,
, 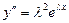 в равенство (3.28). Получим
в равенство (3.28). Получим  , откуда выводим равенство
, откуда выводим равенство
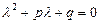 , (3.29)
, (3.29)
называемое характеристическим уравнением линейного однородного дифференциального уравнения (3.28). Уравнение (3.29) является квадратным уравнением и имеет 2 корня (действительных различных, действительных равных, или 2 комплексно - сопряженных). Каждому корню  этого уравнения соответствует отдельное частное решение
этого уравнения соответствует отдельное частное решение 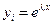 ,
,  В совокупности этот набор решений составляет фундаментальную систему решений уравнения (3.28), с помощью которой по формуле (3.25) можно записать общее решение этого уравнения.
В совокупности этот набор решений составляет фундаментальную систему решений уравнения (3.28), с помощью которой по формуле (3.25) можно записать общее решение этого уравнения.
Таким образом, алгеброй определяется характер решений линейных дифференциальных уравнений, а, значит, и те физические, химические, и.т.д. процессы, которые ими описываются.
Возможные при решении уравнения (3.28) случаи представлены в следующей таблице.
Таблица 2.
| № | Корни характеристического уравнения 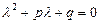
| Фундаментальная система решений диффер. уравнения (3.29) | Вид общего решения уравнения
|
 и и  - действительные различные числа - действительные различные числа
|  , , 
| 
| |
 - двукратный корень - двукратный корень
|  , , 
| 
| |
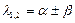 - комплексно сопряженные корни - комплексно сопряженные корни
|  , ,

|

|
3.11). Решить уравнение  .
.
Решение. Характеристическое уравнение, соответствующее данному дифференциальному, имеет вид 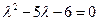 . Корни
. Корни  этого уравнения действительны и различны. Им отвечают два частных решения
этого уравнения действительны и различны. Им отвечают два частных решения 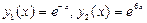 , с помощью которых записываем общее решение данного уравнения
, с помощью которых записываем общее решение данного уравнения  .
.
3.12). Решить уравнение  .
.
Решение. Характеристическое уравнение для данного дифференциального имеет вид: 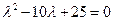 , или
, или  . Т.е. его корни
. Т.е. его корни  . В соответствии со случаем 2 Таблицы 2 частными решениями данного дифференциального уравнения, составляющими его фундаментальную систему решений, являются функции
. В соответствии со случаем 2 Таблицы 2 частными решениями данного дифференциального уравнения, составляющими его фундаментальную систему решений, являются функции  , а его общее решение имеет вид
, а его общее решение имеет вид  .
.
3.13). Решить уравнение  .
.
Решение. Характеристическое уравнение для данного дифференциального выглядит так:  . Оно имеет пару комплексно - сопряженных корней
. Оно имеет пару комплексно - сопряженных корней  . Здесь
. Здесь  . Соответствующие частные решения
. Соответствующие частные решения  составляют фундаментальную систему решений данного дифференциального уравнения, а его общее решение записывается так:
составляют фундаментальную систему решений данного дифференциального уравнения, а его общее решение записывается так:  .
.
Задания для самостоятельного решения
3.45.  . 3.46.
. 3.46. 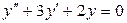 . 3.47.
. 3.47.  . 3.48.
. 3.48.  .
.
3.49.  . 3.50.
. 3.50. 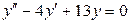 . 3.51.
. 3.51. 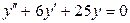 . 3.52.
. 3.52.  .
.
Ответы
3.45.  .3.46.
.3.46. 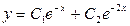 . 3.47.
. 3.47.  . 3.48.
. 3.48.  .
.
3.49.  . 3.50.
. 3.50.  .. 3.51.
.. 3.51. 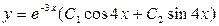 . 3.52.
. 3.52.  .
.
Линейные неоднородные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.
В том случае, когда в ЛНДУ второго порядка, т.е. в уравнении (22) при  , коэффициенты в левой его части являются постоянными, оно имеет вид
, коэффициенты в левой его части являются постоянными, оно имеет вид
 (3.30)
(3.30)
Следуя формуле (3.27), сначала (с помощью характеристического уравнения) необходимо решить соответствующее ему ЛОДУ:  . Второе слагаемое в формуле (3.27), некоторое частное решение
. Второе слагаемое в формуле (3.27), некоторое частное решение 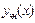 уравнения (3.30), может быть записано в виде функции того же типа, что и правая часть -
уравнения (3.30), может быть записано в виде функции того же типа, что и правая часть - 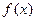 , если она имеет специальный вид, приведенный в следующей таблице.
, если она имеет специальный вид, приведенный в следующей таблице.
Таблица 3.
| № | 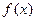 - правая часть ЛНДУ (30) - правая часть ЛНДУ (30)
| Корни характеристического уравнения (3.29) | Вид частного решения 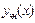
|
| I | 
| 1. Число 0 не является корнем характеристического уравнения | 
|
2. Число 0 -корень характеристического уравнения кратности 
| 
| ||
| II | 
| 1. Число  не является корнем характеристического уравнения не является корнем характеристического уравнения
| 
|
2.Число  -корень характеристического уравнения кратности -корень характеристического уравнения кратности 
| 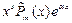
| ||
| III | 
| 1. Числа  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
|  , ,

|
2. Числа  являются корнями характеристического уравнения являются корнями характеристического уравнения
|  , ,

| ||
| IV | 
| 1. Числа  не являются корнями не являются корнями
|  , ,

|
2. Числа  являются корнями характеристического уравнения кратности являются корнями характеристического уравнения кратности 
| 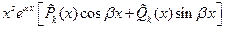 , ,

|
Указанные в этой таблице  ,
,  ,
,  ,
,  ,
,  - многочлены с неопределенными коэффициентами.
- многочлены с неопределенными коэффициентами.
3.14). Решить уравнение 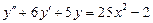 .
.
Решение. Однородное уравнение, соответствующее данному неоднородному имеет вид:
 . Его характеристическое уравнение
. Его характеристическое уравнение  имеет корни
имеет корни  , которым соответствуют частные решения
, которым соответствуют частные решения  ,
,  . По формуле (25)
. По формуле (25) 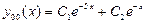 . Второе слагаемое в формуле (3.27), т.е. некоторое частное решение
. Второе слагаемое в формуле (3.27), т.е. некоторое частное решение 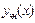 данного ЛНДУ, в соответствии с приведенной выше Таблицей 3, раздел I(1), является функцией подобной правой части
данного ЛНДУ, в соответствии с приведенной выше Таблицей 3, раздел I(1), является функцией подобной правой части  . А, так как среди корней характеристического уравнения нет числа
. А, так как среди корней характеристического уравнения нет числа 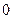 , то
, то
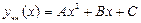 , (3.31)
, (3.31)
где  и
и  - неопределенные пока коэффициенты. Найдем эти числа, подставляя функцию (3.31) в исходное уравнение, которому она должна удовлетворять. Так как
- неопределенные пока коэффициенты. Найдем эти числа, подставляя функцию (3.31) в исходное уравнение, которому она должна удовлетворять. Так как 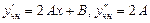 , то получим равенство
, то получим равенство  , или
, или






