Используя геометрический смысл определенного интеграла, вычисляется площадь фигуры, ограниченной графиками функций  ,
,  и прямыми
и прямыми  , по формуле
, по формуле
 .
.
1.29). Найти площадь, ограниченную параболой  и прямой
и прямой 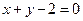 .
.
Решение. Решая систему данных уравнений, находим абсциссы двух точек пересечения прямой  и параболы
и параболы  :
:  . По приведенной выше формуле
. По приведенной выше формуле

 .
.
Интеграл с бесконечным промежутком интегрирования (несобственный интеграл)
Пусть функция 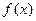 непрерывна на промежутке
непрерывна на промежутке  . Интеграл по бесконечному промежутку
. Интеграл по бесконечному промежутку  называется несобственным интегралом первого рода. Для вычисления этого интеграла используется формула
называется несобственным интегралом первого рода. Для вычисления этого интеграла используется формула 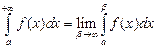 .
.
Интеграл  называется сходящимся, если в вышеуказанной формуле существует конечный предел
называется сходящимся, если в вышеуказанной формуле существует конечный предел  , в противном случае этот интеграл называется расходящимся.
, в противном случае этот интеграл называется расходящимся.
Аналогично,  и
и
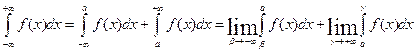 , где
, где  .
.
1.30). Исследовать на сходимость и, если интеграл сходится, вычислить 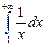 .
.
По определению несобственного интеграла первого рода
 . Таким образом, данный интеграл расходится.
. Таким образом, данный интеграл расходится.
1.31). Вычислить интеграл  или установить его расходимость.
или установить его расходимость.
По определению 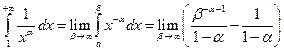 . В случае
. В случае 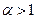 и при
и при 
 , т.е. существует конечный предел, значит, интеграл сходится и
, т.е. существует конечный предел, значит, интеграл сходится и
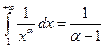 . В случае
. В случае  и при
и при  ,
,  . Таким образом, в этом случае интеграл расходится.
. Таким образом, в этом случае интеграл расходится.
Задания для самостоятельного решения
1.50 – 1.63. Вычислить интегралы.
1.64. – 1.70. Вычислить площадь плоской фигуры, ограниченной данными линиями.
1.71. – 1.77. Вычислить интегралы или установить их расходимость.
1.50.  . 1.57.
. 1.57.  . 1.64.
. 1.64.  . 1.71.
. 1.71. 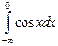 .
.
1.51.  . 1.58.
. 1.58. 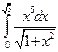 . 1.65.
. 1.65.  . 1.72.
. 1.72.  .
.
1.52.  . 1.59.
. 1.59. 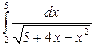 . 1.66.
. 1.66.  . 1.73.
. 1.73.  .
.
1.53.  . 1.60.
. 1.60.  . 1.67.
. 1.67.  . 1.74.
. 1.74.  .
.
1.54.  . 1.61.
. 1.61.  . 1.68.
. 1.68. 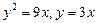 . 1.75.
. 1.75.  .
.
1.55.  . 1.62.
. 1.62.  . 1.69.
. 1.69. 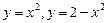 . 1.76.
. 1.76. 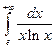 .
.
1.56.  . 1.63.
. 1.63. 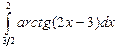 . 1.70.
. 1.70.  . 1.77.
. 1.77. 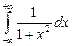 .
.
Ответы.
1.50.  . 1.57.
. 1.57.  . 1.64. 10,67. 1.71. Расходится.
. 1.64. 10,67. 1.71. Расходится.
1.51. 1. 1.58.  . 1.65.
. 1.65.  . 1.72. 1.
. 1.72. 1.
1.52.  . 1.59. 1,57. 1.66. 1,23. 1.73.
. 1.59. 1,57. 1.66. 1,23. 1.73.  .
.
1.53. 2,01. 1.60. 0,57. 1.67. 29,87. 1.74. Расходится.
1.54. 0, 33. 1.61. 1,57. 1.68. 0,50. 1.75.  .
.
1.55. 1, 50. 1.62. -0, 25. 1.69. 2, 67. 1.76. Расходится.
1.56. 0,50. 1.63. 0,21. 1.70. 0,75. 1.77.  .
.
Контрольная работа № 1. Интегрирование.
1.- 8. Вычислить неопределенные интегралы.
9. Вычислить определенный интеграл.
10. Вычислить площадь фигуры, ограниченной данными линиями.
Вариант 1.
1. 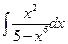 . 2.
. 2. 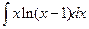 . 3.
. 3. 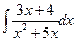 . 4.
. 4.  . 5.
. 5.  .
.
6.  . 7.
. 7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  .
.
Вариант 2.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4. 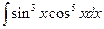 . 5.
. 5.  .
.
6.  . 7.
. 7.  . 8.
. 8. 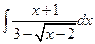 . 9.
. 9.  . 10.
. 10.  .
.
Вариант 3.
1.  .2.
.2.  . 3.
. 3. 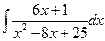 . 4.
. 4.  . 5.
. 5.  .
.
6.  . 7.
. 7.  . 8.
. 8. 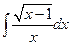 . 9.
. 9.  . 10.
. 10.  .
.
Вариант 4.
1. 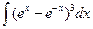 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  . 7.
. 7. 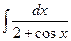 . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  .
.
Вариант 5.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  . 8.
. 8.  . 9.
. 9.  . 10.
. 10.  .
.
Вариант 6.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  . 7.
. 7.  . 8.
. 8.  . 9.
. 9. 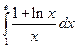 . 10.
. 10.  .
.
Вариант 7.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5. 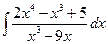 .
.
6.  .7.
.7.  .8.
.8.  . 9.
. 9. 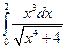 . 10.
. 10. 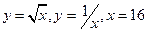 .
.
Вариант 8.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  .8.
.8.  . 9.
. 9.  . 10.
. 10.  .
.
Вариант 9.
1.  . 2.
. 2.  . 3.
. 3. 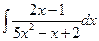 . 4.
. 4.  . 5.
. 5.  .
.
6. 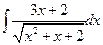 .7.
.7.  .8.
.8.  .9.
.9.  .10.
.10.  .
.
Вариант 10.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  .8.
.8.  .9.
.9. 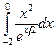 .10.
.10. 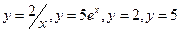 .
.
Вариант 11.
1. 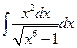 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  .8.
.8.  .9.
.9. 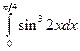 .10.
.10.  .
.
Вариант 12.
1. 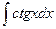 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  .8.
.8.  .9.
.9.  .10.
.10. 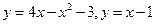 .
.
Вариант 13.
.  . 2.
. 2.  . 3.
. 3. 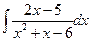 . 4.
. 4.  . 5.
. 5.  .
.
6. 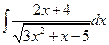 .7.
.7.  .8.
.8.  .9.
.9.  .10.
.10.  .
.
Вариант 14.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  .8.
.8.  .9.
.9.  .10
.10 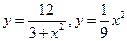 .
.
Вариант 15.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4. 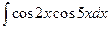 . 5.
. 5.
6.  .7.
.7.  .8.
.8. 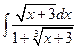 . 9.
. 9.  .10.
.10.  .
.
Вариант 16.
1.  . 2.
. 2.  . 3.
. 3. 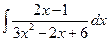 . 4.
. 4.  .5.
.5.  .
.
6. 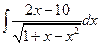 .7.
.7.  .8.
.8.  .9.
.9.  .10.
.10.  .
.
Вариант 17.
1.  . 2.
. 2.  . 3.
. 3. 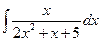 . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  .8.
.8.  .9.
.9.  .10.
.10. 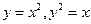 .
.
Вариант 18.
1. 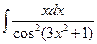 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  .8.
.8.  . 9.
. 9. 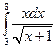 .10.
.10.  ,
,
Вариант 19.
1.  . 2.
. 2. 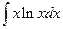 . 3.
. 3.  . 4.
. 4.  .5.
.5.  .
.
6.  .7.
.7.  .8.
.8.  . 9.
. 9.  .10.
.10.  .
.
Вариант 20.
1. 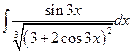 . 2.
. 2.  . 3.
. 3. 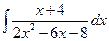 . 4.
. 4.  .5.
.5.  .
.
6.  .7.
.7. 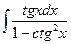 .8.
.8.  . 9.
. 9.  .10.
.10. 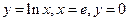 .
.
Вариант 21.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4. 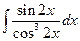 .5.
.5.  .
.
6. 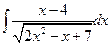 .7.
.7.  .8.
.8.  . 9.
. 9.  .10.
.10.  .
.
Вариант 22.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .5.
.5.  .
.
6.  .7.
.7. 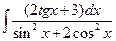 .8.
.8.  . 9.
. 9.  .10.
.10.  .
.
Вариант 23.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  .8.
.8.  . 9.
. 9.  .10.
.10.  .
.
Вариант 24.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  . 5.
. 5.  .
.
6.  .7.
.7.  .8.
.8. 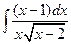 . 9.
. 9.  . 10.
. 10.  .
.
Вариант 25.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4. 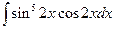 . 5.
. 5.  .
.
6. 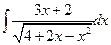 .7.
.7.  .8.
.8.  . 9.
. 9. 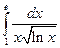 .10.
.10. 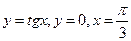 .
.
Вариант 26.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .5.
.5.  .
.
6. 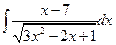 .7.
.7.  .8.
.8.  .9.
.9.  .10.
.10. 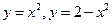 .
.
Вариант 27.
1.  . 2.
. 2.  . 3.
. 3. 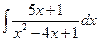 . 4.
. 4. 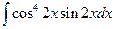 . 5.
. 5. 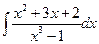 .
.
6.  .7.
.7.  .8.
.8.  .9.
.9.  .10.
.10.  .
.
Вариант 28.
1.  . 2.
. 2.  . 3.
. 3.  .4.
.4. 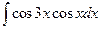 .5.
.5.  .
.
6. 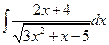 .7.
.7.  .8.
.8.  . 9.
. 9.  .10.
.10. 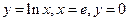 .
.
Вариант 29.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4. 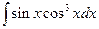 .5.
.5.  .
.
6.  .7.
.7.  .8.
.8.  . 9.
. 9. 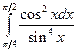 .10.
.10.  .
.
Вариант 30.
1.  . 2.
. 2.  . 3.
. 3.  .4.
.4. 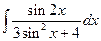 .5.
.5.  .
.
6.  .7.
.7.  .8.
.8.  .9.
.9.  .10.
.10. 
2. Функции нескольких переменных
2.1. Основные определения
Если каждой точке  из некоторого подмножества
из некоторого подмножества  пространства
пространства 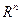 по некоторому правилу или закону поставлено в соответствие единственное значение переменной
по некоторому правилу или закону поставлено в соответствие единственное значение переменной  из множества
из множества  , то говорят, что задана функция нескольких переменных (
, то говорят, что задана функция нескольких переменных ( переменных):
переменных):  . Подмножество
. Подмножество  называется областью определения этой функции, а
называется областью определения этой функции, а  - множеством ее значений.
- множеством ее значений.
Например,  - функция двух переменных,
- функция двух переменных,  - функция трех переменных. В этом разделе будут рассмотрены некоторые из понятий дифференциального исчисления функций двух переменных:
- функция трех переменных. В этом разделе будут рассмотрены некоторые из понятий дифференциального исчисления функций двух переменных:  .
.
Графиком функции двух переменных  называется множество точек
называется множество точек 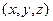 трехмерного пространства
трехмерного пространства 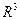 , таких, что
, таких, что  и
и  . Таким образом, график представляет собой поверхность - множество точек с координатами
. Таким образом, график представляет собой поверхность - множество точек с координатами  в пространстве
в пространстве 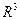 .
.
2.1). Найти область определения функции  . Существование этой функции обеспечивает условие
. Существование этой функции обеспечивает условие 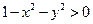 , т.е.
, т.е.  . Таким образом, областью определения
. Таким образом, областью определения  данной функции является внутренность круга с центром в начале координат и радиусом 1.
данной функции является внутренность круга с центром в начале координат и радиусом 1.
Для построения поверхности – графика функции  используется метод сечений этой поверхности плоскостями, параллельными координатной плоскости
используется метод сечений этой поверхности плоскостями, параллельными координатной плоскости  , т.е. системой плоскостей
, т.е. системой плоскостей  , где произвольное число
, где произвольное число  . Пересечение поверхности
. Пересечение поверхности  с плоскостью
с плоскостью  определяется равенством
определяется равенством  .
.
Линией уровня функции двух переменных  называется множество точек плоскости
называется множество точек плоскости  , удовлетворяющих равенству
, удовлетворяющих равенству  . Число
. Число  здесь называют уровнем. Итак, для точек, принадлежащих одной линии уровня, функция принимает одно и то же значение, равное
здесь называют уровнем. Итак, для точек, принадлежащих одной линии уровня, функция принимает одно и то же значение, равное  .
.
2.2). Найти линии уровня функции  . Построить ее график. Линии уровня данной функции определяются уравнениями
. Построить ее график. Линии уровня данной функции определяются уравнениями  , где
, где  . Эти уравнения описывают множество концентрических окружностей в плоскости
. Эти уравнения описывают множество концентрических окружностей в плоскости  с общим центром в начале координат с радиусами
с общим центром в начале координат с радиусами  . График этой функции представляет собой поверхность
. График этой функции представляет собой поверхность  , называемую параболоидом.
, называемую параболоидом.
Число  называется пределом функции
называется пределом функции  в точке
в точке  (
( ), если для любого сколь угодно малого положительного числа
), если для любого сколь угодно малого положительного числа  (
( ) найдется такое положительное число
) найдется такое положительное число  (
( ), что для всех точек
), что для всех точек  , отстоящих от точки
, отстоящих от точки  на расстояние меньшее, чем
на расстояние меньшее, чем  (такое множество точек называется
(такое множество точек называется  -окрестностью
-окрестностью  точки
точки  :
:  ), выполняется неравенство
), выполняется неравенство  . Если предел существует, то он не зависит от пути, по которому точка
. Если предел существует, то он не зависит от пути, по которому точка  стремится к точке
стремится к точке  .
.
2.3).  .
.
2.4).  . Например, при
. Например, при  , т.е., если точка
, т.е., если точка  стремится к точке
стремится к точке  по прямой
по прямой  , предел равен
, предел равен 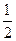 . Если же
. Если же  , т.е. точка
, т.е. точка  стремится к точке
стремится к точке  по прямой
по прямой  . В этом случае предел оказывается равен
. В этом случае предел оказывается равен  . Итак, предел в этом примере не существует, так как при стремлении точки
. Итак, предел в этом примере не существует, так как при стремлении точки  к точке
к точке  по различным путям, он получается различным.
по различным путям, он получается различным.
Функция 
 называется непрерывной в точке
называется непрерывной в точке  , если
, если
- функция
 определена в точке
определена в точке  и в некоторой ее окрестности,
и в некоторой ее окрестности, - существует конечный предел
 при стремлении точки
при стремлении точки  к точке
к точке  произвольным образом,
произвольным образом, -
 .
.
Функция разрывна в точке  , если нарушено хотя бы одно из условий 1., 2., 3.
, если нарушено хотя бы одно из условий 1., 2., 3.
Функция  непрерывная в любой точке некоторой области
непрерывная в любой точке некоторой области  называется непрерывной в этой области.
называется непрерывной в этой области.
2.5). Функция  определена во всех точках плоскости
определена во всех точках плоскости 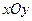 , но не в точке
, но не в точке 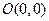 , поэтому разрывна в этой точке. В остальных точках плоскости она непрерывна.
, поэтому разрывна в этой точке. В остальных точках плоскости она непрерывна.
2.6). Функция  разрывна в точке
разрывна в точке 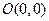 , так как не имеет предела в этой точке.
, так как не имеет предела в этой точке.
2.7). Функция  разрывна в точке
разрывна в точке  , поскольку
, поскольку 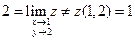 .
.
Теорема. Если функция  непрерывна в ограниченной замкнутой области
непрерывна в ограниченной замкнутой области  , то
, то
a) она в этой области ограничена, т.е. существует число  (
( ) такое, что для всех точек
) такое, что для всех точек 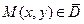 выполняется неравенство
выполняется неравенство  ,
,
b) в области  имеются точки, в которых функция достигает своего наименьшего и наибольшего значений.
имеются точки, в которых функция достигает своего наименьшего и наибольшего значений.
2.2.Частные производные функции двух переменных. Полный дифференциал.
Рассмотрим функцию  . Пусть
. Пусть  - область ее определения. Зафиксируем точку
- область ее определения. Зафиксируем точку  . Придадим аргументам
. Придадим аргументам  и
и  приращения
приращения  и
и  соответственно. При этом
соответственно. При этом 
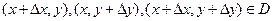 . Тогда разности
. Тогда разности  и
и
 называются частными приращениями функции
называются частными приращениями функции  по переменным
по переменным  и
и  соответственно, а разность
соответственно, а разность  - ее полным приращением.
- ее полным приращением.
Частными производными функции  по переменным
по переменным  и
и  называются следующие пределы разностных отношений
называются следующие пределы разностных отношений 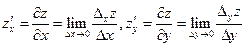 .
.
Значение частной производной функции зависит от точки  , в которой она вычисляется, т.е. сама по себе частная производная является функцией точки
, в которой она вычисляется, т.е. сама по себе частная производная является функцией точки  . Формулы и правила, используемые при вычислении производной функции одной переменной, справедливы также и для частных производных функции двух переменных. Главное в процессе вычисления частной производной функции по одной из ее переменных – помнить, что другая переменная при этом считается постоянной.
. Формулы и правила, используемые при вычислении производной функции одной переменной, справедливы также и для частных производных функции двух переменных. Главное в процессе вычисления частной производной функции по одной из ее переменных – помнить, что другая переменная при этом считается постоянной.
2.8). Вычислить частные производные функции  .
.
 ,
,  .
.
Частные производные, как функции тех же переменных, тоже в свою очередь могут иметь частные производные, которые называются частными производными второго порядка.
 ,
,  ,
,  ,
,  ,
,
Смешанные производные  и
и  равны между собой, если они являются непрерывными функциями.
равны между собой, если они являются непрерывными функциями.
2.9). Вычислить частные производные второго порядка функции  .
.
Пользуясь уже имеющимися в примере 36) частными производными первого порядка, получаем  ,
,  ,
,  ,
,
 . Как видим,
. Как видим,  .
.
Если функция  имеет в точке
имеет в точке  непрерывные частные производные, то ее полное приращение может быт представлено в виде
непрерывные частные производные, то ее полное приращение может быт представлено в виде  , где
, где
 и
и  при
при  . Главная линейная часть
. Главная линейная часть 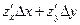 полного приращения
полного приращения  функции
функции  называется ее полным дифференциалом
называется ее полным дифференциалом  , с учетом того, что для независимых переменных
, с учетом того, что для независимых переменных  и
и  .
.
2.10). Полный дифференциал функции  записываем, следуя формуле
записываем, следуя формуле


2.3.Производная по направлению. Градиент.
Пусть функция  определена в некоторой области
определена в некоторой области  . Точка
. Точка  ,
, 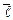 - некоторое направление (вектор с началом в точке М), задаваемое единичным вектором (ортом)
- некоторое направление (вектор с началом в точке М), задаваемое единичным вектором (ортом)
 , где
, где  и
и  - косинусы углов, образуемых вектором
- косинусы углов, образуемых вектором 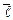 с осями координат, называемые направляющими косинусами. При перемещении из точки
с осями координат, называемые направляющими косинусами. При перемещении из точки  в точку
в точку  по направлению
по направлению 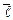 функция получает приращение
функция получает приращение
 , называемое приращением функции в данном направлении
, называемое приращением функции в данном направлении 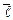 . Пусть
. Пусть  - величина перемещения. Предел отношения
- величина перемещения. Предел отношения  при
при 
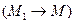 , если он существует, называется производной функции
, если он существует, называется производной функции  по направлению
по направлению 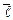 и обозначается
и обозначается  , или
, или  . Итак,
. Итак,  . Производная
. Производная  характеризует изменения функции в направлении
характеризует изменения функции в направлении 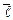 . При заданных направляющих косинусах производная по направлению вычисляется по формуле
. При заданных направляющих косинусах производная по направлению вычисляется по формуле  .
.
Градиентом функции  в точке
в точке  называется вектор
называется вектор  , координаты которого равны соответствующим частным производным
, координаты которого равны соответствующим частным производным  и
и 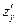 , вычисленным в точке
, вычисленным в точке  . Т.е.
. Т.е.  , или
, или  . Градиент, это вектор, указывающий направление наибольшего роста функции.
. Градиент, это вектор, указывающий направление наибольшего роста функции.
2.11). Вычислить производную функции  в точке
в точке  по направлению
по направлению  .
.
Найдем длину вектора 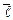 :
:  . Тогда
. Тогда  . Таким образом, единичный орт
. Таким образом, единичный орт  вектора
вектора 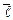 имеет координаты
имеет координаты  . Используя частные производные
. Используя частные производные  и
и 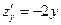 , запишем производную по направлению
, запишем производную по направлению 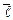 в произвольной точке
в произвольной точке  :
: 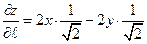
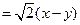 . Итак, в точке
. Итак, в точке  эта производная оказывается равной
эта производная оказывается равной  .
.
2.12). Вычислить градиент функции  в точке
в точке  .
.
Градиент этой функции в произвольной точке  выглядит так
выглядит так  . В данной точке
. В данной точке 
 .
.
2.4.Экстремум функции двух переменных.






