Интегралы вида  рационализируются универсальной тригонометрической подстановкой:
рационализируются универсальной тригонометрической подстановкой:  . При этомиспользуются формулы, выражающие синус и косинус через тангенс половинного аргумента
. При этомиспользуются формулы, выражающие синус и косинус через тангенс половинного аргумента
 .
.
Кроме того, при замене переменной в этом интеграле учитываем, что 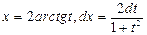 .
.
Рационализация с помощью универсальной подстановки иногда приводит к громоздким подынтегральным функциям. В некоторых частных случаях эффективнее использовать подстановки  или
или  .
.
1.19). 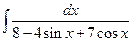



 . В этом примере использована универсальная подстановка.
. В этом примере использована универсальная подстановка.
1.20). 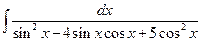
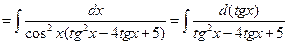 . Здесь удобно выполнить замену
. Здесь удобно выполнить замену  . И, так как
. И, так как 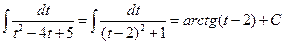 , то
, то
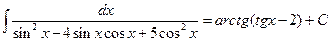 .
.
В интегралах вида  , если
, если  и
и  - четные положительные числа, используются формулы понижения степени:
- четные положительные числа, используются формулы понижения степени:  . Если же
. Если же  или
или  - нечетное число, интеграл находят, отделяя от нечетной степени один множитель.
- нечетное число, интеграл находят, отделяя от нечетной степени один множитель.
1.21).  =
= 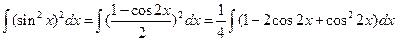


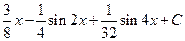 . Здесь
. Здесь 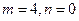 .
.
1.22). 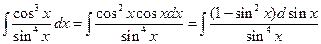 . Обозначив
. Обозначив  , получим
, получим

 . Здесь
. Здесь  .
.
Интегралы вида  находятся с помощью тригонометрических формул:
находятся с помощью тригонометрических формул:  ,
,
 ,
,  .
.
1.23). 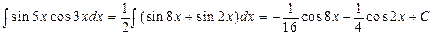 .
.
Задания для самостоятельного решения
1.29.  . 1.36.
. 1.36.  . 1.43.
. 1.43.  .
.
1.30.  . 1.37.
. 1.37.  . 1.44.
. 1.44.  .
.
1.31.  . 1.38.
. 1.38.  . 1.45.
. 1.45.  .
.
1.32.  . 1.39.
. 1.39.  . 1.46.
. 1.46.  .
.
1.33.  . 1.40.
. 1.40. 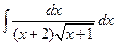 . 1.47.
. 1.47. 
1.34.  1.41.
1.41.  . 1.48.
. 1.48.  .
.
1.35.  . 1.42.
. 1.42.  . 1.49.
. 1.49.  .
.
Ответы.
1.29.  1.36.
1.36.  . 1.43.
. 1.43.  .
.
 .
.
1.30.  . 1.37.
. 1.37.  . 1.44.
. 1.44.  .
.
1.31.  . 1.38.
. 1.38.  . 1.45.
. 1.45.  .
.
1.32.  .1.39.
.1.39. 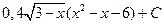 1.46.
1.46. 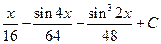 .
.
1.33.  . 1.40.
. 1.40. 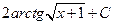 . 1.47.
. 1.47. 
1.34.  . 1.41.
. 1.41. 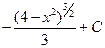
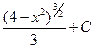 . 1.48.
. 1.48.  .
.
1.35.  . 1.42.
. 1.42.  . 1.49.
. 1.49.  .
.
1.2.Определенный интеграл.
Функция 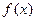 определена и ограничена на отрезке
определена и ограничена на отрезке  . Произвольно выбранными точками
. Произвольно выбранными точками
 разобьем этот отрезок на
разобьем этот отрезок на  элементарных отрезков
элементарных отрезков  ,
, 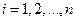 , длина каждого из которых равна
, длина каждого из которых равна  . В каждом из этих элементарных отрезков произвольно выберем точку
. В каждом из этих элементарных отрезков произвольно выберем точку  ,
,  . Сумма вида
. Сумма вида

называется  -ой интегральной суммой функции
-ой интегральной суммой функции  на отрезке
на отрезке  . Если
. Если 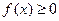 на
на  , то
, то  - площадь ступенчатой фигуры. Обозначим
- площадь ступенчатой фигуры. Обозначим 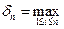
 .
.
Конечный предел последовательности интегральных сумм при  и
и  называется определенным интегралом от функции
называется определенным интегралом от функции 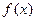 на отрезке
на отрезке  и обозначается
и обозначается
 .
.
Предел в этом определении не зависит от способа разбиения отрезка  на элементарные отрезки и выбора в каждом из них промежуточных точек
на элементарные отрезки и выбора в каждом из них промежуточных точек  . Здесь
. Здесь  - переменная интегрирования,
- переменная интегрирования, 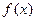 - подынтегральная функция,
- подынтегральная функция,  - подынтегральное выражение,
- подынтегральное выражение,  - отрезок интегрирования,
- отрезок интегрирования,  и
и  - нижний и верхний пределы интегрирования. Если определенный интеграл существует, то функцию
- нижний и верхний пределы интегрирования. Если определенный интеграл существует, то функцию 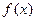 называют интегрируемой на отрезке
называют интегрируемой на отрезке  . В частности, непрерывность подынтегральной функции на отрезке
. В частности, непрерывность подынтегральной функции на отрезке  обеспечивает ее интегрируемость на этом отрезке.
обеспечивает ее интегрируемость на этом отрезке.
Геометрический смысл определенного интеграла.
Если 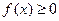 на
на  , то
, то 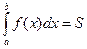 - это площадь криволинейной трапеции – плоской фигуры, ограниченной графиком функции
- это площадь криволинейной трапеции – плоской фигуры, ограниченной графиком функции  , осью
, осью  и двумя прямыми
и двумя прямыми  .
.
Теорема. Если функция определена и непрерывна на  всюду, за исключением конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.
всюду, за исключением конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.
Свойства определенного интеграла.
1.  (
( ). 2.
). 2.  .
.
3.  . 4.
. 4.  .
.
5.  6. Если,
6. Если,  , то
, то  .
.
7. Если  , то
, то  . 8.
. 8.  .
.
9. Если  , где
, где 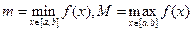 , то
, то
 .
.
10. Если 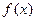 непрерывна на
непрерывна на  , то существует точка
, то существует точка  , такая, что
, такая, что
 .
.




