Целью работы является:
1. изучение влияния интервала дискретизации Т на устойчивость цифровых автоматических систем регулирования (ЦАСР);
2. изучение влияния интервала дискретизации Т на параметры переходного процесса в цифровых автоматических системах регулирования;
3. Экспериментальное исследование влияния интервала дискретизации Т на устойчивость и параметры переходного процесса ЦАСР.
Домашняя подготовка и составление предварительного отчета
1. Изучить рекомендуемую литературу [1; 2, с.21–28].
2. Для заданной схемы АСР (табл.4, рис.4), изменить параметры первого звена: для схем рис.4, а,б коэффициент k 1 уменьшить в два раза по сравнению с табличным, для схемы рис.4, в постоянную времени Т 1 уменьшить в два раза:
а) проверить условие устойчивости по критерию Гурвица. Убедиться, что аналоговая АСР устойчива;
б) оценить время регулирования АСР, перерегулирование и колебательность переходного процесса для возмущающего воздействия Х вв;
в) Включить в схему АСР аналого-цифровой (АЦП) и цифро-аналоговый (ЦАП) преобразователи и определить интервал дискретизации Т кр, при котором нарушается устойчивость ЦАСР.

Рис.6.1. Исследуемая схема аналоговой АСР

Рис.6.2. Исследуемая схема ЦАСР
Указания. К п.2. Параметры переходного процесса анализируются только по входу Х вв. для определения параметров использовать частотный критерий.
Для упрощения анализа АСР в дальнейших исследованиях целесообразно считать значение Х пред=0.
Для получения полной схемы ЦАСР преобразовать аналоговую схему рис.6.1 к виду, представленному на рис.6.2
Передаточная функция цифрового регулятора W 1(z) определяется при подстановке в функцию W 1(p) простейшую замену p =(z- 1) /T, где Т -интервал дискретизации. В линеаризованной ЦАСР произведение k АЦП· k ЦАП =1, а передаточная функция ЦАП определяется выражением W ЦАП(z, p)=  .
.
Следовательно, передаточная функция разомкнутой ЦАСР W раз(z, p) является функцией двух аргументов. Аналоговая часть, зависящая от аргумента р, функции W раз(z, p) совместно с передаточными функциями второго и третьего звеньев W 2(p) и W 3(p) должны быть преобразованы в функцию аргумента z. Для этого в этих функциях производится замена p =(z- 1) /T. Для определения интервала дискретизации Т кр, при котором нарушается устойчивость ЦАСР, записывается характеристическое уравнение замкнутой ЦАСР и используется критерий Гурвица.
Работа в лаборатории
Провести анализ влияния интервала дискретизации на параметры регулирования ЦАСР по заданной программе:
а) для заданной аналоговой АСР провести проверку устойчивости и определить параметры переходного процесса и запас устойчивости;
б) включить в схему аналого–цифровой и цифроаналоговый преобразователи, определить значение интервала дискретизации Ткр, при котором нарушается устойчивость. Для нескольких значений интервала дискретизации, меньших Т кр, определить параметры переходного процесса и запас устойчивости.
Сравнить результаты п. а) и б) и сделать выводы.
Указания. Собрать схему заданной аналоговой АСР (рис.6.1). Для упрощения схемы в дальнейших исследованиях целесообразно считать значение Х пред =0. В качестве Х вв использовать источник единичного скачка (ИЕС), он подключается на вход исследуемой АСР, один вход осциллографа – к выходу ИЕС, а второй – на выход АСР.
а) При подаче на АСР прямоугольного импульса Х вв проверяется устойчивость АСР и оцениваются по осциллограмме параметры переходного процесса (время регулирования, перерегулирование и колебательность, если процесс колебательный).
Разомкнуть АСР. Для снятия частотных характеристик источник единичного скачка заменить источником синусоидального сигнала (ИСС). Затем по осциллограммам определить отношение амплитуд (АЧХ) и разность фаз (ФЧХ) выходного и входного сигналов при изменении частоты входного синусоидального сигнала от 0 до 5·2π/ Тi, где Тi – минимальная постоянная времени звена исследуемой АСР. По снятым частотным характеристикам построить на комплексной плоскости АФХ разомкнутой АСР и сделать вывод о поведении АФХ в окрестности точки (–1, j 0). Определить графически запас устойчивости по модулю и по фазе.
б) Собрать схему заданной цифровой АСР (рис.6.2). Для упрощения исследования в дальнейших исследованиях целесообразно считать значение Х пред = 0. В качестве Х вв использовать источник единичного скачка (ИЕС), один вход осциллографа – к выходу ИЕС, а второй – на выход ЦАСР. Увеличивая интервал дискретизации от 0,001 с, определить значение Т кр, при котором нарушается устойчивость.
Замечание: значения интервала дискретизации менять в векторах коэффициентов знаменателя и числителя, а также в параметрах вычисления Sample time цифровых элементов.
Для значений интервала дискретизации, равных 0,25 Т кр, 0,5 Т кр, 0,9 Т кр, определить по осциллограмме параметры переходного процесса.
В блок задания функции MATLAB Fcn записать функцию W раз(z, p), в которой p = j ω, z=exp(jωT) и установить режим вычисления Complex. На вход блока подключается источник линейно изменяющегося воздействия Ramp, на выход – блок вычисления модуля и аргумента комплексного числа Complex to Magnitude-Angle, вычисленные модуль и аргумент комплексного числа подаются на осциллограф. Зарисовать осциллограммы модуля (АЧХ) и аргумента (ФЧХ) для значений интервала дискретизации, равных 0,25 Т кр, 0,5 Т кр, Т кр, 2 Т кр. Сигнал источника линейно изменяющегося воздействия Ramp представляет изменение частоты, максимальное значение которой задается выбирается большим из двух значений (5·2π/ Тi, 2·2π/ Т), где Тi – минимальная постоянная времени звена исследуемой АСР, где Т – интервал дискретизации.
По частотным характеристикам построить на комплексной плоскости АФХ разомкнутой ЦАСР и сделать вывод о поведении АФХ в окрестности точки (–1, j 0). Определить графически запас устойчивости по модулю и по фазе.
Построить зависимость параметров переходного процесса и запас устойчивости от интервала дискретизации. Учесть, что характеристики аналоговой АСР есть частный случай характеристик ЦАСР при нулевом интервале дискретизации.
Литература
1. Алексеев О.П., Казанский В.Е., Козис B.Л. и др. Автоматика электроэнергетических систем. Под. ред. В.Л. Козиса, Н.И. Овчаренко. – М.: Энергоиздат, 1981. – 480 с.
2. Гетта Т.Г. Автоматические системы регулирования с цифровыми регуляторами. –М.: Моск. энерг. ин–т, 1988, 52 с.
Контрольные вопросы
1. Каким уравнением описывается:
· безынерционное звено?
· апериодическое звено?
· интегрирующее звено?
· идеальное дифференцирующее звено?
· реальное дифференцирующее звено?
2. Дать определение передаточной функции.
3. Записать передаточную функцию:
· безынерционного звена?
· апериодического звена?
· интегрирующего звена?
· идеального дифференцирующего звена?
· реального дифференцирующего звена?
4. Дать определение амплитудно-частотной характеристики (АЧХ).
5. Указать на рис.7.1, какая АЧХ принадлежит:
· безынерционному звену?
· апериодическому звену?
· интегрирующему звену?
· идеальному дифференцирующему звену?
· реальному дифференцирующему звену?
Определить параметры выбранных звеньев.

Рис.7.1. Определение амплитудно-частотной характеристики
6. Дать определение фазо-частотной характеристики (ФЧХ).
7. Указать на рис.7.2, какая ФЧХ принадлежит:
· безынерционному звену?
· апериодическому звену?
· интегрирующему звену?
· идеальному дифференцирующему звену?
· реальному дифференцирующему звену?
Определить параметры выбранных звеньев.
8. Дать определение амплитудно-фазовой характеристики (АФХ).

Рис.7.2. Определение фазо-частотной характеристики
9. Указать на рис.7.3, какая АФХ принадлежит:
· безынерционному звену?
· апериодическому звену?
· интегрирующему звену?
· идеальному дифференцирующему звену?
· реальному дифференцирующему звену?
Определить параметры выбранных звеньев.
10. Дать определение переходной характеристики.
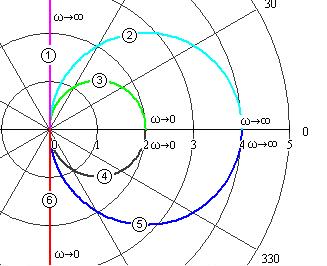
Рис.7.3. Определение амплитудно-фазовой характеристики
Рис.7.4. Определение переходной характеристики
11.Указать на рис.7.4, какая переходная характеристика принадлежит:
· безынерционному звену?
· апериодическому звену?
· интегрирующему звену?
· идеальному дифференцирующему звену?
· реальному дифференцирующему звену?
Определить параметры выбранных звеньев.
12. Определить сигнал на выходе
· безынерционного звена
· апериодического звена
· интегрирующего звена
· идеального дифференцирующего звена
· реального дифференцирующего звена
при подаче на вход сигнала 1 (рис.7.5)

Рис.7.5. Прохождение сигналов через звенья
Заключение
Методическое пособие содержит описание шести лабораторных работ, выполняемых на персональных компьютерах с использованием программы Simulink (пакет MATLAB). Пособие предназначено для студентов, обучающихся по направлению «Электроэнергетика», для закрепления знаний по таким теоретическим вопросам, как:
- типовые звенья автоматических систем регулирования;
· соединение типовых звеньев автоматических систем регулирования;
· исследование статических характеристик автоматических систем регулирования;
· анализ устойчивости автоматических систем регулирования;
- коррекция неустойчивых автоматических систем регулирования;
· анализ влияния интервала дискретизации на параметры регулирования цифровых автоматических систем регулирования.
Темы лабораторных работ поддерживают основную часть теоретического курса.




