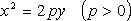его корни 
Классификация линий второй степени по числу центров
I группа - имеющие единственный центр симметрии,
II группа - не имеющие центра симметрии,
III группа - имеющие прямую центров симметрии.
Канонический вид линий второй степени
I группа: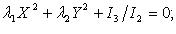 
II группа: 
III группа: 
где
Необходимые и достаточные признаки линий второй степени
Расположение эллипса и гиперболы относительно исходной системы координат
Координаты нового начала (центра) - решение системы
Угловой коэффициент новой оси 
(в случае 
)
Расположение параболы относительно исходной системы координат
Координаты вершины - решение системы, определяемой уравнением параболы и уравнением ее оси:
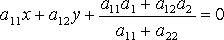
или
Параметр параболы: 
Направляющий вектор оси (в сторону ее вогнутости):
Поверхности второй степени
Канонические уравнения
Сфера
Сфера радиуса R с центром в начале координат:
Параметрические уравнения:
Сфера радиуса R с центром в точке S (a; b; c):
Эллипсоид (рис. 4.18)
Каноническое уравнение:
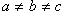- трехосный эллипсоид;
- эллипсоид вращения вокруг оси Oz;
- эллипсоид вращения вокруг оси Oy;
- эллипсоид вращения вокруг оси Ox;
- сфера.
Сечения эллипсоида плоскостями - либо эллипс (окружность), либо точка, либо 
.
Конус второй степени (рис. 4.19)
Каноническое уравнение:
a = b - конус вращения (прямой круговой).
Сечения конуса плоскостями: в плоскости, пересекающей все прямолинейные образующие, - эллипс; в плоскости, параллельной одной прямолинейной образующей, - парабола; в плоскости, параллельной двум прямолинейным образующим, - гипербола; в плоскости, проходящей через вершину конуса, - пара пересекающихся прямых или точка (вершина).
Однополостный гиперболоид (рис. 4.20)
Каноническое уравнение:
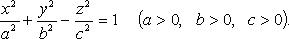
a = b - однополостный гиперболоид вращения вокруг оси Oz.
Горловой эллипс: 
Асимптотический конус: 
Сечения однополостного гиперболоида плоскостями - либо эллипс, либо парабола, либо гипербола, либо пара прямых (прямолинейных образующих).
Прямолинейные образующие
Через произвольную точку 
проходят две прямолинейные образующие с направляющими векторами 
и 
где:
В частности, если точку 
выбирать на горловом эллипсе 
то уравнениями прямолинейных образующих будут:
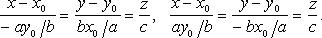
Двуполостный гиперболоид (рис. 4.21)
Каноническое уравнение:
a = b - двуполостный гиперболоид вращения вокруг оси Oz.
Асимптотический конус:
Сечения двуполостного гиперболоида плоскостями: либо эллипс, либо гипербола, либо парабола, либо точка, либо .
Эллиптический параболоид (рис. 4.22)
Каноническое уравнение:
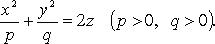
p = q - параболоид вращения вокруг оси Oz.
Сечения эллиптического параболоида плоскостями - либо эллипс, либо парабола, либо точка, либо .
Гиперболический параболоид (рис. 4.23)
Каноническое уравнение:
Сечения гиперболического параболоида плоскостями - либо гипербола, либо парабола, либо пара прямых (прямолинейных образующих).
Прямолинейные образующие
Через каждую точку проходят две прямолинейные образующие:
Эллиптический цилиндр (рис. 4.24)
Каноническое уравнение:
при a = b - круговой цилиндр.
Гиперболический цилиндр (рис. 4.25)
Каноническое уравнение:
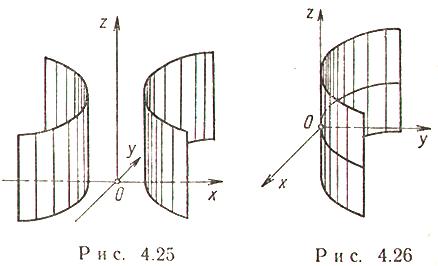
Параболический цилиндр (рис. 4.26)
Каноническое уравнение:
