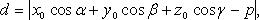Взаимное расположение двух прямых. Если прямые заданы уравнениями и то они:

Если прямые заданы уравнениями и то они:

1) параллельны (но не совпадают)

2) совпадают

3) пересекаются

4) скрещиваются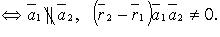

Если 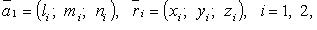то случаи 1 - 4 имеют место, когда ( 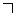- знак отрицания условия):

1)

2)

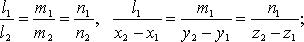
3)

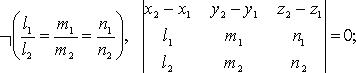
4)

Расстояние между двумя параллельными прямыми

В координатах

Расстояние между двумя скрещивающимися прямыми

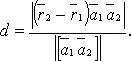
В координатах

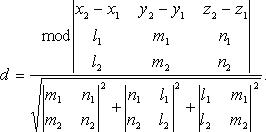
Угол между двумя прямыми

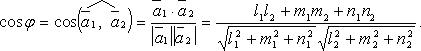
Необходимое и достаточное условие перпендикулярности двух прямых

или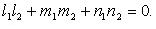

Взаимное расположение прямой и плоскости

Плоскость и прямая

1) пересекаются

2) прямая лежит в плоскости

3) параллельны

Если то случаи 1 - 3 имеют место, когда:

1)

2)

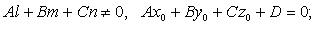
3)

Необходимое и достаточное условие параллельности прямой и плоскости

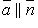или

Угол между прямой и плоскостью

Точка пересечения прямой с плоскостью

В координатах:

где

Уравнения прямой, проходящей через точку перпендикулярно к плоскости

В координатах:

Плоскость

Способы задания плоскости

Общее уравнение плоскости (рис. 4.13)

где - нормальный вектор плоскости.

В векторном виде .

Частные случаи общего уравнения плоскости:

1) By + Cz + D = 0 - параллельна оси Ox;

2) Ax + Cz + D = 0 - параллельна оси Oy;

3) Ax + By + D = 0 - параллельна оси Oz;

4) Cz + D = 0 - параллельна оси Oxy;

5) By + D = 0 - параллельна оси Oxz;

6) Ax + D = 0 - параллельна оси Oyz;

7) Ax + By + Cz = 0 - проходит через начало координат;

8) By + Cz = 0 - проходит через ось Ox;

9) Ax + Cz = 0 - проходит через ось Oy;

10) Ax + By = 0 - проходит через ось Oz;

11) z = 0 - плоскость Oxy;

12) y = 0 - плоскость Oxz;

13) x = 0 - плоскость Oyz.

Уравнение плоскости в отрезках

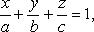
где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.

Нормальное уравнение плоскости

где - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.

Приведение общего уравнения плоскости к нормальному виду:

Здесь - нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если 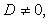произвольно, если D = 0.

Уравнение плоскости по точке и нормальному вектору

В векторном виде

В координатах

Уравнение плоскости по точке и двум неколлинеарным векторам

В векторном виде

В координатах

Уравнение плоскости по трем точкам

В векторном виде

В координатах

или

Параметрические уравнения плоскости

В векторном виде

В координатах

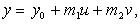
Уравнение плоскости, проходящей через две параллельные прямые и

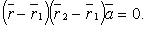
Если прямые заданы соответственно уравнениями:

и

то уравнение плоскости есть

Уравнение плоскости, проходящей через две пересекающиеся прямые и

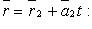
или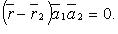

Если , то уравнение плоскости есть

Отклонение точки от плоскости

или

где знак перед корнем противоположен знаку D, если 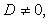и выбран произвольно, если D = 0.

Расстояние от точки до плоскости