В общей теории алгоритмов изучаются лишь принципиальная возможность алгоритмического решения задачи. При рассмотрении конкретных задач не обращается внимания на ресурсы времени и памяти для соответствующих им разрешающих алгоритмов. Однако нетрудно понять, что принципиальная возможность алгоритмического решения задачи еще не означает, что оно может быть практически получено. Поэтому возникает потребность уточнить понятие алгоритмической разрешимости, введя характеристики сложности алгоритмов, позволяющие судить об их практической реализуемости.
В качестве модели вычислительного устройства выберем МТ. Пусть МТ вычисляет функцию f(x). Определим функцию tT(x), равную числу шагов машины Т, выполненному при вычислении f(x), если f(x) определено. Если f(x) не определено, то значение tT(x) считается неопределенным. Функция tT(x) называется временной сложностью.
Активной зоной при работе машины Т на слове х называется множество всех ячеек ленты, которые либо содержат непустые символы, либо посещались в процессе вычисления f(x) устройством машины Т. Определим функцию sT(x), равную длине активной зоны при работе машины Т на слове х, если f(x) определено. Если f(x) не определено, то значение ST(x) считается неопределенным. Функция ST(x) называется емкостной (ленточной) сложностью.
Введенные функции ST(x) и tT(x) являются словарными.
Удобно ввести для рассмотрения функции натурального аргумента
Они также называются функциями временной и емкостной
сложности (по худшему случаю).
Классы сложности задач
Р задачи
Пусть П – некоторая массовая задача, характеризуемая множеством параметров, IÎП – индивидуальная задача, в которой эти параметры фиксированы. Пусть с массовой задачей П связана и зафиксирована схема кодирования α, которая ставит каждой индивидуальной
задаче IÎП в соответствие слово α(I) в некотором алфавите А. При этом под размером задачи I понимается длина слова α(I). Пусть Т –машина Тьюринга, решающая задачу П и
- соответствующая функция временной сложности (по худшему случаю).
О-символика: говорят, что неотрицательная функция f(n) не превосходит по порядку функцию g(n) и пишут f(n)=O(g(n)), если существует такая константа С, что f(n)≤C*g(n) для любого nÎN.
Говорят, что машина Т решает задачу П за полиномиальное время, если 
для некоторого полинома р. В противном случае говорят, что МТ Т решает задачу П за экспоненциальное время. К экспоненциальным оценкам относят, например, оценки вида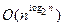 
, т. е. это оценки, которые превосходят любой полином, но меньше, чем 
для любого е>0.
Про задачу П говорят, что она разрешима за полиномиальное время, если существует машина Тьюринга Т, решающая ее за полиномиальное время. Обозначим через Р класс задач, разрешимых за полиномиальное время.
Имеется существенное различие между алгоритмами полиномиальной и экспоненциальной сложности. Ясно, что любой полиномиальный алгоритм более эффективен, кроме того, такие алгоритмы лучше реагируют на рост производительности компьютеров.
Рассмотрим такой параметр как размер решаемой задачи на ЭВМ за единицу времени с помощью данного алгоритма. Тогда изменение данного параметра при переходе к ЭВМ в 100 раз и в 1000 раз большей производительности для различных функций временной сложности показан в таблице:
| Функция временной сложности | Размер решаемой задачи за сутки | То же на ЭВМ в 100 раз быстрых | То же на ЭВМ в 1000 раз быстрых |
| n | N1 | 100 N1 | 1000 N1 |
| n2 | N2 | 10 N2 | 31,6 N2 |
| n3 | N3 | 4,64 N3 | 10 N3 |
| 2n | N4 | 6,64+N4 | 9,97+N4 |
| 3n | N5 | 4,19+N5 | 6,29+N5 |
Из таблицы видно, что в случае полиномиальных алгоритмов размер решаемой задачи при увеличении производительности ЭВМ увеличивается на мультипликативную константу, тогда как для экспоненциальных алгоритмов имеет место увеличение на аддитивную константу.
Полиномиальные алгоритмы обладают свойством “замкнутости”, их можно комбинировать полиномиальные, используя один в качестве “подпрограммы” другого и при этом результирующий алгоритм будет полиномиальным. В силу приведенных причин используется следующая терминология: полиномиальные алгоритмы называют эффективными, полиномиально решаемые задачи называют легкорешаемыми, а экспоненциально решаемые задачи называют труднорешаемыми.
Для практики важным является классификация задач по признаку труднорешаемости, хотя следует заметить, что установление легкорешаемости задачи еще не означает ее практическую решаемость. Например, установление полиномиальной оценки O(n1000) не гарантирует практической решаемости уже при начальных значениях n. Аналогичное замечание можно сделать относительно труднорешаемости. Заметим, что труднорешаемость задачи может быть связана с тем, что ее решение настолько велико, что не может быть записано в виде выражения, длина которого была бы ограничена полиномом от длины входа. Чтобы исключить этот тип труднорешаемости, рассматривается только такие задачи, которые имеют «короткий»
ответ.
Рассмотрим несколько примеров.
Пусть М ={1,2,…, n} – конечное множество, 
бинарное отношение на М. Рассмотрим задачу проверки – является ли R отношением эквивалентности (рефлексивное, симметричное, транзитивное). Будем задавать индивидуальную
задачу матрицей
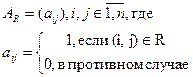
Ясно, что R будет отношением эквивалентности тогда и только тогда, когда матрица AR имеет единичную диагональ, симметрична и выполнено соотношение
где 
- матрица отношения R 2.
Кроме того, выполнено 
, где имеется в виду булево умножение матриц. Ясно, что сложность рассматриваемой задачи О(n2).
2. Бинарное отношение R называется связным, если для любых 
выполняется iRj или jRi.
Бинарное отношение называется Эйлеровым, если элементы R
R:(i1,j1);(i2,j2);…(it,jt),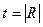 
можно упорядочить так, что выполнено
.
Можно доказать, что связное отношение R является эйлеровым тогда и только тогда, когда число единиц в матрице AR совпадает в i-ом столбце и в i-ой строке для каждого 
. Это дает алгоритм сложности O(n2), проверяющий эйлеровость отношения R.
3. Бинарное отношение R называется гамильтоновым, если элементы М i1,i2,…,in можно упорядочить так, что выполняется соотношение
(*)
В настоящее время неизвестно полиномиального алгоритма, который проверял бы гамильтоновость отношения R.
Тривиальный алгоритм требует n! упорядочений множества М и проверки условий (*), что, конечно, превосходит по величине любой полином от n.
4. Пусть f(x1,…,xn) – формула от булевых переменных x1,…,xn в некотором фиксированном базисе В. Формула f(x1,…,xn) называется выполнимой, если существует набор значений переменных x1,..., xn, такой, что f(x1,…,xn)=1.
Формула f(x1,…,xn) называется мультиафинной, если она имеет вид
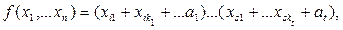
где a1,…,at – константы.
То есть f представляет собой конъюнкцию линейных форм.
Рассмотрим задачу проверки выполнимости мультиафинной формулы. Ясно, что существование выполняющего набора для мультиафинной формулы сводится к существованию решения линейной системы уравнений. Алгоритм Гаусса дает
оценку O(n3), поэтому рассматриваемая задача полиномиальна.
Пусть формула f(x1,…,xn) имеет конъюнктивную нормальную форму, т.е. имеет вид:
.
Рассмотрим задачу проверки выполнимости для формул КНФ.
В настоящее время неизвестно алгоритма полиномиальной сложности решения данной задачи. Тривиальный алгоритм требует перебор 2n наборов значений переменных и вычисления для каждого из них значения формулы.
NP задачи
Определим теперь класс NP задач распознавания, т.е. имеющих ответ «ДА» или «НЕТ». Для того, чтобы задача I содержалась в классе NP требуется, чтобы если I
имеет ответ “ДА”, существовало бы слово с(I) длины, ограниченной полиномом от размера I, такое, что задача с начальными данными с(I), I принадлежит Р. Слово с(I) называется удостоверением или догадкой для задачи I.
Рассмотрим примеры.
1. Пусть дана задача проверки гамильтоновости бинарного отношения на множестве М={1,2,…,n}. Если R – гамильтоново отношение, то удостоверением этого будет последовательность элементов М: с(R)=i1i2…in. Имея пару с(R), R, можно проверить соотношение (*) и убедиться является ли R – гамильтоновым отношением. Следовательно, задача проверки гамильтоновости бинарного отношения лежит в классе NP.
2. Пусть дана задача проверки выполнимости формул КНФ.
Если f(x1,…,xn) – выполнимая функция, то удостоверением этого будет соответствующий набор 
. Имея пару , f(x1,…,xn), легко убедиться, что f(x1,…,xn) выполнима.
Формализуем эти идеи.
Класс NP определяется через понятие недетерминированного алгоритма. Введем понятие
недетерминированной машины Тьюринга.
Схема недетерминированной машины Тьюринга:
| …… | -3 | -2 | -1 | n | |||||||||||
| * |  x1
| x2 | ……... | xn | ||||||||||
| |||
| |||
Отличие недетерминированной машины Тьюринга от обычной заключается в том,
что недетерминированная машина (НТ) имеет дополнительно угадывающий модуль (УМ), который может только записывать на ленту слова из внешнего алфавита. Поскольку речь идет о задачах распознавания, то удобно считать, что машина имеет два заключительных состояния qY и qN, соответствующие ответам «ДА» и «НЕТ» соответственно. Работа машины имеет две стадии:
1-я стадия – угадывание. В начальный момент на ленте записано слово x=x1…xn – код индивидуальной задачи I, начиная с ячейки 1. В ячейке 0 записан знак раздела *. Угадывающий модуль просматривает ячейку –1. Затем УМ пишет произвольное слово с(х) по одной букве за такт в каждой ячейке с номерами – -1,-2,-3,…. В итоге 1-ой стадии конфигурацией машины будет с(х)*q1x.
2-ая стадия – решение. На этой стадии недетерминированная машина работает как обычная машина Тьюринга с конфигурацией с(х)*q1x. Если машина через конечное число шагов приходит в состояние qY, то говорим, что она принимает конфигурацию с(х)*q1x.
Будем говорить, что недетерминированная машина принимает x, если существует слово с(х), такое что конфигурация с(х)*q1x принимается.
Определим время работы недетерминированной машины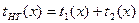 
(если х принимается) где t1(x) – время работы на стадии 1, т.е., по определению, 
;
t2(x) - время работы на стадии 2, т.е., по определению, 
, где tT – время работы обычной машины Тьюринга.
Определим 
Недетерминированная машина НТ решает задачу П за полиномиальное время, если 
для некоторого полинома р.
Временная функция определена только для тех индивидуальных задач х, которые принимаются машиной НТ.
Определим класс задач NP как множество задач, для которых существует недетерминированная машина Тьюринга, принимающая за полиномиальное время те и только те слова, которые соответствуют индивидуальным задачам с ответом «ДА».
Разберем теперь вопрос о взаимоотношении между введенными классами Р и NP. Ясно, что 
. Имеется много причин считать это включение строгим, однако этот факт пока не доказан (1992).
Теорема. Если задача ПÎNP, то существует такой полином р, что П может быть решена детерминированным алгоритмом со сложностью O(2p(n)), где n – размер П.
Выводы.
1. Алгоритм с трудоемкостью O(n) называется линейным. Линейный алгоритм ограниченное число раз просматривает входную информацию и для большинства практических задач является неулучшаемым. Если найден линейный алгоритм для решения задачи, то на этом ее решение заканчивается.
2. Алгоритм, сложность которого равна О(nc), где с – константа называется полиномиальным (класс Р). Говорят, что массовая задача решается эффективно, если существует алгоритм, имеющий полиномиальную сложность. Такая формализация не лишена недостатков. Например, алгоритм имеющий порядок О(n 1000000) вряд ли будет эффективно работать. Но на практике появление какого-нибудь полиномиального алгоритма приводит в конце концов к алгоритму, трудоемкость которого оценивается полиномом небольшой степени. В большинстве случаев эта степень не превосходит 3: O(n3), O(n2), O(n log(n)), 
.
Пример: нахождение кратчайшего маршрута во взвешенном графе.
3. Алгоритм, сложность которого равна О(сn), где 
называется экспоненциальным (класс E).
Пример: задача проверки совпадения булевых функций f(x1,…,xn) и g(x1,…,xn). Решение задачи состоит в составлении таблиц истинности функций с количеством строк 2n.
4. NP-сложные задачи.
Пример: Задача коммивояжера из теории графов. Перебор всех маршрутов в графе из n вершин требует рассмотрения n! вариантов. Но n! растет быстрее, чем 2n.
В недетерминированном алгоритме варианты выбираются случайным образом. Тогда, если повезет, то можно относительно быстро найти вариант, который буде удовлетворять заданным ограничениям. Такие задачи, имеющие недетерминированное решение, которое иногда удается найти за полиномиальное время и называют NP сложными.
Существует мнение, что детерминированных алгоритмов решения таких задач не существует. NP сложные задачи не имеют гарантированных оценок времени решения. Даже незначительное изменение исходных данных приводит к резкому увеличению времени решения.
Примеры.
1. Выполнимость. Дана КНФ, представляющая булеву функцию. Выяснить является ли она выполнимой.
2. Клика. Определить содержит ли граф клику мощности К.
3. Независимость. Определить содержит ли граф независимое множество из К вершин.
4. Ядро графа.
5. Гамильтонов цикл.
6. Раскраска графа. Определить существует ли правильная раскраска графа посредством К цветов.
Имеется ряд задач, входящих в NP класс, для решения которых не найдено полиномиальных алгоритмов.
